【力扣刷题】神奇字符串

神奇字符串

🔗 题目链接

题目描述

神奇字符串 s 仅由 '1' 和 '2' 组成，并需要遵守下面的规则：

• 神奇字符串 s 的神奇之处在于，串联字符串中 '1' 和 '2' 的连续出现次数可以生成该字符串。

s 的前几个元素是 s = "1221121221221121122……" 。如果将 s 中连续的若干 1 和 2 进行分组，可以得到 "1 22 11 2 1 22 1 22 11 2 11 22 ......" 。每组中 1 或者 2 的出现次数分别是 "1 2 2 1 1 2 1 2 2 1 2 2 ......" 。上面的出现次数正是 s 自身。

给你一个整数 n ，返回在神奇字符串 s 的前 n 个数字中 1 的数目。

题目分析

这道题最先想到的方法就是，把这个长度为n的字符串构造出来，这样就能够计算出1的数目了。

如果 n<4，那么不用计算，就可以知道返回1。

接下来，我们从第 4 个位置开始构造（i初始值为4）:

• 第 4 个位置的数字是由第 3 个位置（i-1）决定的，因为最后一次是 2，所以第 4 个位置开始要插入 1；
• 第 4 个位置开始插入 1，插入的次数有第 3 个位置决定的（j初始值为3）；

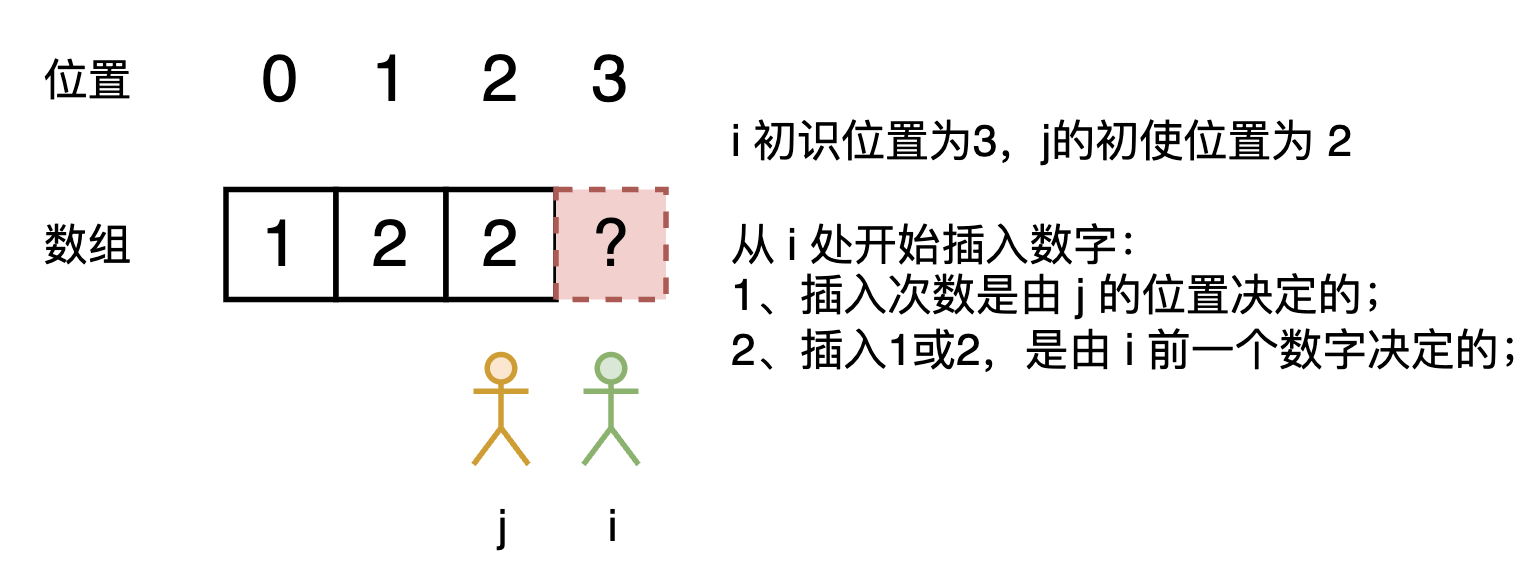
按照这样的顺序来构造处字符串 s，在构造的同时，我们来计算 1 出现的次数即可，直到构造的字符串长度等于 n。

题解代码

/**
 * @param {number} n
 * @return {number}
 */
var magicalString = function (n) {
  let num = 1;
  if (n < 4) return num;
  let s = [1, 2, 2];
  let i = 3,
    j = 2,
    temp = 0,
    isOne = true;
  while (i < n) {
    isOne = s[i - 1] == 2;
    for (temp = 0; temp < s[j]; temp++) {
      if (isOne) {
        s.push(1);
        num++;
      } else {
        s.push(2);
      }
      i++;
      if (i >= n) break;
    }
    j++;
  }
  return num;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

运行结果