【降维之PCA】PCA实例

数据介绍：
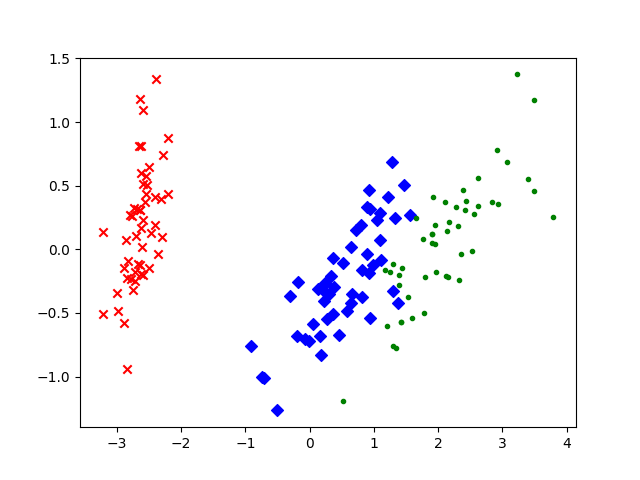
PCA实现高维数据可视化目标:已知莺尾花数据是4维的，共三类样本(150*4)。使用 РСA实现鸢尾花数据进行降维，实现在二维平面上的可视化。

PCA可以将具有相关性的高维变量合成为线性无关的低维变量，成为主成分，主成分能够尽可能的保留原始数据的信息
矩阵的主成分就是其协方差矩阵对应的特征向量，按照对应特征值大小排序，最大特征值为第一主成分，以此类推

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
 
data=load_iris()
y=data.target #使用y表示数据集中的标签
x=data.data #使用x表示数据集中的属性数据
pca=PCA(n_components=2) #加载PCA算法，设置降维后主成分数目为2
reduced_X=pca.fit_transform(x) #对原始数据进行降维
#下面按类别对降维后的数据进行保存
red_x, red_y = [], []                       #第一类数据点
blue_x, blue_y = [], []                     #第二类数据点
green_x, green_y = [], []                   #第三类数据点
 
 
for i in range(len(reduced_X)):             #按照鸢尾花的类别将降维后的数据点保存在不同的列表中
    if y[i] == 0:
        red_x.append(reduced_X[i][0])
        red_y.append(reduced_X[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_X[i][0])
        blue_y.append(reduced_X[i][1])
    else:
        green_x.append(reduced_X[i][0])
        green_y.append(reduced_X[i][1])
 
plt.scatter(red_x, red_y, c='r', marker='x')     #第一类数据点散点图
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()