【CV】第 4 章：图像深度学习

   🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​

📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

文章目录

了解 CNN 及其参数

Convolution（卷积）

Convolution over volume – 3 x 3 filter（体积上的卷积 - 3 x 3 过滤器）

Convolution over volume – 1 x 1 filter（体积上的卷积 - 1 x 1 过滤器）

Pooling （池化）

Padding（填充）

Stride（跨步）

Activation（激活）

Fully connected layers（全连接层）

正则化

Dropout

内部协方差偏移和批量归一化

Softmax

优化 CNN 参数

基准案例

迭代 1 – CNN 参数调整

迭代 2 – CNN 参数调整

迭代 3 – CNN 参数调整

迭代 4 – CNN 参数调整

可视化神经网络的层

构建自定义图像分类器模型并可视化其层

神经网络输入和参数

输入图像

定义训练和验证生成器

开发模型

编译和训练模型

输入测试图像并将其转换为张量

可视化第一层激活

可视化多层激活

训练现有的高级图像分类器模型并可视化其层

概括

在本章中，您将了解如何使用边缘检测在体积上创建卷积操作，以及不同的卷积参数，如滤波器大小、尺寸和操作类型（卷积与池化）如何影响卷积体积（宽度与深度）。本章将非常详细地概述神经网络如何看待图像以及它如何使用该可视化来对图像进行分类。您将从构建您的第一个神经网络开始，然后在图像通过不同层时对其进行可视化。然后，您将网络模型的准确性和可视化与 VGG 16 或 Inception 等高级网络进行比较。

在本章中，我们将介绍以下主题：

• 了解 CNN 及其参数
• 优化 CNN 参数
• 可视化神经网络的层

了解 CNN 及其参数

卷积神经网络( CNN ) 是一种自学习网络，它通过观察不同类别的图像对类似于我们人类大脑学习方式的图像进行分类。CNN 通过应用图像过滤和处理各种过滤器大小、数量和非线性操作的方法来学习图像的内容。这些过滤器和操作应用于许多层，以便每个后续层的空间维度在图像转换过程中减小，并且它们的深度增加。

对于每个过滤应用程序，学习内容的深度都会增加。这从边缘检测开始，然后是识别形状，然后是称为特征的形状集合，等等。在我们如何理解信息方面，这类似于人脑。例如，在阅读理解测试中，我们需要回答关于一篇文章的五个问题，每个问题都可以被视为一个需要从文章中获得特定信息的类：

1. 首先，我们略读整个段落，这意味着空间维度是完整的段落，深度（我们对段落的理解）是低的，因为我们只是略过它。
2. 接下来，我们略读问题以了解每个类（问题）的特征——即在文章中寻找什么。在 CNN 中，这相当于考虑使用什么卷积和池化操作来提取特征。
3. 然后，我们阅读文章的特定部分，找到与课程相似的内容，并深入研究这些部分——这里，空间维度低，但深度高。我们重复这个过程两到三遍来回答所有的问题。我们继续增加我们的理解深度，并更加专注于特定领域（缩小维度），直到我们有一个很好的理解。在一个 CNN 中，这相当于逐渐增加深度和缩小维度——卷积操作通过改变过滤器的数量来改变深度；池化缩小了维度。
4. 为了节省时间，我们倾向于跳过段落来查找与答案匹配的相关段落。在卷积中，这相当于步幅，它缩小了维度但不改变深度。
5. 下一个过程是将问题与文章中的答案进行匹配。我们通过在心理上调整问题的答案来做到这一点。在这里，我们不会更深入- 我们将问题和答案放在一起，以便我们可以匹配它们。在 CNN 中，这相当于展平并使用全连接层。

1. 在此过程中，我们可能有多余的信息——我们将其删除，以便我们只能获得与文章中的问题相关的信息。在 CNN 中，这相当于 dropout。
2. 最后一个阶段实际上是进行匹配练习以回答问题。在 CNN 中，这相当于 Softmax 操作。

CNN 的图像过滤和处理方法包括做各种各样的事情，所有这些事情都是通过使用以下方式进行的：

• Convolution (Conv2D)
• Convolution over volume – 3 x 3 filter
• Convolution over volume – 1 x 1 filter
• Pooling
• Padding
• Stride
• Activation
• Fully connected layer
• Regularization
• Dropout
• Internal covariance shift and batch normalization
• Softmax

下图说明了 CNN 及其组件：

让我们回顾一下每个组件的功能。

Convolution（卷积）

卷积是 CNN 的主要组成部分。它包括将图像的一部分与内核（过滤器）相乘以产生输出。卷积的概念在第 1 章“计算机视觉和 TensorFlow 基础”中进行了简要介绍。请参阅该章节以了解基本概念。卷积操作是通过在输入图像上滑动内核来执行的。在每个位置，都会执行逐元素矩阵乘法，然后是乘法范围内的累积和。

在每次卷积操作之后，CNN 会更多地了解图像——它首先学习边缘，然后是下一次卷积中的形状，然后是图像的特征。在卷积操作期间，滤波器大小和滤波器数量可以改变。通常，在特征图的空间维度通过卷积、池化和跨步操作减少后，过滤器的数量会增加。特征图的深度随着滤波器尺寸的增加而增加。下图解释了当我们有两个不同的内核选择用于边缘检测时的 Conv2D：

上图显示了以下要点：

• 如何通过在输入图像上滑动 3 x 3 窗口来执行卷积操作。
• 逐元素矩阵乘法和求和结果，用于生成特征图。
• 多个特征图堆叠为多个卷积操作生成最终输出。

Convolution over volume – 3 x 3 filter（体积上的卷积 - 3 x 3 过滤器）

在前面的示例中，我们在二维图像（灰度）上应用了 3 x 3 卷积。在本节中，我们将学习如何通过使用卷积运算的 3 x 3 边缘滤波器来转换具有三个通道（红色、绿色和蓝色( RGB )）的三维图像。下图以图形方式显示了这种转换：

上图显示了如何使用 3 x 3 过滤器（边缘检测器）在宽度减少和深度增加（从 3 到 32）方面转换 7 x 7 图像图形的一部分。内核 ( f i )中的 27 (3 x 3 x 3) 个单元中的每一个都乘以输入 ( A i ) 的相应 27 个单元。然后，将这些值与整流线性单元( ReLU ) 激活函数 ( bi )相加，形成单个元素 ( Z )，如以下等式所示：

通常，在卷积层中，有许多过滤器执行不同类型的边缘检测。在前面的示例中，我们有 32 个过滤器，这会产生 32 个不同的堆栈，每个堆栈由 5 x 5 层组成。

在本书的其余部分，3 x 3 滤波器将广泛用于神经网络开发。例如，你会在 ResNet 和 Inception 层看到大量使用它，我们将在第 5 章，神经网络架构和模型中讨论。32 个大小为 3 x 3 的过滤器可以在 TensorFlow 中表示为.tf.keras.layers.Conv2D(32, (3,3)). 在本章后面，您将了解如何将这种卷积与 CNN 的其他层一起使用。

Convolution over volume – 1 x 1 filter（体积上的卷积 - 1 x 1 过滤器）

在本节中，我们将了解 1 x 1 卷积的重要性及其用例。一个 1 x 1 的卷积滤波器是图像的直接倍数，如下图所示：

在上图中，1 x 1 卷积滤波器值 1 用于上一节的 5 x 5 图像输出，但实际上它可以是任何数字。在这里，我们可以看到使用 1 x 1 过滤器保留了它的高度和宽度，而深度增加了过滤器通道的数量。这是 1 x 1 滤波器的基本优势。三维内核 ( fi ) 中的三个 (1 x 1 x 3) 单元中的每一个都乘以输入 ( A i )的相应三个单元。然后，将这些值与 ReLU 激活函数(bi )相加，形成单个元素 ( Z )：

上图显示了 1 x 1 过滤器导致深度增加，而相同的 1 x 1 过滤器可用于使值减小，如下图所示：

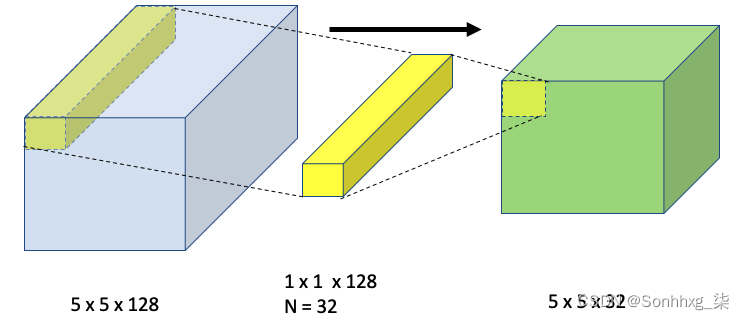
上图显示了 1 x 1 x 128 图像过滤器如何将卷积深度减少到 32 个通道。

本书将使用 1 x 1 卷积。稍后，您将了解到池化减小了宽度，而 1 x 1 卷积保留了宽度，但可以根据需要收缩或扩展深度。例如，您将看到在网络和Inception 层中使用了 1 x 1 卷积（在第 5 章，神经网络架构和模型中）。具有 1 x 1 卷积大小的 32 滤波器可以在 TensorFlow 中表示为.tf.keras.layers.Conv2D(32, (1,1))。

Pooling （池化）

池化是卷积之后的下一个操作。它用于在不改变深度的情况下降低维度和特征图大小（宽度和高度）。轮询的参数数量为零。两种最流行的池化类型如下：

• 最大池化
• 平均池化

在最大池化中，我们将窗口滑过特征图并取窗口的最大值，而在平均池化中，我们取窗口中的平均值。卷积层和池化层一起执行特征提取任务。下图显示了在 7 x 7 图像上使用的最大池化操作和平均池化操作：

请注意 3 x 3 窗口如何因池化而缩小（如绿线所示）为单个值，从而导致 5 x 5 矩阵维度变为 3 x 3 矩阵。

Padding（填充）

填充用于保留特征图的大小。使用卷积，可能会出现两个问题，而填充解决了这两个问题：

• 特征图的大小随着每次卷积操作而缩小。例如，在上图中，一个 7 x 7 的特征图由于卷积而缩小到 5 x 5。
• 边缘的信息丢失了，因为边缘的像素只改变了一次，而中间的像素被许多卷积操作改变了很多次。

下图显示了在 7 x 7 输入图像上使用的大小为 1 的填充操作：

请注意填充如何保存维度，以便输出与输入的大小相同。

Stride（跨步）

通常，在卷积中，我们将内核移动一步，将卷积应用于该步骤，依此类推。步幅允许我们跳过一步。让我们来看看：

• 当 stride = 1 时，我们应用正常卷积而不跳过。
• 当 stride = 2 时，我们跳过一步。这会将图像尺寸从 7 x 7 减小到 3 x 3（参见下图）：

在这里，每个 3 x 3 窗口显示跳过一步的结果。跨步的结果是缩小维度，因为我们跳过了潜在的 x ， y 位置。

Activation（激活）

激活层为神经网络增加了非线性。这一点至关重要，因为图像中的图像和特征是高度非线性问题，而 CNN 中的大多数其他功能（Conv2D、池化、全连接层等）仅生成线性变换。激活函数在将输入值映射到其范围时产生非线性。如果没有激活函数，无论添加多少层，最终结果仍然是线性的。

使用了许多类型的激活函数，但最常见的如下：

• Sigmoid
• Tanh
• ReLU

前面的激活函数如下图所示：

每个激活函数都表现出非线性行为，当输入大于 3 时， Sigmoid和Tanh接近 3，而ReLU继续增加。

下图显示了不同激活函数对输入大小的影响：

ReLU 激活函数相对于 Tanh 和 Sigmoid 激活函数具有以下优点：

• 与 ReLU 相比，Sigmoid 和 Tanh 存在梯度消失问题（学习速度慢），因为它们在输入值大于 3 时都接近 1。
• Sigmoid 激活函数仅对小于 0 的输入值具有正值。
• ReLU 函数对计算很有效。

Fully connected layers（全连接层）

全连接层，也称为密集层，通过对当前层中的每个连接的神经元和前一层中的每个连接的神经元施加权重和偏置，将它们连接起来。权重和偏差的向量称为过滤器。这可以用以下等式表示：

如卷积部分所述，滤波器可以采用边缘滤波器的形式来检测边缘。在神经网络中，许多神经元共享相同的过滤器。权重和过滤器允许全连接层充当分类器。

正则化

正则化是一种用于减少过拟合的技术。它通过向模型误差函数（模型输出-训练值）添加一个附加项来实现这一点，以防止模型权重参数在训练期间取极值。CNN 中使用了三种类型的正则化：

• L1 正则化：对于每个模型权重w，一个附加参数λ | w |, 被添加到模型目标中。这种正则化使优化期间的权重因子变得稀疏（接近于零）。
• L2 正则化：对于每个模型权重w，一个附加参数1/2λ w 2被添加到模型目标中。这种正则化使权重因子在优化过程中扩散。L2 正则化有望提供优于 L1 正则化的性能。
• 最大范数约束：这种类型的正则化为 CNN 的权重添加了一个最大界限，因此 | w | < c，其中c可以是 3 或 4。最大范数约束可防止神经网络过度拟合，即使学习率很高。

Dropout

Dropout是一种特殊类型的正则化，是指忽略神经网络中的神经元。dropout = 0.2 的全连接层意味着只有 80% 的全连接神经元连接到下一层。神经元在当前步骤被丢弃，但在下一步处于活动状态。Dropout 可以防止网络依赖少量的神经元，从而防止过拟合。Dropout 应用于输入神经元，但不应用于输出神经元。下图显示了有和没有 dropout 的神经网络：

以下是dropout的优点：

• Dropout 迫使神经网络学习更稳健的特征。
• 每个 epoch 的训练时间更少，但迭代次数增加了一倍。
• Dropout 可以提高准确率——大约 1% 到 2%。

内部协方差偏移和批量归一化

在训练过程中，每一层输入的分布随着前一层权重因子的变化而变化，从而导致训练速度变慢。这是因为它需要较低的学习率和权重因子选择。Sergey Ioffe 和 Christian Szegedy在他们题为Batch Normalization: Accelerated Deep Network Training by Reducing Internal Co-variance Shift的论文中称这种现象为内部协方差偏移。详情请参考：https ://arxiv.org/abs/1502.03167 。

批标准化通过从当前输入中减去前一层的批均值并将其除以批标准差来解决协方差偏移的问题。然后将这个新输入乘以当前权重因子并加上偏置项以形成输出。下图显示了神经网络的中间输出函数，有和没有批量归一化：

当应用批量归一化时，我们计算大小为m的整个小批量的均值 ( μ ) 和方差 ( σ ) 。然后，利用这些信息，我们计算归一化的输入。小批量的输出计算为比例 ( γ ) 乘以归一化输入，再加上偏移量 ( β )。在 TensorFlow 中，这可以表示如下。除方差 epsilon 之外的所有项都已在上图中进行了解释，它是归一化输入计算中的ε项，以避免除以零：

tf.nn.batch_normalization(x,mean,variance,offset,scale,variance_epsilon,name=None)

麻省理工学院的 Shibani Santurkar、Dimitris Tsipras、Andrew Ilyas 和 Aleksander Madry 在他们题为“批标准化如何帮助优化？ ”的论文中详细解释了批标准化的优势。. 论文的详细信息可以在https://arxiv.org/abs/1805.11604找到。

该论文的作者发现批量归一化不会减少内部协方差偏移。批量归一化中的学习速度可归因于由于使用归一化输入而不是常规输入数据而导致的输入的平滑度，常规输入数据可能由于扭结、锐边和局部最小值或最大值而有很大的变化。这使得梯度下降算法更加稳定，从而允许它使用更大的步长来更快地收敛。这确保它不会遇到任何错误。 

Softmax

Softmax 是一种激活函数，用于 CNN 的最后一层。它由以下等式表示，其中P是每个类的概率，n是类的总数：

下表显示了使用前面描述的 Softmax 函数时七个类别中每个类别的概率：

这用于计算每个类的分布概率。

优化 CNN 参数

CNN 有许多不同的参数。训练 CNN 模型需要许多输入图像并执行处理，这可能非常耗时。如果选择的参数不是最优的，则必须再次重复整个过程。这就是为什么了解每个参数的功能及其相互关系很重要的原因：以便在运行 CNN 之前优化它们的值，以最大限度地减少重复运行。CNN的参数如下：

• 图像大小 = ( nxn )
• 过滤器 = (f h ,f w )，f h = 应用于图像高度的过滤器，f w = 应用于图像宽度的过滤器
• 过滤器数量 = n f
• 填充 = p
• 步幅 = s
• 输出大小= {(n + 2p - f)/s +1} x {(n + 2p - f)/s + 1}
• 参数数量= (f h xf w + 1)xn f

关键任务是为每一层选择上述参数（过滤器大小（f）、过滤器数量（nf ）、每层中的步幅（s ）、填充值（ p）、激活值（a）和偏差）。美国有线电视新闻网。下表显示了各种 CNN 参数的特征图：

上表各参数说明如下：

• 输入图像：第一个输入层是大小为(48 x 48)的灰度图像，因此深度为1。特征图大小 = 48 x 48 x 1 = 2,304。它没有参数。
• 第一个卷积层：CONV1 ( filter shape =5*5, stride=1 ) layer's height, width = (48-5+1) =44 , feature map size = 44 x 44 x 64 = 123904 , and number of parameters = (5 x 5 + 1) x 64 = 1,664。
• 第一个池化层（POOL1）：池化层没有参数。
• 剩余的卷积层和池化层：剩余的计算——CONV2 、CONV3、CONV4、CONV5、POOL2—— 遵循与第一个卷积层相同的逻辑。
• 全连接（FC）层：对于全连接层（FC1，FC2），参数数量 = [（当前层 n * 前一层 n）+ 1] 参数 = 128 * 1,024 + 1 = 131,073。
• Dropout (DROP)：对于 dropout，有 20% 的神经元被丢弃。剩余的神经元 = 1,024 * 0.8 = 820。第二个 dropout 的参数数量 = 820 x 820 + 1 = 672,401。
• CNN 的最后一层总是 Softmax：对于 Softmax，参数的数量 = 7 x 820 + 1 = 5,741。

第 3 章面部表情识别的第一张图所示的神经网络类，使用 OpenCV 和 CNN 进行面部检测有 7 个类，其准确率约为 54%。

在以下部分中，我们将使用 TensorFlow 输出来优化各种参数。我们从基线案例开始，然后通过调整此处描述的参数尝试五次迭代。这个练习应该让你很好地理解 CNN 的参数以及它们如何影响最终模型的输出。

基准案例

基线情况由神经网络的以下参数表示：

• Number of instances: 35,888
• Instance length: 2,304
• 28,709 train samples
• 3,589 test samples

模型迭代如下：

Epoch 1/5
 256/256 [=======================] - 78s 306ms/step - loss: 1.8038 - acc: 0.2528
 Epoch 2/5
 256/256 [=======================] - 78s 303ms/step - loss: 1.6188 - acc: 0.3561
 Epoch 3/5
 256/256 [=======================] - 78s 305ms/step - loss: 1.4309 - acc: 0.4459
 Epoch 4/5
 256/256 [=======================] - 78s 306ms/step - loss: 1.2889 - acc: 0.5046
 Epoch 5/5
 256/256 [=======================] - 79s 308ms/step - loss: 1.1947 - acc: 0.5444

接下来，我们将优化 CNN 参数，以确定哪些参数在改变精度时影响最大。我们将在四次迭代中运行这个实验。

迭代 1 – CNN 参数调整

去掉一个 Conv2D 64 和一个 Conv2D 128，这样 CNN 就只有一个 Conv2D 64 和一个 Conv2D 128 了：

Epoch 1/5
 256/256 [========================] - 63s 247ms/step - loss: 1.7497 - acc: 0.2805
 Epoch 2/5
 256/256 [========================] - 64s 248ms/step - loss: 1.5192 - acc: 0.4095
 Epoch 3/5
 256/256 [========================] - 65s 252ms/step - loss: 1.3553 -acc: 0.4832
 Epoch 4/5
 256/256 [========================] - 66s 260ms/step - loss: 1.2633 - acc: 0.5218
 Epoch 5/5
 256/256 [========================] - 65s 256ms/step - loss: 1.1919 - acc: 0.5483

结果：删除 Conv2D 层不会对性能产生不利影响，但也不会使其变得更好。

接下来，我们将保留此处所做的更改，但我们会将平均池化转换为最大池化。

迭代 2 – CNN 参数调整

删除一个 Conv2D 64 和一个 Conv2D 128，这样 CNN 就只有一个 Conv2D 64 和一个 Conv2D 128 进行此更改。此外，将平均池转换为最大池，如下所示：

Epoch 1/5
 256/256 [========================] - 63s 247ms/step - loss: 1.7471 - acc: 0.2804
 Epoch 2/5
 256/256 [========================] - 64s 252ms/step - loss: 1.4631 - acc: 0.4307
 Epoch 3/5
 256/256 [========================] - 66s 256ms/step - loss: 1.3042 - acc: 0.4990
 Epoch 4/5
 256/256 [========================] - 66s 257ms/step - loss: 1.2183 - acc: 0.5360
 Epoch 5/5
 256/256 [========================] - 67s 262ms/step - loss: 1.1407 - acc: 0.5691

结果：同样，此更改对准确性没有显着影响。

接下来，我们将显着减少隐藏层的数量。我们将更改输入层并完全移除第二个 Conv2D 和相关的池化。在第一个 Conv2D 之后，我们将直接转到第三个 Conv2D。

迭代 3 – CNN 参数调整

第二个卷积层被完全丢弃；输入层从 5 x 5 更改为 3 x 3：

model.add(Conv2D(64, (3, 3), activation='relu', input_shape=(48,48,1)))

第三个卷积层保持不变。这一层如下：

model.add(Conv2D(128, (3, 3), activation='relu')) 
model.add(AveragePooling2D(pool_size=(3,3), strides=(2, 2)))

致密层没有变化。其输出如下：

Epoch 1/5
 256/256 [==========================] - 410s 2s/step - loss: 1.6465 - acc: 0.3500
 Epoch 2/5
 256/256 [==========================] - 415s 2s/step - loss: 1.3435 - acc: 0.4851
 Epoch 3/5
 256/256 [==========================] - 412s 2s/step - loss: 1.0837 - acc: 0.5938
 Epoch 4/5
 256/256 [==========================] - 410s 2s/step - loss: 0.7870 - acc: 0.7142
 Epoch 5/5
 256/256 [==========================] - 409s 2s/step - loss: 0.4929 - acc: 0.8242

结果：计算时间很慢，但准确率最高，即82%。

迭代 4 – CNN 参数调整

在本次迭代中，所有参数都与上一次迭代中相同，除了strides = 2，它是在第一个 Conv2D 之后添加的。

接下来，我们保持一切不变，但在第一个 Conv2D 之后添加一个池化层：

在此迭代中，对密集层没有任何更改。计算时间更快但精度下降：

Epoch 1/5
 256/256 [========================] - 99s 386ms/step - loss: 1.6855 - acc: 0.3240
 Epoch 2/5
 256/256 [========================] - 100s 389ms/step - loss: 1.4532 - acc: 0.4366
 Epoch 3/5
 256/256 [========================] - 102s 397ms/step - loss: 1.3100 - acc: 0.4958
 Epoch 4/5
 256/256 [=======================] - 103s 402ms/step - loss: 1.1995 - acc: 0.5451
 Epoch 5/5
 256/256 [=======================] - 104s 407ms/step - loss: 1.0831 - acc: 0.5924

结果类似于我们在基线迭代中得到的结果，即 1 和 2。

从这个实验中，我们可以得出以下关于 CNN 参数优化的结论：

• 减少 Conv2D 的数量并消除一个 strides = 2的池化层具有最显着的效果，因为它提高了准确度（大约 30%）。然而，这是以牺牲速度为代价的，因为 CNN 的大小并没有减少。
• 池化类型（平均池化与最大池化）对测试准确性的影响微乎其微。

产生最佳精度的 CNN 架构如下：

请注意，与原始架构相比，此架构要简单得多。在下一章中，您将了解一些最先进的卷积模型以及使用它们的原因。然后，我们将回到这个优化问题，学习如何更有效地选择参数以实现更好的优化。

可视化神经网络的层

在本章中，我们了解了如何将图像转换为边缘然后转换为特征图，并且通过这样做，神经网络能够通过组合许多特征图来预测类别。在前几层，神经网络将线条和角可视化，而在最后几层，神经网络识别复杂的模式，例如特征图。这可以分为以下几类。

• 构建自定义图像分类器模型并可视化其层
• 训练现有的高级图像分类器模型并可视化其层

让我们来看看这些类别。

构建自定义图像分类器模型并可视化其层

在本节中，我们将开发自己的家具分类器网络。这将包括三类：沙发、床和椅子。基本过程描述如下。

此示例的详细代码可以在 GitHub 上找到：https ://github.com/PacktPublishing/Mastering-Computer-Vision-with-TensorFlow-2.0/blob/master/Chapter04/Chapter4_classification_visualization_custom_model%26VGG.ipynb 。

from __future__ import absolute_import, division, print_function, unicode_literals,
import tensorflow as tf,
from tensorflow.keras.applications import VGG16\n
from keras.applications.vgg16 import preprocess_input,
  
from keras import models
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Conv2D, Flatten, Dropout, GlobalAveragePooling2D, MaxPooling2D
from tensorflow.keras.preprocessing.image import ImageDataGenerator\n",
from tensorflow.keras.optimizers import SGD, Adam
import os
import numpy as np
import matplotlib.pyplot as plt

train_dir = 'furniture_images/train' 
train_bed_dir = os.path.join(train_dir, 'bed') 
num_bed_train = len(os.listdir(train_bed_dir))

train_datagen = ImageDataGenerator(preprocessing_function=preprocess_input,rotation_r

model = Sequential([Conv2D(96, 11, padding='valid', activation='relu',input_shape(img_height, img_width,3)), 
MaxPooling2D(),
Dropout(0.2),
Conv2D(256, 5, padding ='same', activation='relu'),
MaxPooling2D(),
Conv2D(384, 3, padding='same', activation='relu'),
Conv2D(384, 3, padding='same', activation=' relu'), 
Conv2D(256, 3, padding='same', activation='relu'),
MaxPooling2D(), 
Dropout(0.2),
Conv2D(1024, 3, padding='same', activation='relu'), 
MaxPooling2D(),
Dropout(0.2),
Flatten(),
Dense(4096, activation='relu'), 
Dense(3)])

model.compile(optimizer='adam',loss=tf.keras.losses.BinaryCrossentropy(from_logits=True), metrics=['accuracy']) 
 
history = model.fit(train_generator,epochs=NUM_EPOCHS,steps_per_epoch=num_train_images // batchsize,validation_data=val_generator, validation_steps=num_val_images // batchsize)

WARNING:tensorflow:sample_weight modes were coerced from
 ...
 to
 ['...']
 Train for 10 steps, validate for 1 steps
 Epoch 1/10
 10/10 [==============================] - 239s 24s/step - loss: 13.7108 - accuracy: 0.6609 - val_loss: 0.6779 - val_accuracy: 0.6667
 Epoch 2/10
 10/10 [==============================] - 237s 24s/step - loss: 0.6559 - accuracy: 0.6708 - val_loss: 0.5836 - val_accuracy: 0.6693
 Epoch 3/10
 10/10 [==============================] - 227s 23s/step - loss: 0.5620 - accuracy: 0.7130 - val_loss: 0.5489 - val_accuracy: 0.7266
 Epoch 4/10
 10/10 [==============================] - 229s 23s/step - loss: 0.5243 - accuracy: 0.7334 - val_loss: 0.5041 - val_accuracy: 0.7292
 Epoch 5/10
 10/10 [==============================] - 226s 23s/step - loss: 0.5212 - accuracy: 0.7342 - val_loss: 0.4877 - val_accuracy: 0.7526
 Epoch 6/10
 10/10 [==============================] - 226s 23s/step - loss: 0.4897 - accuracy: 0.7653 - val_loss: 0.4626 - val_accuracy: 0.7604
 Epoch 7/10
 10/10 [==============================] - 227s 23s/step - loss: 0.4720 - accuracy: 0.7781 - val_loss: 0.4752 - val_accuracy: 0.7734
 Epoch 8/10
 10/10 [==============================] - 229s 23s/step - loss: 0.4744 - accuracy: 0.7508 - val_loss: 0.4534 - val_accuracy: 0.7708
 Epoch 9/10
 10/10 [==============================] - 231s 23s/step - loss: 0.4429 - accuracy: 0.7854 - val_loss: 0.4608 - val_accuracy: 0.7865
 Epoch 10/10
 10/10 [==============================] - 230s 23s/step - loss: 0.4410 - accuracy: 0.7865 - val_loss: 0.4264 - val_accuracy: 0.8021

img_path = 'furniture_images/test/chair/testchair.jpg' 
img = image.load_img(img_path, target_size=(150, 150)) 
img_tensor = image.img_to_array(img) 
img_tensor = np.expand_dims(img_tensor, axis=0) 
img_tensor = preprocess_input(img_tensor)
featuremap = model.predict(img_tensor)

layer_outputs = [layer.output for layer in model.layers[:16]] 
activation_modelfig = Model(inputs=model.input, outputs=layer_outputs) 
activationsfig = activation_modelfig.predict(img_tensor)

model = Model(inputs=[a1, a2], outputs=[b1, b2, b3])

first_layer_activation = activationsfig[0] 
print(first_layer_activation.shape) 
plt.matshow(first_layer_activation[0, :, :, 95], cmap='viridis')

for i in range(0,12):
    current_layer_activation = activationsfig[i]
    ns = current_layer_activation.shape[-1]
    plt.imshow(current_layer_activation[0, :, :, 0], cmap='viridis')
    plt.imshow(current_layer_activation[0, :, :, int(ns/2)], cmap='viridis')
    plt.imshow(current_layer_activation[0, :, :, ns-1], cmap='viridis')

Epoch 1/10
 135/135 [==============================] - 146s 1s/step - loss: 1.8203 - accuracy: 0.4493 - val_loss: 0.6495 - val_accuracy: 0.7000
 Epoch 2/10
 135/135 [==============================] - 151s 1s/step - loss: 1.2111 - accuracy: 0.6140 - val_loss: 0.5174 - val_accuracy: 0.8067
 Epoch 3/10
 135/135 [==============================] - 151s 1s/step - loss: 0.9528 - accuracy: 0.6893 - val_loss: 0.4765 - val_accuracy: 0.8267
 Epoch 4/10
 135/135 [==============================] - 152s 1s/step - loss: 0.8207 - accuracy: 0.7139 - val_loss: 0.4881 - val_accuracy: 0.8133
 Epoch 5/10
 135/135 [==============================] - 152s 1s/step - loss: 0.8057 - accuracy: 0.7355 - val_loss: 0.4780 - val_accuracy: 0.8267
 Epoch 6/10
 135/135 [==============================] - 152s 1s/step - loss: 0.7528 - accuracy: 0.7571 - val_loss: 0.3842 - val_accuracy: 0.8333
 Epoch 7/10
 135/135 [==============================] - 152s 1s/step - loss: 0.6801 - accuracy: 0.7705 - val_loss: 0.3370 - val_accuracy: 0.8667
 Epoch 8/10
 135/135 [==============================] - 151s 1s/step - loss: 0.6716 - accuracy: 0.7906 - val_loss: 0.4276 - val_accuracy: 0.8800
 Epoch 9/10
 135/135 [==============================] - 152s 1s/step - loss: 0.5954 - accuracy: 0.7973 - val_loss: 0.4608 - val_accuracy: 0.8533
 Epoch 10/10
 135/135 [==============================] - 152s 1s/step - loss: 0.4926 - accuracy: 0.8152 - val_loss: 0.3550 - val_accuracy: 0.8933