机器学习入门（二）一元线性回归

目录

2.一元线性回归 

2.1 什么是线性回归

2.2 代价函数

2.2.1 假设函数

2.2.2 代价函数 

2.3 梯度下降法 

2.3.1 引出问题

2.3.2 梯度下降法

2.3.3 梯度下降法的缩放因子对梯度下降法的影响

---

2.一元线性回归 

2.1 什么是线性回归

        单元线性回归是拟合一条线，将训练数据尽可能分布到线上。如下图：是一个监督学习（因为给定正确答案对于每一个输入变量：每一个面积对应一个房价）

        我们要解决的问题是拟定一个线性函数使尽可能多的点在直线上并使代价函数最低（后面说），并给出一个新的输入用这条直线进行拟合时能得到尽量满意的结果。

        另外多变量的线性回归称为多元线性回归（比如房价不仅仅受房子面积大小影响，房龄、地段等等）

      简单来说，用训练集去预测房价

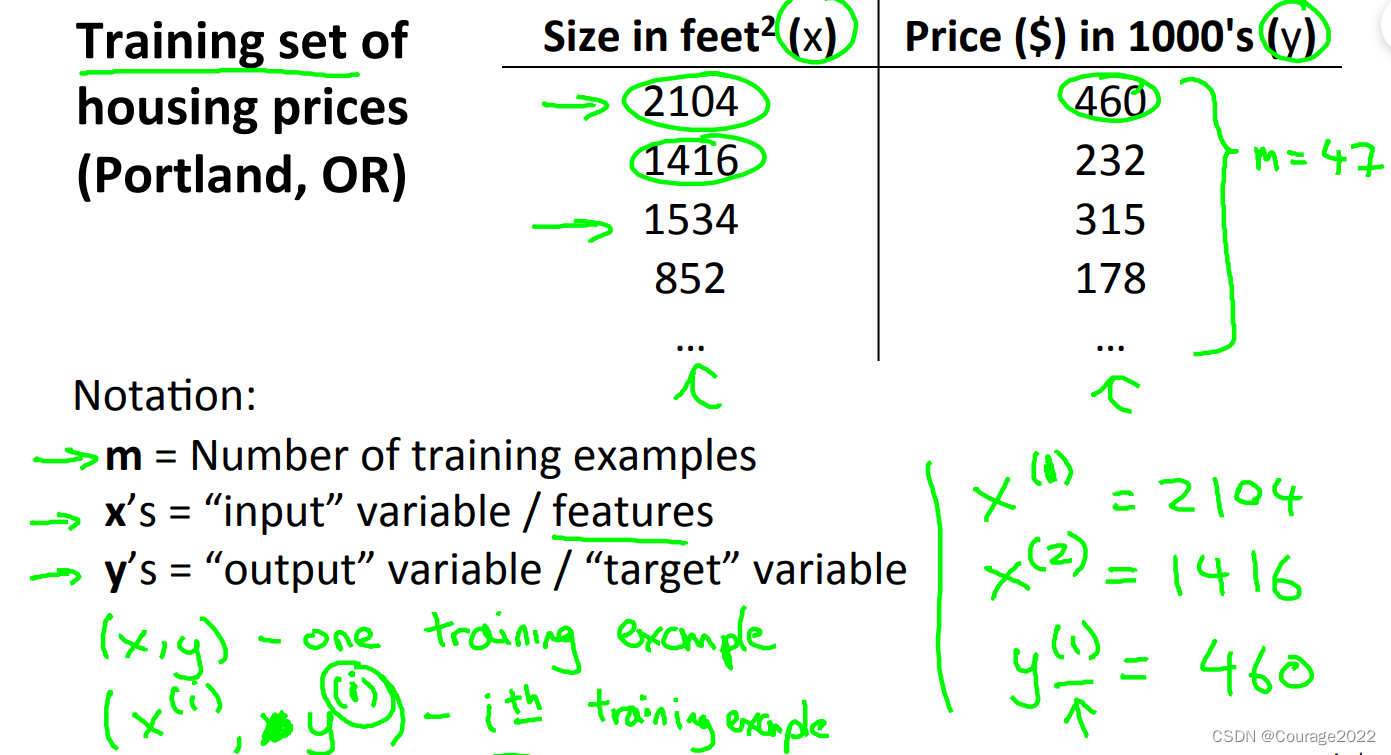
      我们定义为训练集的数量（多少组数据），是输入变量（特征：这个例子指房子大小），是输出变量（目标变量：这里指输入特征下的预测结果）；

      同时用表示一个训练样本，表示训练集的第i个样本。

2.2 代价函数

2.2.1 假设函数

        我们如何评价一个机器学习的好坏？先看下图！

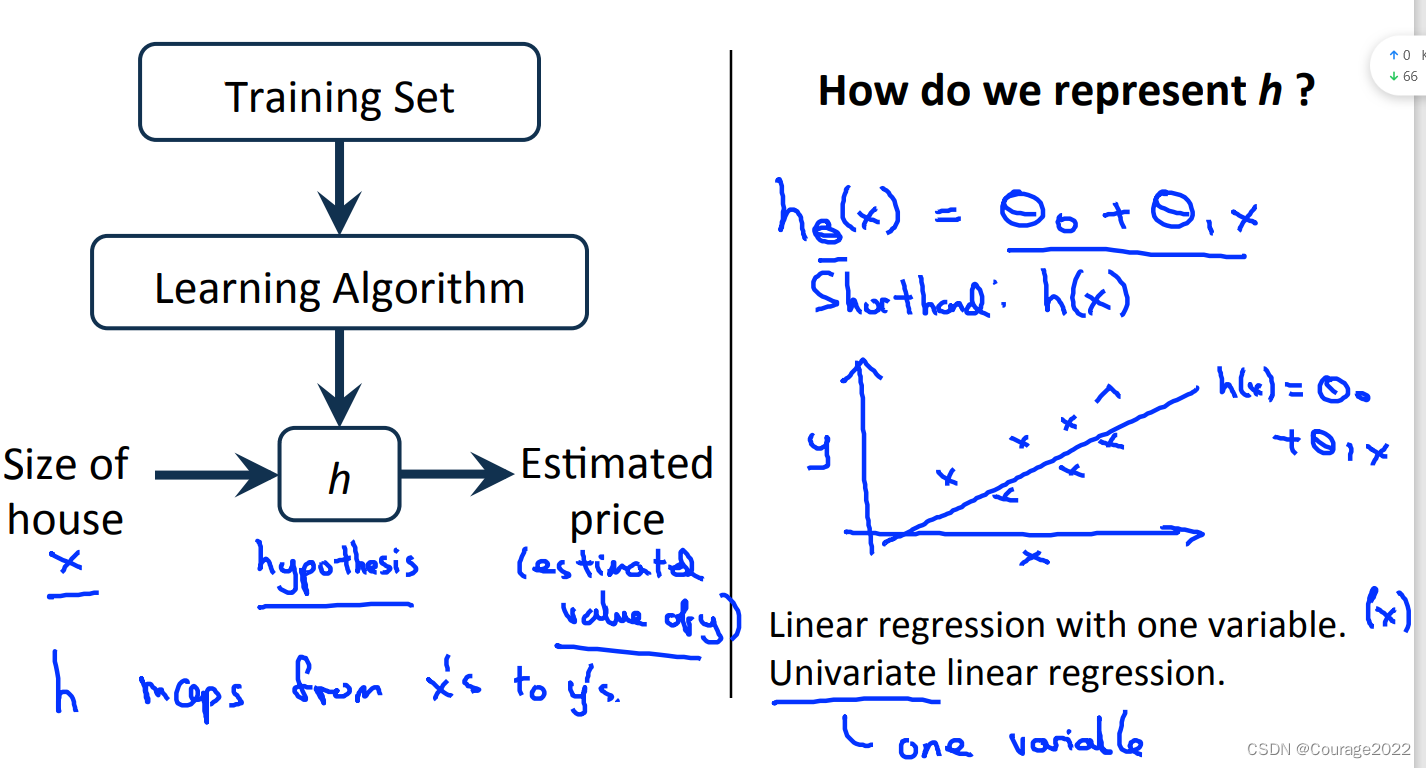
        我们给出训练集，通过学习算法得到假设函数，这样通过输入变量，经过假设函数

，得到输出变量，这样就能预测我们的放假了，那么如何评估假设函数呢？

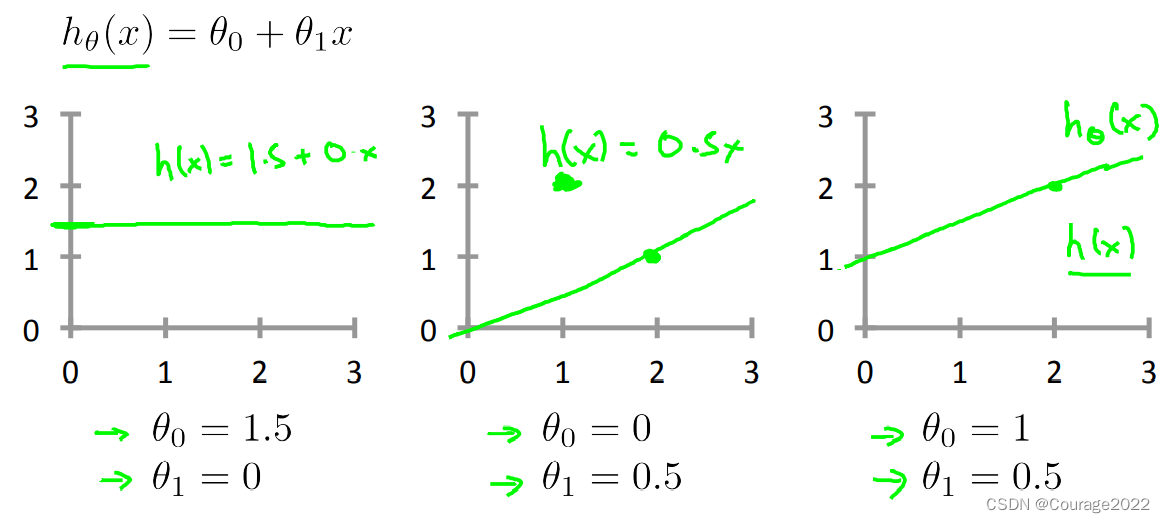
        对于一元线性回归，我们的假设函数为，这里是待预估参数，那么怎么去选择呢，上图为不同的曲线。

2.2.2 代价函数 

        我们用代价函数去描述一元线性回归模型的好坏，一元线性回归代价函数如下：

         简单来说，一共有组样本，对于每一组样本，用假设函数提供的线性回归函数拟合计算真值与假设值的平方差作为代价函数。那么不难看出，代价函数较小的假设函数有较好的拟合效果。

        那么我们先拿过原点的一元函数简单分析下：

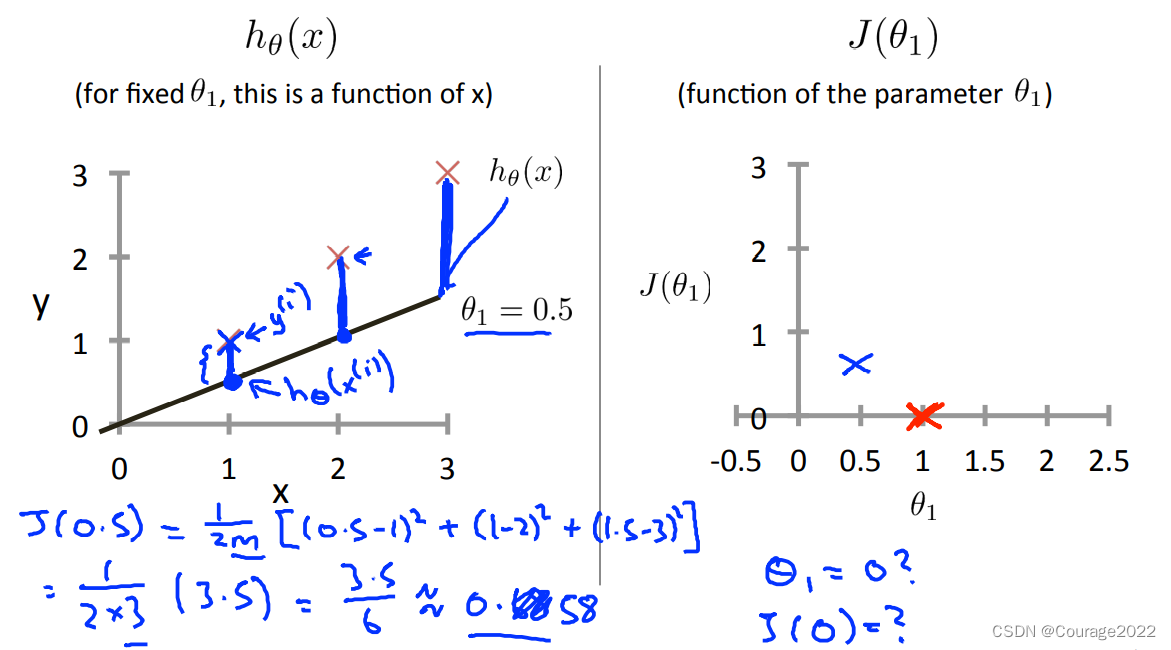
         对于每组，我们计算其代价函数值，最后我们画出关于的函数，选择最低的为最优拟合。

        那么我们现在清晰明了，对于一个一元线性回归问题，我们的假设函数为，其中待训练参数为 ，我们用代价方程来衡量拟合的好坏程度

 我们的目标是找出一对，使得代价方程最小。

         对于双参数，也是一样的，不过它的代价函数与参数的图像类似一个碗，同样不难看出，碗的底部对应了拟合最优秀的点。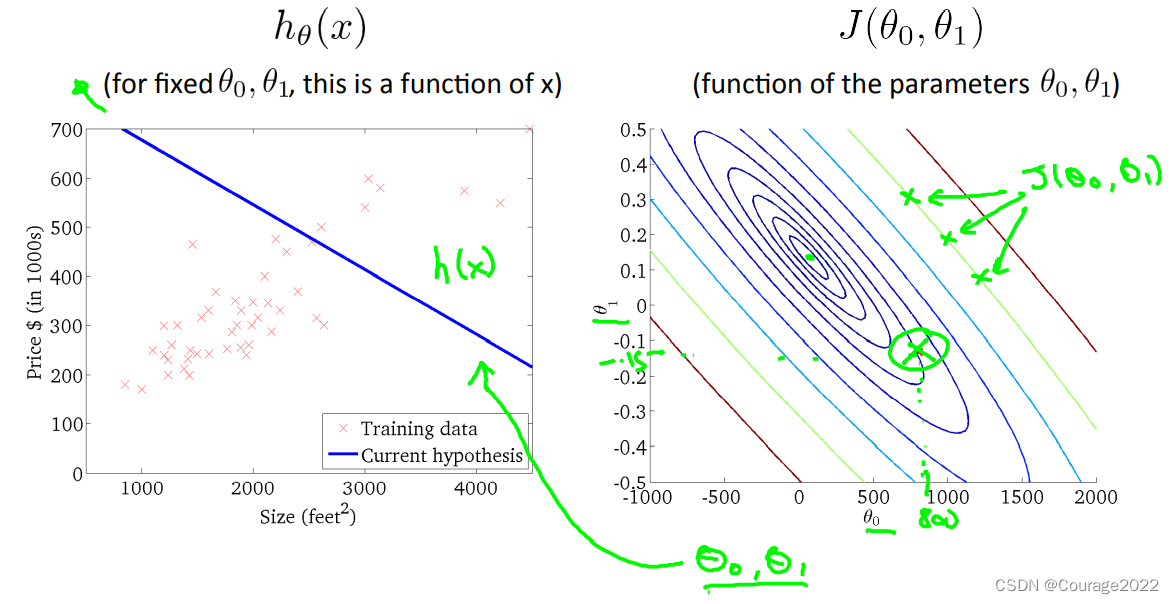 

        从等高线图上，我们可以看出：离着中间越远的点，拟合的曲线越离群同时其代价函数函数值很高。

         随着其越靠近中间的小圆，其代价函数值越小，拟合程度越好！如下图所示：

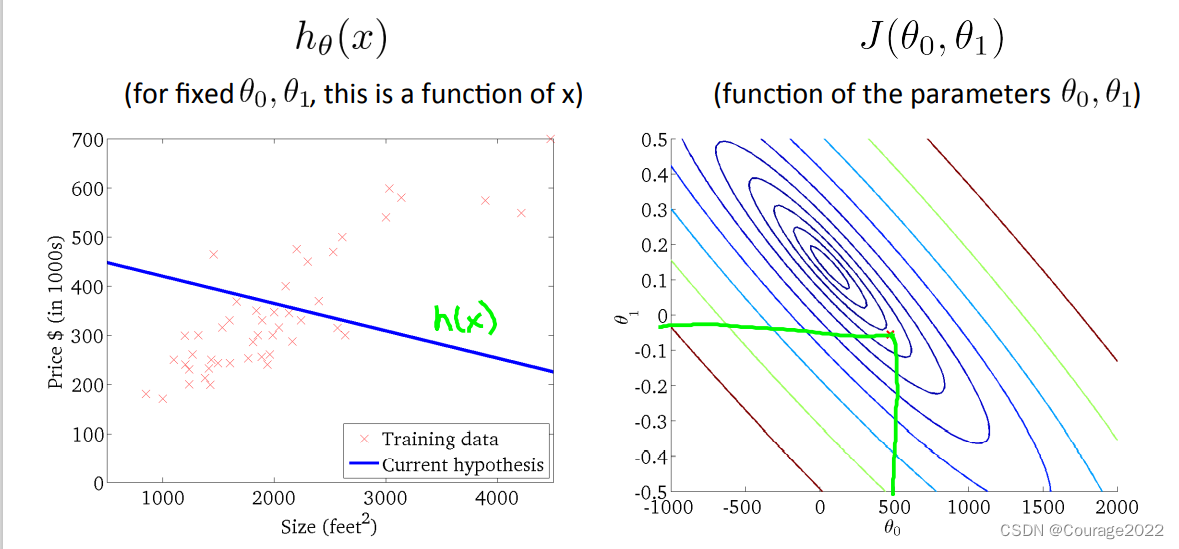
         那么如何使其越来越往中间走呢？或者说怎么找到最优的拟合参数呢？我们下面说的梯度下降法能解决这一问题。

2.3 梯度下降法 

2.3.1 引出问题

        在前面文字所讲述的部分，我们计算出了很多不同参数对应代价函数的值，我们想找一个最小的，取其假设函数作为线性回归拟合的方程。

        那么我们的问题来到：

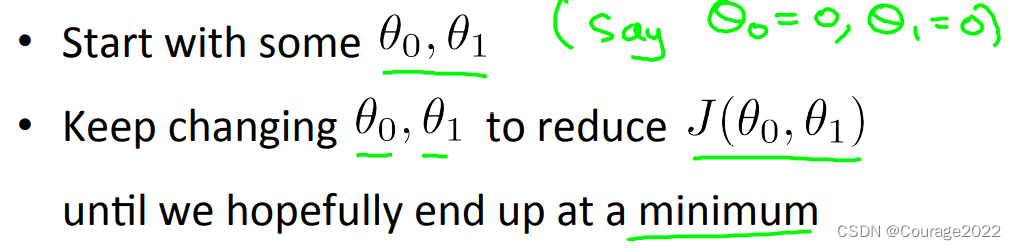
         我们根据机器画出了代价函数与参数的关系图如上图，我们想不断改变参数

 从而降低代价函数的值，最终得到一个最小值的代价函数作为拟合方程。

        那么问题来了，计算机怎么处理这个行为？①怎么控制不断降低②不同的初始点的选择可能最终有不同的结果（如上图所示）。

2.3.2 梯度下降法

        我们采用梯度下降法作为控制不断降低的方法：

        不断修改的值直至收敛：

         为什么右面的计算方法不对呢：要同时修改！

2.3.3 梯度下降法的缩放因子对梯度下降法的影响

        如何调整缩放因子以得到代价函数最小的拟合函数？或者选择缩放因子过大过小对梯度下降法有什么影响呢？

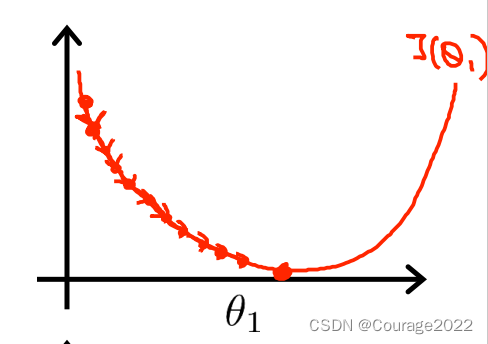
         如果代价函数的缩放因子太小，导致梯度下降的时间边长，浪费系统资源，但可以得到最终结果。

         如果代价函数的缩放因子太大，可能会导致震荡最终无法收敛。

         不过，即使不调整梯度下降的因子，其下降步长也会逐渐变小，即偏导数项在慢慢变小（曲线变平，导数下降）。因此，不用动态调整梯度下降因子最终也会收敛。

         我们把导数项展开，便得到了以下形式。