LeetCode刷题day24||回溯算法理论基础&&77. 组合--回溯

回溯算法理论基础

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。在二叉树系列中，我们已经不止一次，提到了回溯。

回溯是递归的副产品，只要有递归就会有回溯。

回溯函数也就是递归函数，指的都是一个函数。

回溯法的效率

回溯法并不是什么高效的算法——因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案

回溯法解决的问题

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等

回溯法模板

• 回溯函数模板返回值以及参数

在回溯算法中，我的习惯是函数起名字为backtracking,回溯算法中函数返回值一般为void。

回溯函数伪代码如下：

void backtracking(参数)
1

• 回溯函数终止条件

既然是树形结构，那么我们在讲解二叉树的递归 (opens new window)的时候，就知道遍历树形结构一定要有终止条件。

所以回溯也有要终止条件。

树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

所以回溯函数终止条件伪代码如下：

if (终止条件) {
    存放结果;
    return;
}
1
2
3
4

• 回溯搜索的遍历过程

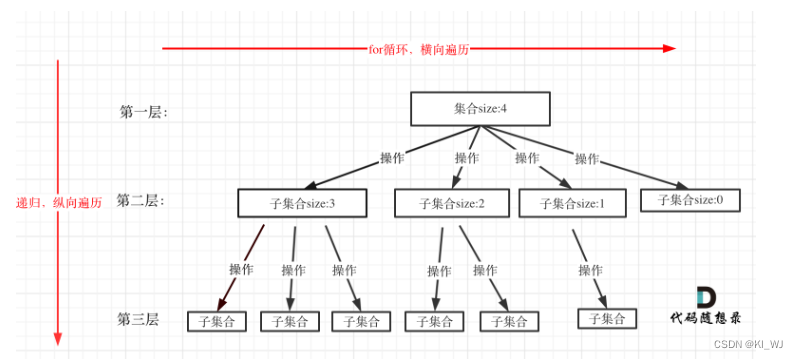
回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}
1
2
3
4
5

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

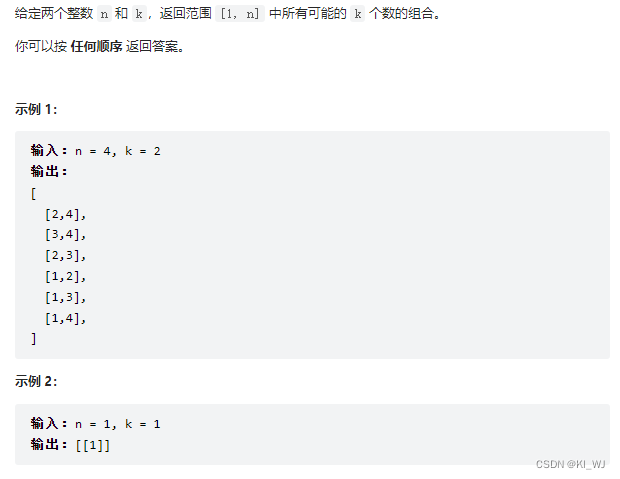
77. 组合

题目描述

题目链接

思路分析

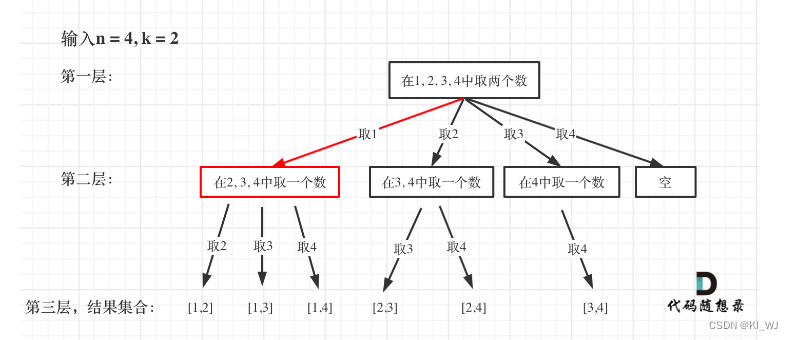
代码

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i);
            backtracking(n, k, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear();
        path.clear();
        backtracking(n, k, 1);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

剪枝操作

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {//此处剪枝
            path.push_back(i);
            backtracking(n, k, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear();
        path.clear();
        backtracking(n, k, 1);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23