• 【数据结构笔记3】- 栈和队列 基础到实战-入门到应用

    文章目录

    栈和队列

    简而言之，就是顺序表和链表在满足栈和队列出入数据的特性的基础上衍生出的新的数据结构，也就是栈和队列，他们都有两种实现方式，顺序表实现和链表实现。

    1. 栈stack

    1.1 栈的概念及结构

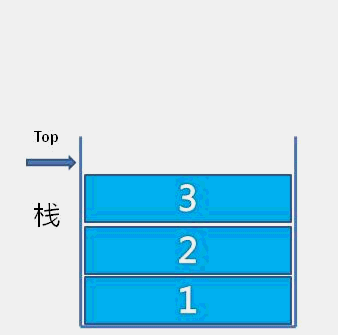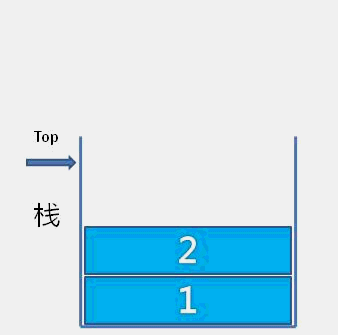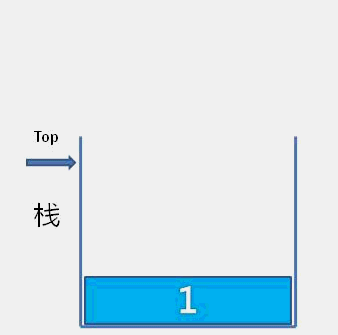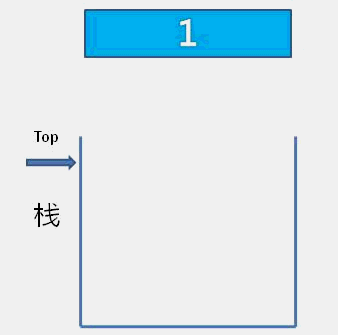
    栈是只允许在栈顶进行插入删除操作的线性结构，也看作特殊的线性表。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出***LIFO（Last In First Out）***的原则。

    • 入栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶Top。 （栈顶对应表尾）
    • 出栈：栈的删除操作叫做出栈。出数据也在栈顶Base。（栈底对应表头）

    按存储结构，栈分为顺序栈和链栈。栈的顺序存储–顺序栈。栈的链式存储–链栈

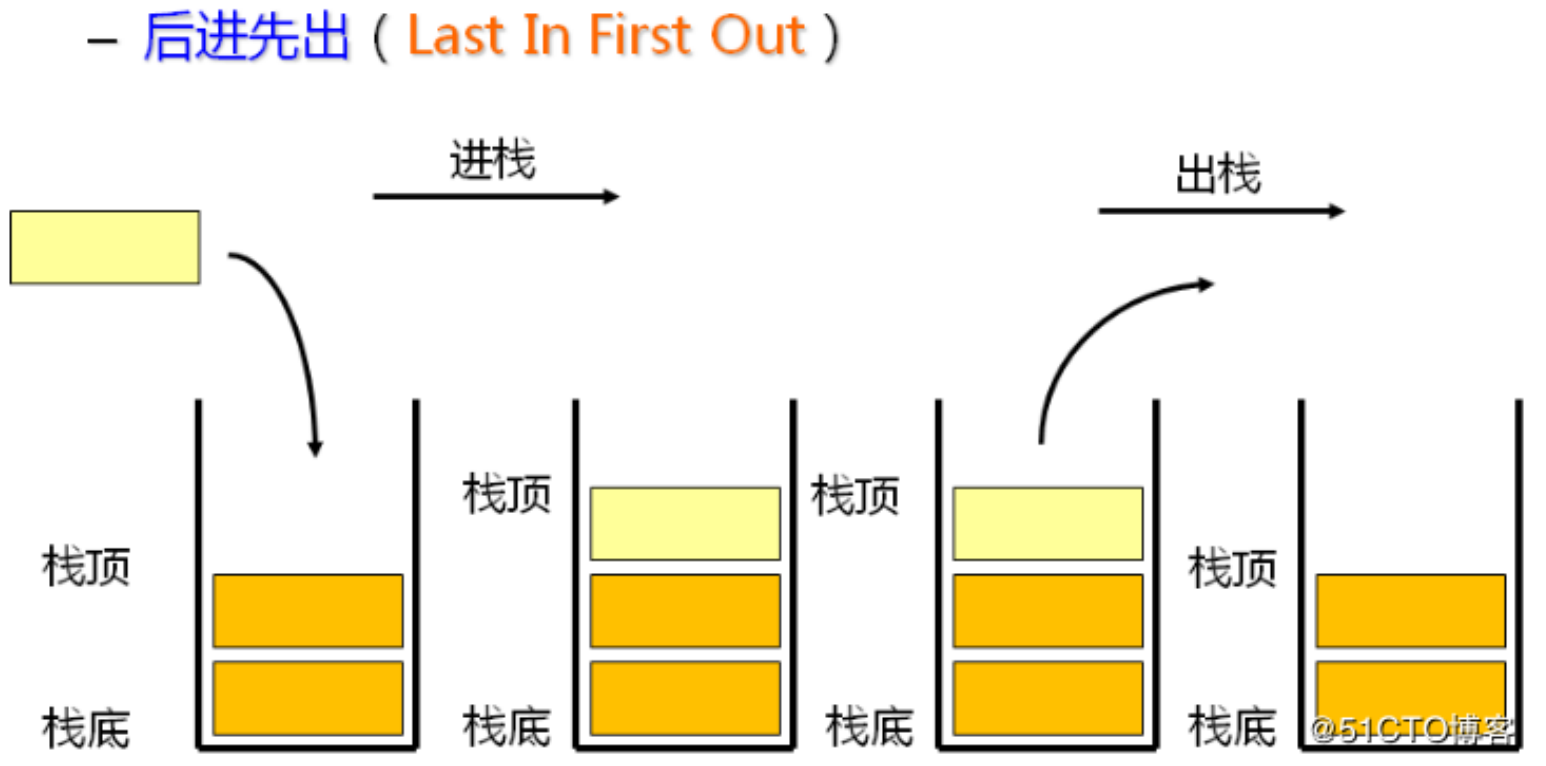
    image-20220521115328148

    栈用来解决先进后出的问题，常见的有进制转换、括号匹配问题、行编辑程序、迷宫求解、表达式求值、八皇后问题、函数递归调用。这些都在本文末尾一一讲解

    LIFO是栈的特点，栈接口函数数据插入和删除操作都是在栈顶实现：

    • 进栈nojj1bedpb
    • 出栈p1zpevqajl

    1.2 顺序栈实现

    逻辑结构如下：

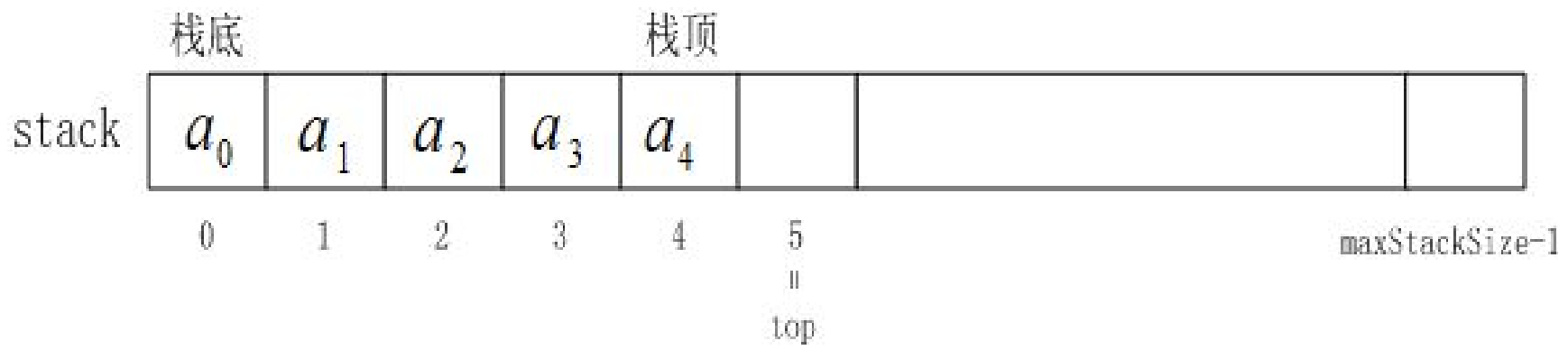
    image-20220521144056291

    顺序栈实现算法概述：利用顺序表，通过改变出入数据的方式，达到后进先出的效果。

    静态顺序表就是实现静态栈，动态顺序表实现的则是动态栈。我们一般用动态栈。

    下面是动态栈实现的代码：

    • 栈头文件
    #pragma once
#include
#include
#include
#include

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;        //栈顶，也可以用指针，但是没必要
	int capacity;   //容量
}Stack;
//初始化栈
void StackInit(Stack* ps);
//销毁栈
void StackDestory(Stack* ps);
//入栈
void StackPush(Stack* ps, STDataType x);
//出栈
void StackPop(Stack* ps);
//获取栈顶元素
STDataType StackTop(Stack* ps);
//获取栈中有效的元素个数
int StackSize(Stack* ps);
//判断栈是否为空，空则返回非零，不为空则返回0
bool StackEmpty(Stack * ps);


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 栈源文件
    #include"Stack.h"
void StackInit(Stack* ps)//初始化
{
	assert(ps);//断言判断是否为空
	//凡是传进来指针，就断言判断。凡是申请指针空间，就要判断是否成功！
	ps->a = (STDataType*)malloc(4 * sizeof(STDataType));
	if (ps->a == NULL)
	{
		printf("malloc failed\n");
		exit(-1);
	}
	ps->capacity = 4;
	ps->top = 0;
}

void StackDestory(Stack* ps)//销毁栈
{
	assert(ps);//断言判断是否为空
	free(ps->a);
	ps->a = NULL;//释放完指针要置空，否则就是野指针
	ps->top = ps->capacity = 0;
}

void StackPush(Stack* ps, STDataType x)//入栈
{
	assert(ps);//断言判断是否为空
	if (ps->top == ps->capacity)
	{
		STDataType* tmp = (STDataType*)realloc(ps->a, 2 * ps->capacity * sizeof(STDataType));
		//凡是传进来指针，就断言判断。凡是申请指针空间，就要判断是否成功！
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);//exit(0)表示正常退出，exit(x)x非零表示非正常退出
		}
		else
		{
			ps->a = tmp;
			ps->capacity *= 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(Stack* ps)//出栈
{
	assert(ps);//断言判断是否为空
	assert(ps->top);//栈空
	//ps->a[ps->top]=0;是不可取的！
	ps->top--;
}

STDataType StackTop(Stack* ps)//获取栈顶元素
{
	assert(ps);//断言判断是否为空
	assert(ps->top > 0);//栈空
	return ps->a[ps->top - 1];
}

//获取栈中有效的元素个数
int StackSize(Stack* ps)
{
	assert(ps);//断言判断是否为空
	return ps->top; //0~(ps->top-1)
}

bool StackEmpty(Stack* ps) //判断栈是否为空，空则返回1，不为空则返回0
{
	assert(ps);
	return ps->top == 0;//代码简洁
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 主函数测试
    #include"Stack.h"
void Stacktest()
{
	Stack st;
	StackInit(&st);
	StackPush(&st, 1);
	StackPush(&st, 2);
	StackPush(&st, 3);
	StackPush(&st, 4);
	StackPush(&st, 5);
	while (!StackEmpty(&st))
	{
		printf("%d\n", StackTop(&st));
		StackPop(&st);
	}   //符合栈的性质，相对而言的后进先出（相对于栈里的数据）
	StackDestory(&st);
}
int main()
{
	Stacktest();
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21

    入栈顺序：12345，出栈顺序：54321

    image-20220521145034808

    1.3 链栈实现

    逻辑结构如下：

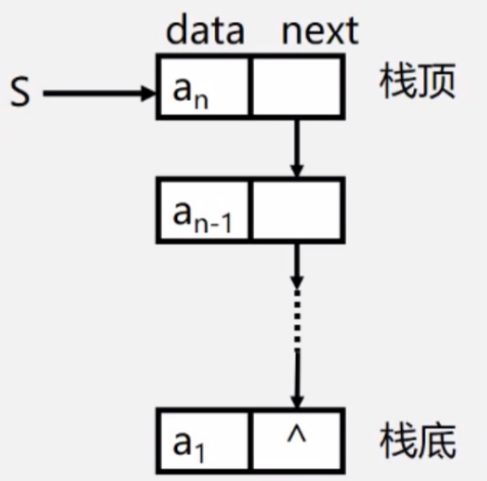
    image-20221015145229828

    用一个头指针指向栈顶的链表，对应只提供头插和头删两个方法实现。模拟实现栈的先进后出。很简单就不在此赘述。

    1.4 栈和递归

    • 若一个对象部分地包含自己，或用自己给自己定义，则称这个对象是递归的。

    • 若一个过程直接的或间接的调用自己，则称这个过程是递归过程。如函数的递归调用、数的遍历、斐波那契数列等

    • 著名的迷宫求解问题和Hanoi塔问题都能用递归求解

      image-20221016173259514 image-20221016173309715

    • 递归问题-用分治法求解

      分治法，对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解。

      分治求解递归问题算法的一般形式

      image-20221019152931667
    1.4.1 函数调用过程

    通常,一个函数在运行期间调用另一个函数时,在运行被调用函数之前,系统需先完成3件事:

    1. 将所有的实参、返回地址等信息传递给被调用函数保存;
    2. 为被调用函数的局部变量分配存储区;
    3. 将控制转移到被调函数的入口。

    而从被调用函数返回调用函数之前,系统也应完成3件事

    1. 保存被调用函数的计算结果;
    2. 释放被调用函数的数据区;
    3. 依照被调用函数保存的返回地址将控制转移到调用函数。

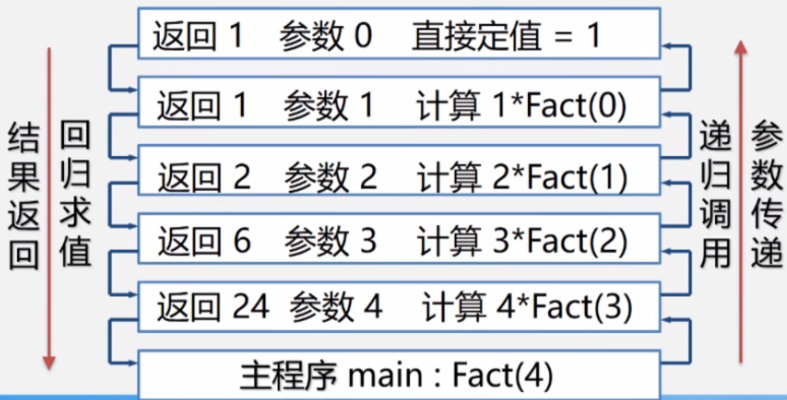
    为了保证递归正确执行，系统会建立一个递归工作栈，记录整个递归函数运行期间使用的数据存储区。每一层递归所需信息构成工作记录，包括实参，所有的局部变量，以及上一层的返回地址，每进入一层递归就产生一个新的工作记录压入栈顶，每退出一层递归，就从栈顶弹出一个工作记录，则当前执行层的工作记录必是递归工作栈栈顶的工作记录，称这个记录为活动记录。

    递归阶乘n!的过程

    int Fact(int x)
{
	if(x==0)return 1;
	else return x*Fact(x-1);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    image-20221019155658530

    1.5 括号匹配问题

    20. 有效的括号 - 力扣（Leetcode）这是相应的括号匹配问题力扣题

    括号匹配就是“( )”“{ }”“[ ]”这些括号满足一一对应关系。可以嵌套定义，如：({()})。而

    括号匹配问题就是：

    给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。有效字符串需满足：

    1. 左括号必须用相同类型的右括号闭合。
    2. 左括号必须以正确的顺序闭合。
    3. 每个右括号都有一个对应的相同类型的左括号

    设计思路：

    • 如果碰到的是左圆括号或者左大括号，直接压栈；
    • 如果碰到的是右圆括号或者右大括号，就直接和栈顶元素配对：如果匹配，栈顶元素弹栈；反之，括号不匹配；

    这里使用C++来实现算法

    class Solution {
public:
	bool isValid(string s) {
		stack<char>storage;
		for (int i = 0; i < s.size(); i++)
		{
			if (s[i] == '(' || s[i] == '[' || s[i] == '{')
				storage.push(s[i]);
			else
			{
				if (s[i] == ')')
				{
					if (!storage.empty() && storage.top() == '(')storage.pop();
					else return false;
				}
				else if (s[i] == '}')
				{
					if (!storage.empty() && storage.top() == '{')storage.pop();
					else return false;
				}
				else if (s[i] == ']')
				{
					if (!storage.empty() && storage.top() == '[')storage.pop();
					else return false;
				}
			}
		}
		return storage.empty();
	}
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30

    1.6 表达式求值问题

    所谓表达式，就是由变量、常量以及运算符组合而成的式子。其中，常用的运算符无非 !（阶乘运算符）、^（指数 运算符）、+、-、*、/ 、( ) 这几种，比如 3!+4*2/(1-5)^2 就是一个表达式。 那么，如何用栈结构求一个表达式的值呢。用后缀表达式法。

    什么是后缀表达式？就是将表达式中所有运算符放在它的运算项后面

    这里以 3!+4*2/(1-5)^2 为例：6+8/16

    • ! 运算符对应的运算项为 3，转换后得到3!
    • +运算符对应的运算项是 3! 和 4*2/(1-5)^2，转换之后得到：3! 4*2/(1-5)^2 +
    • *运算符对应的运算项是 4 和 2，转换之后得到 4 2 *
    • / 运算符对应的运算项是4 2 *和(1-5)^2，转换后得到 4 2 * (1-5)^2 /
    • -运算符对应的运算项是 1 和 5，转换后得到1 5 -
    • ^运算符对应的运算项是1 5 -和2，转换后得到 1 5 - 2 ^。

    整合之后，整个普通表达式就转换成了 3 ! 4 2 * 1 5 - 2 ^ / +这就是其对应的后缀表达式。

    得到的后缀表达式，如何计算？首先创建一个栈。接着按照从左到右的顺序扫描后缀表达式，遇到运算项就入栈。遇到n元运算符，就出栈顶元素n个计算并将计算结果压回栈中。代码实现应注意的是：从栈出来的先后顺序，对应原来运算的哪一个运算项！

    如：遇到阶乘（一元运算符），出栈顶计算。遇到乘法（二元运算符），出栈顶两元素计算并压回栈中。循环上述操作，最后栈中最后一个元素，即为此运算项即为整个表达式的值。

    • 根据后缀表达式求值代码实现
    double calculate(char* out)
{
	int index = 0;
	stack<double>result;
	while (out[index] != '\0')
	{
		char c = out[index];
		switch (c)
		{
			case '!':
			{
				double i = result.top();
				result.pop();
				double end = 1;
				while (i != 1) end *= i-- ;
				result.push(end);
				break;
			}
			case '*':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left * right);
				break;
			}
			case '/':
			{
				double right = result.top();//被除数
				result.pop();
				double left = result.top();//除数
				result.pop();
				if (!right)
				{
					cout << "分母为零，错误" << endl;
					exit(-1);
				}
				else
				{
					result.push(left / right);
					break;
				}
			}
			case '+':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left + right);
				break;
			}
			case '-':
			{
				double right = result.top();//被减数
				result.pop();
				double left = result.top();//减数
				result.pop();
				result.push(left - right);
				break;
			}
			case '^':
			{
				double exp = result.top();//指数
				result.pop();
				double base = result.top();//底数
				result.pop();
				if (!base)
				{
					cout << "底数为零" << endl;
					exit(-1);
				}
				else
				{
					double end = 1;
					for (int i = 0; i < exp; i++)
					{
						end *= base;
					}
					result.push(end);
					break;
				}
			}
			default:
			{
				result.push(c - 48);
			}
		}
		index++;
	}
	return result.top();

}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    1.6.1 根据表达式求后缀表达式

    上面讲过了如何求解表达式：表达式–后缀表达式–利用栈运算，那么如何获得后缀表达式？

    首先看规则：

    普通表达式转换为后缀表达式需要用到一个空栈（假设名为Optr）和一个空数组（数组名）

    • 如果为 ‘0’~‘9’ 的字符，将其添加到 postexp 数组的末尾；
    • 如果该字符为除 ‘(’ 和 ‘)’ 以外的运算符，将其与 Optr 栈顶的运算符进行优先级比较（如乘法高于加法），如果该运算符优先级高于或等于栈顶运算符，则将其入栈；反之，如果该运算符优先级小于栈顶运算符，则将栈顶运算符出栈并添加到 postexp 数组的尾部，然后继续拿当前运算符同新的栈顶运算符做大小比较，以此类推。
    • 如果该字符为 ‘(’ 运算符，直接入栈；如果为 ‘)’ 运算符，依次取 Optr 栈顶运算符并将其添加到 postexp 数组末尾，直到遇到 ‘(’ 字符为止（注意，‘(’ 字符也从栈顶取出，但不将其添加 postexp 数组中）。

    依照以上处理过程，直到将普通表达式遍历完毕，如果 Optr 栈中仍有运算符，依次将它们出栈并添加到 postex数组尾部。最终，postexp 数组内存储的表达式就是转换后的后缀表达式。

    总结一句：运算项直接放数组中，运算符压入栈中，只有遇到比栈顶运算符优先级低的或栈空才出栈放入数组中。括号单独考虑。

    如此一来运算符优先级高的就紧随运算项，先运算。运算符优先级低的往往在后缀表达式最右边。

    下面是表达式3 ! 4 2 * 1 5 - 2 ^ / +转换为后缀表达式的过程：（按序号看）

    image-20221029002310515

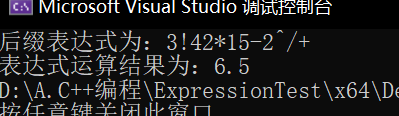
    代码实现

    void transform(char* expr, char* out)
{
	stack<char>temp;
	int index = 0;//作为输出数组的下标
	int i = 0;//表达式的下标
	while(expr[i]!='\0')
	{
		char c = expr[i];
		switch (c)
		{
			case '!':
			{
				while (!temp.empty()) 
				{
					if (temp.top() == '!')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('!');
				i++;
				break;
			}case '*':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('*');
				i++;
				break;
			}case '/':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('/');
				i++;
				break;
			}case '+':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' 
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('+');
				i++;
				break;
			}case '-':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*'
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('-');
				i++;
				break;
			}case '(':
			{
				temp.push('(');
				i++;
				break;
			}case ')':
			{
				while (temp.top() != '(')
				{
					char ch = temp.top();
					temp.pop();
					out[index++] = ch;
				}
				temp.pop();//此时栈顶为（
				i++;
				break;
			}case '^':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!'||temp.top()=='^')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('^');
				i++;
				break;
			}default :
			{
				out[index++] = c;
				i++;
				break;
			}
		
		}
	}
	//此时将栈中多有的数据逐一出栈
	while (!temp.empty())
	{
		out[index++] = temp.top();
		temp.pop();
	}
	out[index] = '\0';//最后给后缀表达式加上尾\0
}
int main() {
	char* s = (char*)malloc(15 * sizeof(char));
	char* out = (char*)malloc(13 * sizeof(char));
	char temp[] = "3!+4*2/(1-5)^2";
	//cout << strlen(s);
	for (int i = 0; i < 15; i++)
	{
		s[i] = temp[i];
	}
	transform(s,out);
	cout << "后缀表达式为："<< out << endl;
	cout <<"表达式运算结果为："<< calculate(out);

}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    image-20221029141426025

    1.7 Hanoi塔问题

    2. 队列

    2.1 队列的概念及结构

    队列：只允许一端插入数据，另一端删除数据作的线性结构。队列中数据遵守先进先出FIFO（First In First Out）原则。

    • 入队：进行插入操作的一端称为队尾
    • 出队：进行删除操作的一端称为队头

    按存储结构，队列分为顺序队和链队。队列的顺序存储–顺序队，队列的链式存储–链队。

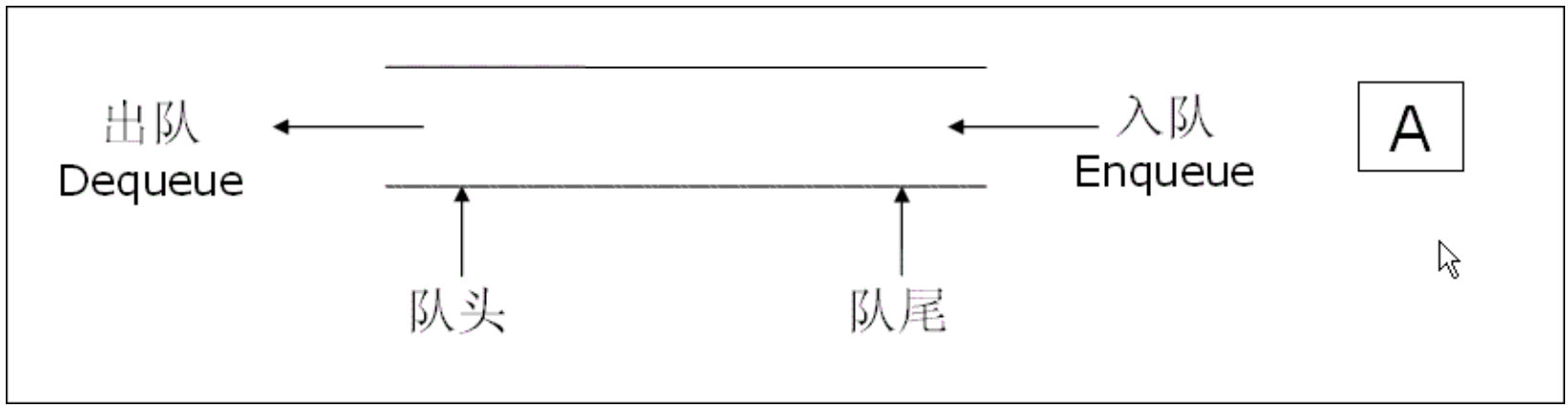
    image-20220521145450941

    队列用于解决先进先出的问题，如脱机打印输出、多用户系统中多个用户排成队，分时地循环使用CPU和主存、网络电文传输，按到达时间先后顺序依次进行。

    2.2 链队的实现

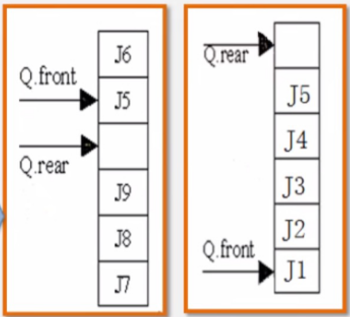
    顺序队相比于链队，顺序队每次出数据都需要向前移动整个队列数据，相对浪费时间。相比之下链队更加优秀。用两个指针分别指向队列的队头和队尾（初始状态如图a）入队出队的过程其实就是无头单向链表的实现（头插和尾删），具体请看：（99条消息) C/C++【数据结构笔记】(顺序表&链表)_Answer-2296的博客-CSDN博客）

    image-20220906171210437

    • 入队

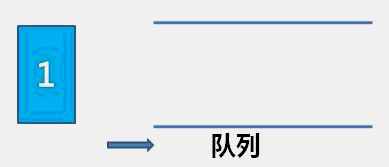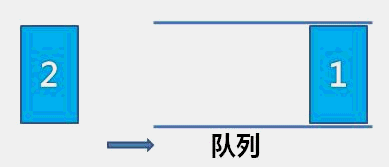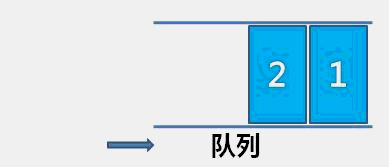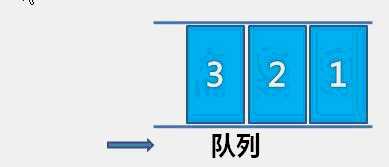
      c1aar9uajz

    • 出队

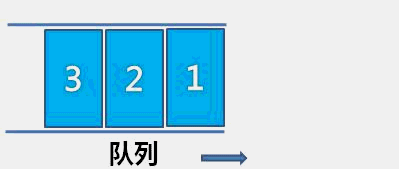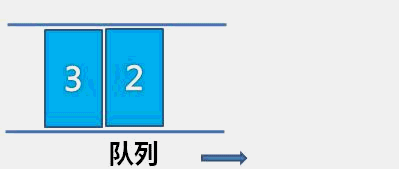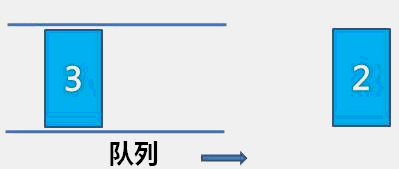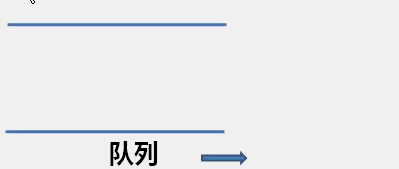
      wasdo17tpz

    • 队列头文件

    #pragma once
#include
#include
#include
#include

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;//无头单向链表的结点

typedef struct Queue
{
	//用这个结构体来代表队列
	QueueNode* head;//指向队列的头
	QueueNode* tail;//指向队列的尾
}Queue;
//队列初始化
void QueueInit(Queue* qp);
//销毁队列
void QueueDestory(Queue* qp);
//入队(队尾入队)
void QueuePush(Queue* qp, QDataType x);
//出队(队头出队)
void QueuePop(Queue* qp);
// 获取队列头部元素
QDataType QueueFront(Queue* qp);
// 获取队列队尾元素
QDataType QueueBack(Queue* qp);
// 获取队列中有效元素个数
int QueueSize(Queue* qp);
// 检测队列是否为空，如果为空返回1，如果非空返回0
bool QueueEmpty(Queue* qp);

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 队列源文件
    #pragma once
#include"Queue.h"

void QueueInit(Queue* qp)//队列初始化
{
	assert(qp);
	qp->head = qp->tail = NULL;//初始化都置成空！
}

void QueueDestory(Queue* qp)//销毁队列
{
	assert(qp);
	QueueNode* cur = qp->head;
	while (cur)//最后一个结点的next值位空
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}//逐个销毁
	qp->head = qp->tail = NULL;//没用的指针都置成空，避免野指针
}

void QueuePush(Queue* qp, QDataType x)//入队(队尾入队)
{
	assert(qp);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (!newnode)
	{
		printf("malloc failed\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;//构建好数据结点
	if (qp->tail == NULL)
	{
		qp->head = qp->tail = newnode;
		//如果是空队列，队尾队头都要变
	}
	else
	{
		qp->tail->next = newnode;
		qp->tail = newnode;//重新改变队尾
	}
}

void QueuePop(Queue* qp)//出队(队头出队)
{
	assert(qp);
	assert(qp->head);//队列非空才能出队
	if (qp->head->next == NULL)
	{
		free(qp->head);
		qp->head = qp->tail = NULL;
	}//队列只有一个结点，则置空队列（qp->tail=NULL）如果没单独考虑，qp->tail会成为野指针。
	else
	{
		QueueNode* next = qp->head->next;
		free(qp->head);
		qp->head = next;
	}
}

QDataType QueueFront(Queue* qp)// 获取队列头部元素
{
	assert(qp);
	assert(qp->head);
	return qp->head->data;
}

QDataType QueueBack(Queue* qp)// 获取队列队尾元素
{
	assert(qp);
	assert(qp->head);
	return qp->tail->data;
}

int QueueSize(Queue* qp)// 获取队列中有效元素个数
{
	assert(qp);
	int size = 0;
	QueueNode* cur = qp->head;
	while (cur)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

bool QueueEmpty(Queue* qp)// 检测队列是否为空，如果为空返回1，如果非空返回0
{
	assert(qp);
	return qp->head == NULL;//简洁！
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 主函数实现
    #include"Queue.h"
void Queuetest()
{
	Queue  q;
	QueueInit(&q);
	QueuePush(&q, 1);
	QueuePush(&q, 2);
	QueuePush(&q, 3);
	QueuePush(&q, 4);
	QueuePush(&q, 5);
	while (!QueueEmpty(&q))
	{
		printf("%d\n",QueueFront(&q));
		QueuePop(&q);//输出完删除，模拟栈出过程
	}
}
int main()
{
	Queuetest();
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20

    队列入队顺序12345，出队顺序12345

    image-20220521153525446

    2.3 顺序队实现

    用顺序表头删和尾插分别模拟顺序队的出队和入队，相比于链队，顺序队每次出队都需要将顺序队中所有的元素前移，浪费时间。

    而队列的顺序存储也有静态顺序存储和动态顺序存储之分

    2.4 环形队列

    实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列可以使用数组，实现，也可以使用链表实现。

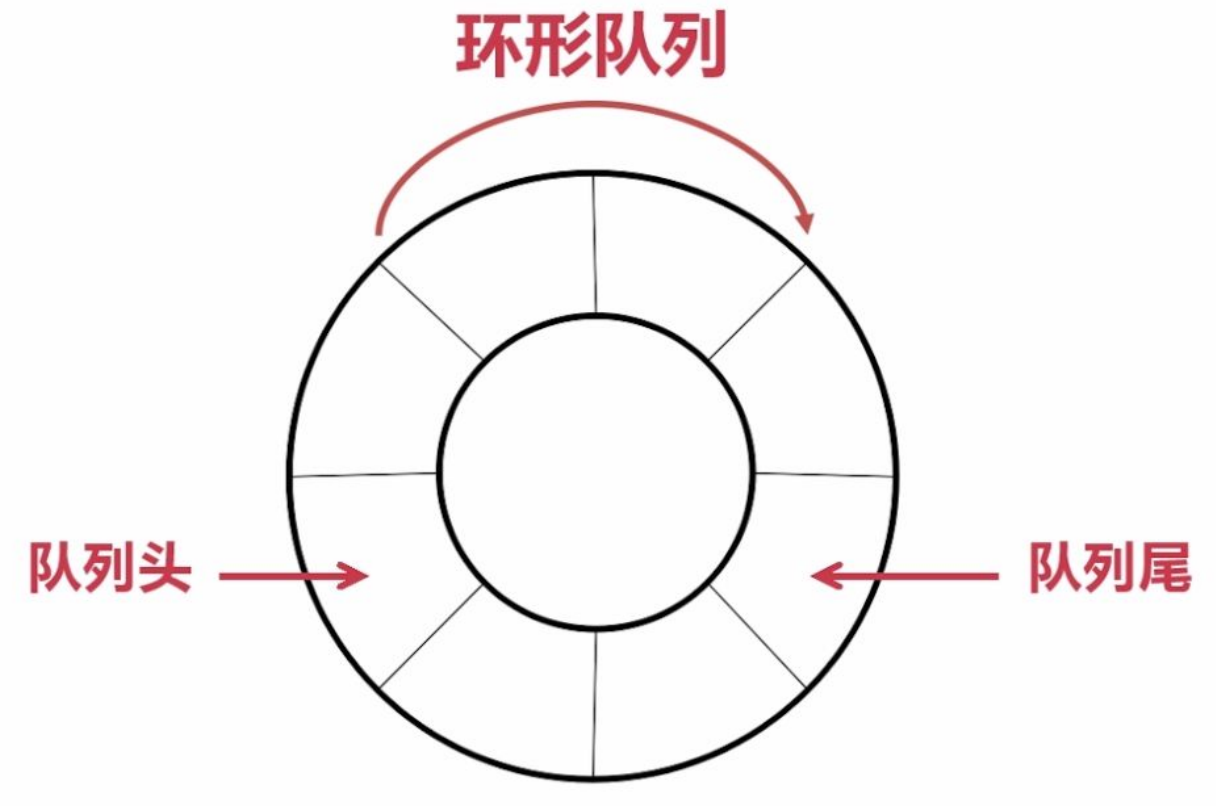
    image-20220521153943748 image-20220521154807784
    • 内存上并没有环形的结构，因此环形队列实际上是数组的线性空间来实现的。
    • 当数据到了尾部该如何处理呢？它将转回到原来位置进行处理，通过取模操作来实现

    这里用数组实现的环形队列为例。

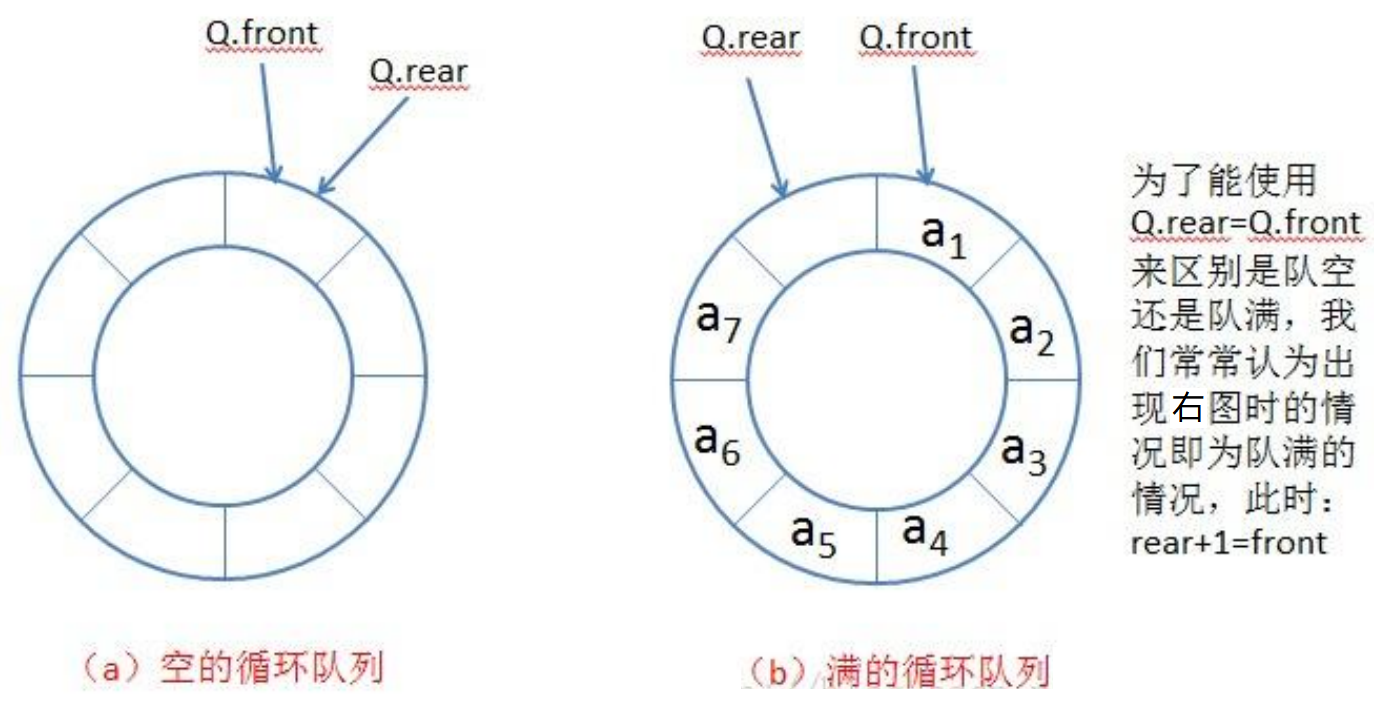
    Q.front表示队头，初始值为0。

    Q.rear表示队列最后一个元素的后一个位置（预留一个空间，作为约定，方便判断队列是否为空）。

    maxSize: 数组的最大容量

    我们用求模运算来实现循环。一般来说队头位置固定为0，每次出队需要将队列中所有的元素前移，十分浪费空间。对此我们不固定队头，出队，只需要前移队头！

    //插入元素
Q.base[Q.rear]=x;
Q.rear=(Q.rear+1)%maxSize;
//删除元素(出队)
x=Q.base[s.front];//是否删除前返回数据因人而异
Q.front=(Q.front+1)%maxSize;

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6

    • 队列的两种状态

      • 队空：front == rear

      • 队满：(rear+1)%maxSize == front//队头前始终空一个位置

        image-20221019185012606

    • 环形队列实现代码

    #include
using namespace std;
#define MAXSIZE 11
typedef int QueueDataType;
struct Queue{
	QueueDataType* base;
	int front;
	int rear;
};

//初始化环形队列
void QueueInit(Queue& Q)
{
	Q.base = new QueueDataType[MAXSIZE];
	//C语言写法：Q.base=(QueueDataType*)malloc(sizeof(QueueDataType)*MAXSIZE);
	if (!Q.base)exit(-1);
	Q.front = Q.rear = 0;
}

//入队
void QueuePush(Queue& Q, QueueDataType data)
{
	if ((Q.rear + 1) % MAXSIZE == Q.front)
	{
		cout << "入队失败，队列已满" << endl;
		exit(-1);
	}
	Q.base[Q.rear] = data;
	Q.rear = (Q.rear + 1) % MAXSIZE;
}
//出队
void QueuePop(Queue& Q)
{
	if (Q.rear == Q.front)
	{
		cout << "对空，出队失败" << endl;
		exit(-1);
	}
	Q.front = (Q.front + 1) % MAXSIZE;
}
//取队头元素
QueueDataType QueueTop(Queue Q)
{
	if (Q.rear == Q.front)
	{
		cout << "队空，取队头失败" << endl;
		exit(-1);
	}
	else
	{
		return Q.base[Q.front];
	}
}
int main()
{
	Queue q;
	QueueInit(q);
	for (int i = 0; i < 10; i++)
	{
		QueuePush(q, i);
	}
	for (int i = 0; i < 10; i++)
	{
		int temp = QueueTop(q);
		QueuePop(q);
		cout << temp<<" ";
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    image-20221020003824654

    3. 栈和队列区别与联系

    栈中的数据元素遵守后进先出***LIFO（Last In First Out）***的原则。并且是相对而言，多为后进先出是指，栈现有的数据是后进先出，所以可以出现先进栈的数据比后进栈的数据先出（比如数据进栈立马出栈，这时它就比后面数据先出来，所以说栈的后进先出是相对而言的）

    队列中数据遵守先进先出FIFO（First In First Out）原则。并且是绝对而言，只要是先进队列的一定是先出来的。

    • 静态顺序表实现静态栈，动态顺序表实现动态栈。而顺序表的实现方式是数组，通过数组是否定长即可相应类型的栈。而数据结构的实现方式和顺序表如出一辙，具体不同体现在栈的先进后出的特点，所以相应的函数有所不同。
    • 队列的实现则和链表的实现即为相似，都定义了结点这个结构体作为单元，有些不同的是队列还定义了Queue结构体包装有两个指针，分别指向队列头和队列尾。而链表直接用第一个结点（或第一个结点的地址）作为链表的标识。此外具体实现上队列遵循先进先出，所以函数实现上也有所不同。

    3.1 栈编码总结

    分清数据在哪里发生变化！Stack中的指针，top，capacity在哪里变化，怎么变？对于指针申请空间，我们用函数包装好，内部做判断，capacity和和空间绑定在一块，所以capacity也是在函数内部来变化！top作为待插入数据的位置坐标，是在入栈出栈的时候做出改变。

    3.2 队列编码总结

    在出队函数实现时尤为需注意野指针的诞生，因为一般队列足够长时，出队只需要操作对头，并释放对应数据。但如果队列只有一个数据，这时释放完空间，却没有对队尾指针修改，此时尾指针指向的是一个未知空间！

    4.栈和队列的相互转换

    (224条消息) 【数据结构拓展笔记】_栈和队列的相互转换_Answer-2296的博客-CSDN博客

    由于篇幅过长，转战。

  • 相关阅读:
    看看CabloyJS是如何异步加载并执行go wasm模块的
    Google Earth Engine（GEE）——用geometry点来改变选的影像范围，并进行加载的APP
    从零用VitePress搭建博客教程(5) - 如何自定义页面模板、给页面添加独有的className和使页面标题变成侧边目录？
    腾讯二面：@Bean 与 @Component 用在同一个类上，会怎么样？
    共享单车之租赁需求预估
    LlamaIndex：将个人数据添加到LLM
    QEM网格简化算法学习
    MAUI Blazor 权限经验分享 (定位,使用相机)
    phpqrcode生成二维码
    android MediaStore.ACTION_IMAGE_CAPTURE 调用照相机返回图片太小问题解决方法
  • 原文地址：https://blog.csdn.net/weixin_63267854/article/details/127593574