链式二叉树（1）

链式二叉树是什么 

链式二叉树的基本操作（遍历 搜索）

链式二叉树的价值（基础 oj）

重点：递归 栈帧 分治

遍历：前序中序后序遍历层序遍历

搜索：

这棵树有多少个结点

某一层有多少个结点

叶子结点的个数

某个地方值为特定值的结点如何搜索

oj;

单值二叉树

二叉树深度

一 链式二叉树是什么

之前我们学习了单链表，链式二叉树其实类似于一条一条单链表链接而成的一棵树型结构，根在上，叶在下。符合树的基本特征，并且父子节点之间通过以链表的方式链接

 大概是这样的一个样子。

二 链式二叉树的价值

  链式二叉树和线性表不太一样，她的增删查改没有太大的意义。因为增删会破坏原来树的结构，查改的话不如用线性表。因此链式二叉树的基本操作是搜索和遍历。学习链式二叉树这种其他类型的树的子结构其实在为学习后续的搜索二叉树，AVL树，红黑树，B树系列打基础，并且链式二叉树的题目在oj中出现的频率比较高，因此学习链式二叉树，起到了一个承上启下的作用

 因此知道了为什么学习链式二叉树，接下来我们就由此出发学习链式二叉树的相关操作

三 链式二叉树的遍历

由于链式二叉树的遍历比较复杂，因此我们学习的时候由浅入深的进行学习。先给出一棵链式二叉树，然后先初步体会前中后序遍历的效果，之后我们再根据思路，写出对应的代码，为了加深理解，画出对应的递归展开图。

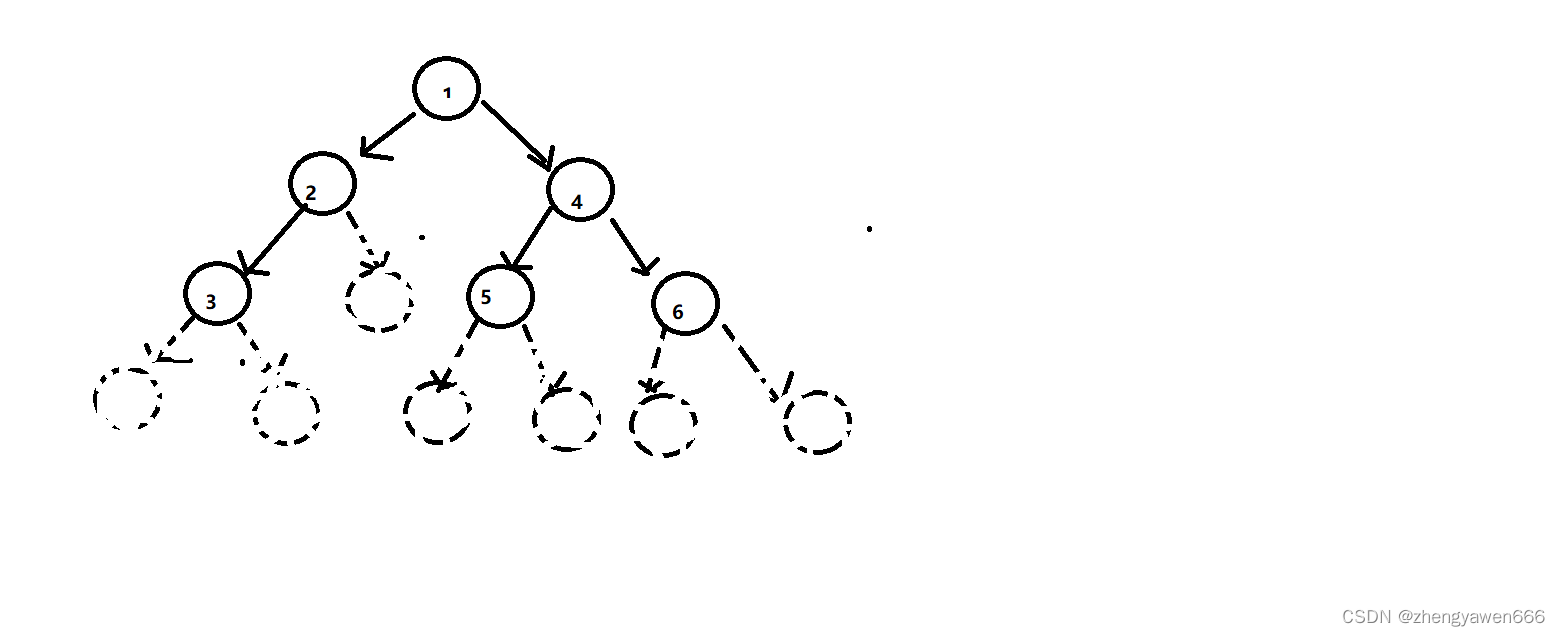
以这样的一棵树为例子

#include<assert.h>
#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
 
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	assert(node);
 
	node->data = x;
	node->left = NULL;
	node->right = NULL;
 
	return node;
}
 
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
 
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
 
	
	return node1;
}

 其实前中后序遍历就是访问结点的时机不同

1 前序遍历

思路：先去访问根节点，之后访问左子树，再访问右子树。访问左右子树的时候也是如此，比如访问左子树的时候也需要先去访问该左子树的根节点，再去访问左子树的左子树，再访问左子树的右子树。这样子递归下去，直到左子树之后没有数据了（空节点），那么代表这一层的左子树访问完毕，返回给上一层，那么该层接下来就要去访问右子树，右子树访问完毕之后再返回给该层的上层，直到递归出去。

先以这样的一棵树为例子，如果采取前序遍历的方法的话，那么依次访问到的元素是：

（将空节点以#替代）

1 2 3 # # # 4 5 # # 6 # #

代码：

void PerOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	printf("%d ", root->data);
	PerOrder(root->left);
	PerOrder(root->right);
 
}
int main()
{
	BTNode*ret=CreatBinaryTree();
	PerOrder(ret);
	return 0;
}

由于创建结点的时候是创建该结点的同时将该结点的左右结点设置为NULL，因此递归判断返回条件的时候应该是root==NULL而非rooa->data==NULL

递归展开图：

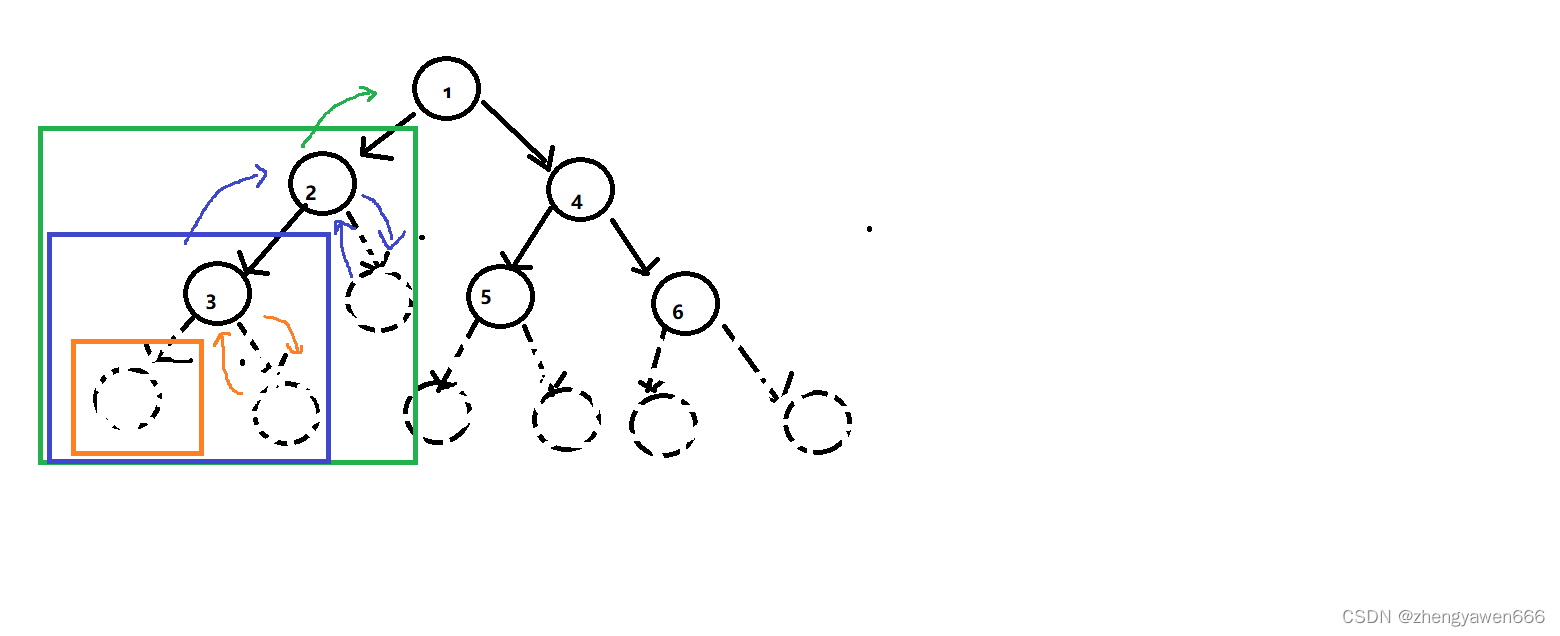
因为访问左子树和右子树的思路是差不多的，因此只画左边

不同颜色的方框和线条代表不同的层次

1先打印了1 之后将整棵树分为绿色方框圈起来的左右子树，紧接着去访问最外层的这棵树的左子树

 2 将这棵左子树看做是一棵独立的树，之后先去访问这棵树的根节点，再去访问这棵树的左子树，以蓝色方框圈出来的是这一层次的左子树

3 之后可以看做3为根结点的一棵独立的树，去访问这棵树的左子树，由于这一棵树的左子树为空，所以返回了

注意，注意，注意：返回不是返回给最外层，是返回给该层的上一层。层层返回的。比如橙色返回是返回给蓝色的，代表这一棵树的左子树已经访问完成了，该去访问蓝色这一层次的右子树了。并且访问右子树的时候也是遵循根结点，左子树，右子树的访问顺序的。但是由于3的右子树为NULL，因此也返回了，此时3这棵蓝色方框圈起来的树作为2这个绿色方框圈起来的左子树已经访问完毕了，所以去访问绿色层次的右子树，发现访问右子树的时候，这结点为空，所以返回了，返回给最外层。此时最外层的左子树已经访问完毕，该去访问右子树了。

2中序遍历

顺序：# 3 # 2 # 1 # 5 # 4 # 6 #

思路：先去访问左子树，再去访问根节点，最后访问右子树。访问每一个层次的时候也是遵循这样的顺序的

代码：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

递归展开图

 

黑色的数字代表访问的顺序。由于访问顺序是左子树，根，右子树，因此会一直访问左子树，左子树的左子树，左子树的左子树的左子树……一直到最后的黄色的根，为NULL，左子树访问完毕，访问根3，根访问完毕访问右子树，为NULL，返回，红色层次作为绿色层次的左子树访问完毕，访问该层右子树，为NULL，返回给最外层，到此左子树访问完毕，去访问根1，再去访问右子树，访问右子树的时候也是这个顺序

 

3 后续遍历

访问：# # 3 # 2 # # 5 # # 6 4 1

代码：

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
 
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ",root->data);
}

思路和展开图类似，不做赘述。

其实最主要的还是分析遍历返回的条件：该结点为空

三 搜索

1 该链式二叉树有多少个结点

思路一

static int count = 0;
int NodeNum(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	count++;
	NodeNum(root->left);
	NodeNum(root->right);
	return count;
}

思路一其实和前序遍历有点相似，如果遍历到的这个结点不是空节点那么就++，但是由于层层递归，保存不了每层++后的值，因此要在外部定义一个count用于存储值

思路二

int NodeNum1(BTNode* root)
{
	return root == NULL ? 0 : NodeNum1(root->left) + NodeNum(root->right) + 1;
}

思路二其实用到了分治的思想，先去看这棵树是不是空节点，如果是就返回，否则再去遍历她的左子树和右子树，结点的数量就是左子树结点的个数加上右子树结点的个数，由于该节点不为空的话，那么说明这一个结点是有效的，就++，记录下这个结点再去遍历她的左右子树

2 求叶子结点的数量

什么是叶子结点？左子树和右子树都为NULL的结点是叶子结点，只有这样子才可以计数。返回有两个条件：1 该节点为NULL 2 记录到叶子结点了

以递归左树为例子

 每一个值是通过return语句返回给上一层次的，全部叶子结点的数就是左子树叶子结点的数加上右子树叶子结点的数，以此类推，当递推到最后一层的时候，记录下对应的叶子结点的数返回给上一层次

代码

int NodeLeaf(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	
	if ((root->left && root->right)==NULL)
	{
		return 1;
	}
	return NodeLeaf(root->left) + NodeLeaf(root->right);
}

3 求某一层结点的数量

思路：求第Num层结点的数量实际上就是求改左子树和右子树Num-1层的结点数量，再然后就是求对应左右子树Num-2层的结点数量，以此类推。当到对应层的时候就要进行计数了

但是这一层有空结点就要进行判断，如果不是空结点就返回1，否则只能计0

int TreeNumLevel(BTNode* root,int num)
{
	assert(num >= 1);
 
	
	if (num == 1)
	{
		if (root == NULL)
		{
			return 0;
		}
		else
		{
			return 1;
		}
	}
 
	return TreeNumLevel(root->left, num - 1)+ TreeNumLevel(root->right, num - 1);
	
}

4 返回某个结点的data为特定值的结点

思路：最基本的还是进行遍历，如果该节点为NULL，说明遍历到头了，应该返回NULL了。遍历应该采取前序遍历效果比较好，因为如果第一个结点就是我要求的我就可以直接返回该节点了。否则还要继续遍历下去

对一个结点有两种结果：

1 该节点是我要找的结点 那么此时就一层一层返回
2 如果该节点不是要找的结点 ①已经到最后了，说明找不到，返回NULL，否则继续查找

BTNode* FindNode(BTNode* root, int data)
{
	if (root == NULL)
	{
		return NULL;
	}
 
	if (root->data == data)
	{
		return root;
	}
                              
	FindNode(root->left,data);
	FindNode(root->right,data);
 
	return NULL;
}