-
算法开篇——数组
1、数组理论基础
总结刷题顺序全部来自代码随想录
数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力也就是说，想法很简单，但实现起来可能就不是那么回事了。
数组的特点：
数组是存放在连续内存空间上的相同类型数据的集合。
举一个字符数组的例子，如图所示：
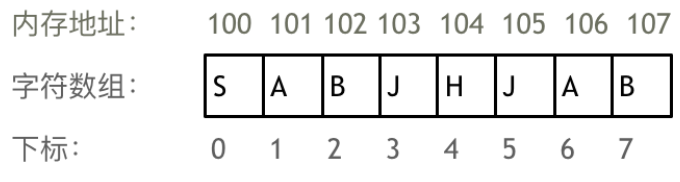
数组可以方便的通过下标索引获取到对应位置的元素。
需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：
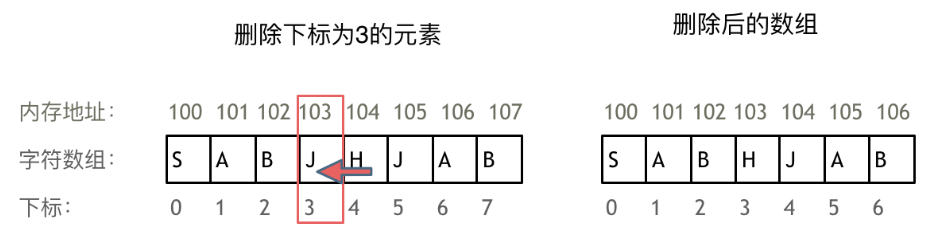
数组的元素是不能删的，只能覆盖。
二维数组
不同编程语言的内存管理是不一样的，以Java为例，在Java中二维数组不是连续分布的。
Java是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。
所以看不到每个元素的地址情况，这里我以Java为例，做一个实验。
@Test public void testArr() { int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9, 9, 9}}; System.out.println(arr[0]); System.out.println(arr[1]); System.out.println(arr[2]); System.out.println(arr[3]); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
输出的地址为：
[I@16f7c8c1 [I@2f0a87b3 [I@319b92f3 [I@fcd6521- 1
- 2
- 3
- 4
这里的数值是16进制，这不是真正的地址，而是经过处理过后的数值了，我们也可以看出，二维数组的每一行头结点的地址是没有规则的，更谈不上连续。
所以Java的二维数组可能是如下排列的方式：
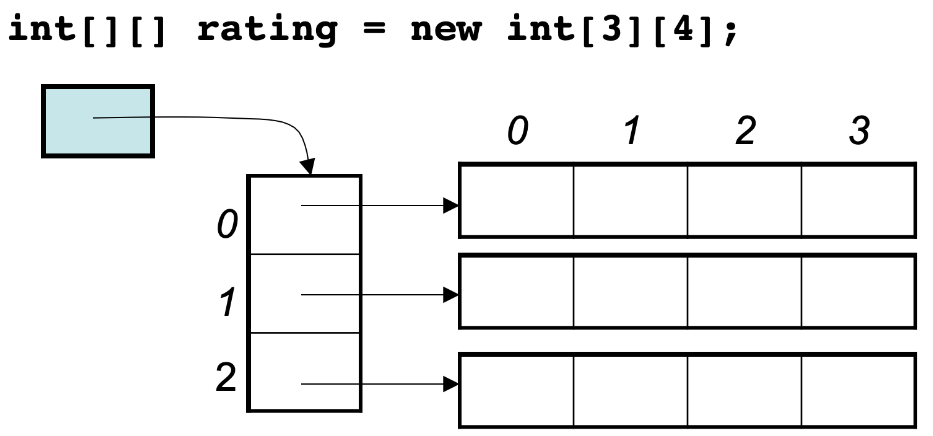
2、二分查找
704. 二分查找
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4- 1
- 2
- 3
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1- 1
- 2
- 3
提示：
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
思路
这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。
例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：
二分查找主要就是看区间中左右临界值，以及三个判断条件
首先：中间元素索引 (left + right) / 2，循环条件是什么？while(left <= right)
- if (nums[middle] == target) ，直接返回目标索引
- if (nums[middle] > target)，此时右临界，right = middle - 1
- if (nums[middle] < target)，此时左临界，right = middle + 1
代码实现
public int search(int[] nums, int target) { //target 小于nums[0] 或 大于nums[nums.length - 1]时 不存在目标元素直接返回-1 if(target < nums[0] || target > nums[nums.length - 1]){ return -1; } int left = 0; int rigth = nums.length - 1; while(left <= rigth){ //每一轮数组中中间元素索引如何得到？ int mid = (rigth + left) / 2; if(target == nums[mid]){ return mid; } else if(target < nums[mid]){ rigth = mid - 1; } else{ left = mid + 1; } } //rigth < left 说明不存在目标元素，直接返回-1 return -1; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
总结：
看到升序无重复元素数组，这类题基本都是二分查找思想来解题。（时间复杂度O(lgN)）
其他题目：
34.在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。
进阶：你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？
示例 1：
- 输入：nums = [5,7,7,8,8,10], target = 8
- 输出：[3,4]
示例 2：
- 输入：nums = [5,7,7,8,8,10], target = 6
- 输出：[-1,-1]
示例 3：
- 输入：nums = [], target = 0
- 输出：[-1,-1]
思路
以二分法为切入点，继续向左和向右继续查找目标元素
class Solution { public int[] searchRange(int[] nums, int target) { if(nums.length == 0 || target < nums[0] || target > nums[nums.length - 1]){ return new int[]{-1,-1}; } int index = binarySearch(nums, target); if(index == -1) return new int[]{-1,-1}; int left = index; int right = index; // 继续向左找 注意防止数组越界 while(left > 0 && nums[left - 1] == target){ left--; } // 向右找 while(right < nums.length - 1 && nums[right + 1] == target){ right++; } return new int[]{left, right}; } /** * 二分查找目标元素下标，不存在则返回-1 **/ public int binarySearch(int[] nums, int target){ //左右下标索引 int left = 0; int right = nums.length - 1; while(left <= right){ int mid = left + (right - left) / 2; if(nums[mid] == target){ return mid; }else if(nums[mid] > target){ right = mid - 1; }else{ left = mid + 1; } } return -1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
3、移除元素
27. 移除元素
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
思路：俗称双指针
代码实现
class Solution { public int removeElement(int[] nums, int val) { int j = 0; for(int i = 0; i < nums.length; i++){ //不满足元素跳过 if(nums[i] == val){ continue; } //跟目标元素不相等，放入数组中，下标从0开始 nums[j++] = nums[i]; } return j; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
其他题目：
844. 比较含退格的字符串
给定
s和t两个字符串，当它们分别被输入到空白的文本编辑器后，如果两者相等，返回true。#代表退格字符。注意： 如果对空文本输入退格字符，文本继续为空。
示例 1：
输入：s = “ab#c”, t = “ad#c”
输出：true
解释：s 和 t 都会变成 “ac”。
示例 2：输入：s = “ab##”, t = “c#d#”
输出：true
解释：s 和 t 都会变成 “”。
示例 3：输入：s = “a#c”, t = “b”
输出：false
解释：s 会变成 “c”，但 t 仍然是 “b”。思路：
这种匹配（消除）问题是栈的擅长所在，可以使用栈这种数据结构，解决该问题。
代码实现：
public boolean backspaceCompare(String s, String t) { return getString(s).equals(getString(t)); } public String getString(String start) { // 栈数据结构 先进后出 Stack<Character> stack = new Stack<>(); char[] chars = start.toCharArray(); for (char ch : chars) { if (ch != '#') { stack.push(ch); } else { if (!stack.isEmpty()) { //不判空，弹栈的时候可能会报错 stack.pop(); } } } return stack.toString(); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
时间复杂度、空间复杂度都是O(N)。
先用栈来解决该题，后面详细搞搞双指针，再用双指针法来解决
4、有序数组的平方
977.有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。
示例 1： 输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]
示例 2： 输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]
两种解法
比较容易理解，直接上代码：
public int[] sortedSquares(int[] nums) { //普通解法：最直观，直接把所有元素的平方直接放到数组里，再用工具类排序 // int[] res = new int[nums.length]; // for(int i = 0; i < nums.length; i++){ // res[i] = nums[i] * nums[i]; // } // Arrays.sort(res); // return res; //进阶解法：双指针法，元素平方最大应该是在两端 int[] res = new int[nums.length]; // 左到右 int left = 0; // 右到左 int right = nums.length - 1; //新数组索引下标 int index = nums.length - 1; while (left <= right) { //每次都找到元素平方最大值 if (nums[left] * nums[left] < nums[right] * nums[right]) { res[index] = nums[right] * nums[right]; right--; } else { res[index] = nums[left] * nums[left]; left++; } index--; } return res; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
5、长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
示例：
输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。
思路：
第一种：双重循环暴力解法；
第二种：滑动窗口解法，所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
代码实现：
public int minSubArrayLen(int target, int[] nums) { // // 暴力解法，理论可行但是超时了 // // 记录连续数组长度 // int length = 0; // // 记录连续数组最小长度 // int minLength = Integer.MAX_VALUE; // for(int i = 0; i < nums.length; i++){ // int sum = 0; // for(int j = i; j < nums.length; j++){ // sum += nums[j]; // if(sum >= target){ // //连续数组长度 // length = j - i + 1; // if(length < minLength){ // //满足条件记录连续数组最小长度 // minLength = length; // } // } // } // } // // 没有被赋值说明没有满足条件的连续数组 // return minLength == Integer.MAX_VALUE ? 0 : minLength; //滑动窗口 // 起始位置 int i = 0; // 记录连续数组长度 int length = 0; // 记录连续数组最小长度 int minLength = Integer.MAX_VALUE; int sum = 0; // j记录终止位置，滑动起始i的位置 for(int j = 0; j < nums.length; j++){ //sum值在原本基础上累加 sum += nums[j]; //起始位置可能持续移动，不能用if判断 while(sum >= target){ length = j - i + 1; if(length < minLength){ minLength = length; } // 移动起始位置 sum -= nums[i]; i++; } } return minLength == Integer.MAX_VALUE ? 0 : minLength; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
其他题目：
904.水果成篮
解决方案：
滑动窗口（双指针）public int totalFruit(int[] fruits) { // key：水果种类 value：对应水果数量 Map<Integer, Integer> map = new HashMap<>(); int ans = 0; // i起始位置，j终止位置，c 水果种类 for (int i = 0, j = 0, c = 0; j < fruits.length; j++) { if (!map.containsKey(fruits[j])) { map.put(fruits[j], 1); c++; } else { map.put(fruits[j], map.get(fruits[j]) + 1); } //水果种类大于2，移动起始位置 （滑动窗口） while (map.keySet().size() > 2) { map.put(fruits[i], map.get(fruits[i]) - 1); //该类水果为0，移除该类水果 if (map.get(fruits[i]) == 0) { map.remove(fruits[i]); c--; } i++; } ans = Math.max(ans, j - i + 1); } return ans; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
76.最小覆盖子串
滑动窗口
代码实现：
public String minWindow(String s, String t) { if (t.length() > s.length()) { return ""; } //统计所需字符及其数量 Map<Character, Integer> need = new HashMap<>(16); for (int i = 0; i < t.length(); i++) { need.put(t.charAt(i), need.getOrDefault(t.charAt(i), 0) + 1); } //统计窗口内的字符及其数量 Map<Character, Integer> window = new HashMap<>(16); //i,j 左右指针 int i = 0; //记录字符满足数量 int valid = 0; //记录窗口大小 int min = Integer.MAX_VALUE; //记录左下标 int left = 0; for (int j = 0; j < s.length(); j++) { char ch1 = s.charAt(j); window.put(ch1, window.getOrDefault(ch1, 0) + 1); //窗口内字符数量与所需字符数量相等 if (window.get(ch1).equals(need.get(ch1))) { valid++; } //移动左下标（移动窗口） while (valid == need.size()) { if (j - i + 1 < min) { min = j - i + 1; left = i; } char ch2 = s.charAt(i); if (window.get(ch2).equals(need.get(ch2))) { valid--; } window.put(ch2, window.get(ch2) - 1); i++; } } return min == Integer.MAX_VALUE ? "" : s.substring(left, left + min); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
6、螺旋矩阵II
59.螺旋矩阵II
给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
思路
这道题真的没什么算法，只需保证螺旋上右下左四条边的时候，保证规则是一样的就ok；因此我遵循左闭右开的原则，保证每次规则都一样，还需要想好需要循环几圈，记录每次循环开始的位置（对角线元素即每次循环起始位置）以及每次循环偏移量也会发生改变，循环圈数为
n / 2，n为偶数刚好结束，如果n为奇数，中心位置没有元素直接单独赋值即可，算法结束。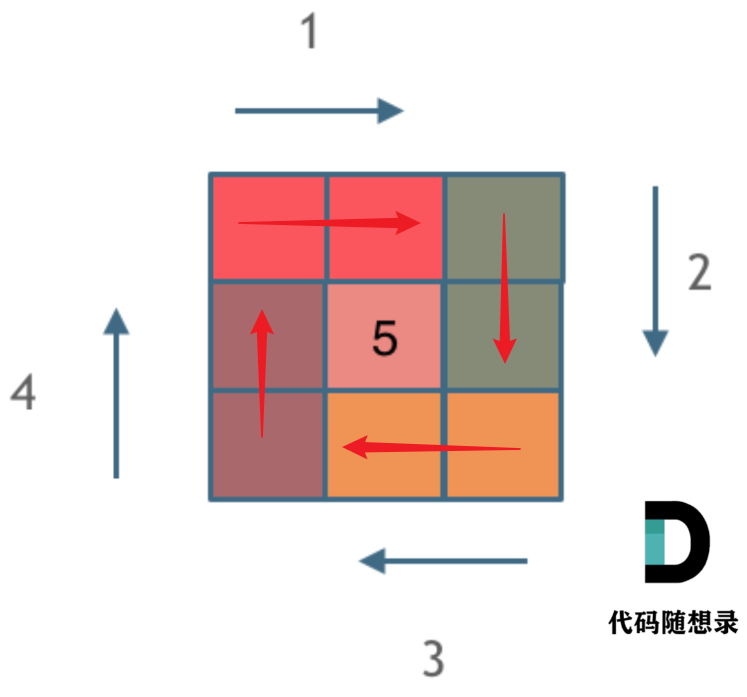
左闭右开保证每条边规律一样即可。
代码实现：
第一种解法：
public int[][] generateMatrix(int n) { int[][] ans = new int[n][n]; int num = 1; //每次转圈起始位置，对角线 int start = 0; //转圈几次，n/2 n如果是奇数，中心位置元素单独赋值 int loop = 0; int i = 0; int j = 0; int offset = 1; //顺时针 while (loop++ < n / 2) { //整体左闭右开 //上->左到右 i = start; j = start; for (; j < n - offset; j++) { ans[i][j] = num++; } //右->上到下 for (; i < n - offset; i++) { ans[i][j] = num++; } //下->右到左 for (; j > start; j--) { ans[i][j] = num++; } //左->下到上 for (; i > start; i--) { ans[i][j] = num++; } offset++; start++; } //奇数 if (n % 2 == 1) { ans[n / 2][n / 2] = n * n; } //奇数，中心位置单独处理 if (n % 2 == 1) { ans[n / 2][n / 2] = n * n; } return ans; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
第二种解法：边界法
public int[][] generateMatrix(int n) { //这次来用边界法 int[][] ans = new int[n][n]; //上下左右四个边界 int up = 0, down = n - 1, left = 0, right = n - 1; int i,j = 0; //初始值 int num = 1; while(true){ //上 for(j = left; j <= right; j++){ ans[up][j] = num++; } if(++up > down) break; //右 for(i = up; i <= down; i++){ ans[i][right] = num++; } if(--right < left) break; //下 for(j = right; j >= left; j--){ ans[down][j] = num++; } if(--down < up) break; //左 for(i = down; i >= up; i--){ ans[i][left] = num++; } if(++left > right) break; } return ans; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
其他题目：
54.螺旋矩阵
思路
与上一题矩阵不同的是，这个矩阵不是方形矩阵，没有特别规律可循，可以使用边界法（比较好懂）
代码实现：
public List<Integer> spiralOrder(int[][] matrix) { int m = matrix.length; int n = matrix[0].length; List<Integer> res = new ArrayList<>(); //边界法：定上下左右四个边界，每处理一条边边界向着相反方向移动 //直到有边界越界结束循环 int up = 0, down = m - 1, left = 0, right = n - 1; int i, j = 0; while(true){ //上边界 for(j = left; j <= right; j++){ res.add(matrix[up][j]); } //上边界向下移 if(++up > down) break; //右边界 for(i = up; i <= down; i++){ res.add(matrix[i][right]); } //右边界向左移 if(--right < left) break; //下边界 for(j = right; j >= left; j--){ res.add(matrix[down][j]); } //下边界向上移 if(--down < up) break; //左边界 for(i = down; i >= up; i--){ res.add(matrix[i][left]); } //左边界向右移 if(++left > right) break; } return res; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
7、总结
在面试中，数组是必考的基础数据结构。其实数组的题目在思想上一般是比较简单的，但是如果想高效，并不容易。
下面是数组类题目常用解题方法：
二分法
前提：有序无重复元素数组
遵循循环不变量原则，从中间索引开始，向左或向右处理
双指针法
双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
相向双指针法：一个指针从左向右，一个指针从右向左，找到满足条件的元素进行操作，直到左指针大于右指针循环结束。
滑动窗口法
滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
核心三点，需要想清楚：
- 窗口内是什么？
- 如何移动窗口的起始位置？
- 如何移动窗口的结束位置？
（一般都是先移动末尾指针，满足窗口条件在移动起始指针）
数组总结如下：
-
相关阅读:
LeetCode 第3题：无重复字符的最长子串（Python3解法）
AI产品经理 | 入行AI大模型的必备知识
git操作的一些解答，后续根据问题进行更新
jvm04
多线程进阶：Callable和JUC的常见类
代码随想录算法训练营第五十八天| 583. 两个字符串的删除操作 72. 编辑距离
Stimulsoft Reports.NET 2022.4.3 for WinForms
SpringMVC的拦截器（Interceptor）
【LeetCode】用队列实现栈和用栈实现队列（C语言）
python 检测文本语言类型
- 原文地址：https://blog.csdn.net/qq_43417581/article/details/127589377
