【C语言】全面解析数据在内存中的存储

前言

C语言中有char、short、int、long、long long、float和doubole这些数据类型。这些数据类型也叫内置类型。
所占存储空间的大小：

类型的基本分类

整型

整型一共有char、int、short、long和long long这五种类型。
char类型的数据在内存中存放的是ASCII码值，是整型，所以也被当成整型。
这些整型都分为有符号的整型和无符号的整型，具体可以看下面：

	int a = 5;
	signed int b;//有符号的整型
	unsigned int c;//无符号的整型
1
2
3

signed是有符号的，unsigned是无符号的。
平时我们定义变量时，一般都不会加前面，只是int 变量名 = 数据，其实这就相当于signed int 变量名 = 数据。
$注意$ ：但是char这个类型比较特殊，在C语言的标准中，没有定义char到底是有符号的还是无符号的，取决于编译器。
关于无符号和无符号：
前面我们说到了int类型在内存中占4个字节，1个字节就是8个bit。

比特位即bit，是计算机最小的存储单位。以0或1来表示比特位的值(二进制表示)。

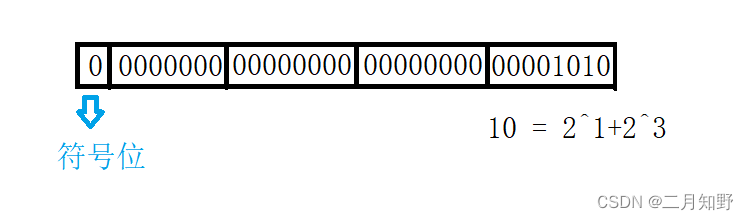
10的二进制序列就如图所示，其中第一位是符号位，0代表正数，1代表负数

浮点数

浮点数有float和double，一般用来表示小数。
float的表示精度低，存储数值范围较小。
double的表示精度高，存储数值范围较大。

自定义类型

自定义类型有数组类型、结构体类型、枚举、联合体、指针类型和空类型(void)。在这就不一一详细讲了。

整型在内存中的存储

在了解整型在内存中的存储前，先了解一个计算机的原码、反码、补码。

原码、反码、补码

数值表示形式有：二进制、八进制、十进制和十六进制。
整数的二进制也有三种表达形式：原码、反码、补码。
整数中：
正数的原码反码补码相同
负数的原码反码补码是需要计算的

原码：整数的二进制序列（注意符号位）
反码：符号位不变，其它位按位取反就是反码（0变1，1变0）
补码：反码加1就是补码

整型在内存中存放的是补码

接下来来验证内存中存放的是补码：

我定义了一个a变量，值为-10. 原码反码和补码也给大家了，因为正整数的原码、反码和补码相同，所以不用正整数验证。接下来让我们来用编译器来调试并监视来观察内存，来看看整型在内存中是如何存储的。

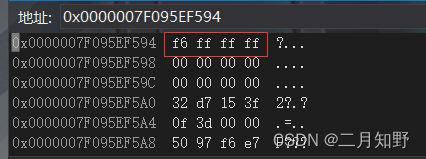
看上图，虽然这里面看到的是十六进制，但不要认为是以十六进制存储的，但本质存的还是二进制序列。由此我们可以得出内存中存放的是补码。

大端和小端

我们看到上图a的地址和我们写的十六进制序列是反着的，为什么？这就是大小端的问题了。

大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址
中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地
址中。

如何判断编译器是大端还是小端

int main()
{
	int a = 1;
	if(*(char*)&a == 1)
	{
		printf("小端")
	}
	else
	{
		printf("大端")
	}
}
1
2
3
4
5
6
7
8
9
10
11
12

如果是小端存储存储的顺序应该是01 00 00 00 大端的话是00 00 00 01
我们对a进行取地址，然后强转成char类型的指针然后再进行解引用，因为强制类型转换了，所以只能访问1个字节的地址，如果得到的1就是小端，0就是大端。

浮点数在内存中的存储

根据国际标准IEEE（电气和电子工程协会）754，一个浮点数 (Value) 的表示其实可以这样表示：

也就是浮点数的实际值，等于符号位（sign bit）乘以指数偏移值(exponent bias)再乘以分数值(fraction)。

简单来说就是对于浮点数在内存中的存储，无论是float（32位浮点数）还是double（64）位浮点数(S)，都有符号位(Exp)，指数位和有效数字位(Fraction)。

对于float这种32位浮点数来说，指数位占8个bite位，有效数字位占23个bite位
对于double这种64位浮点数来说，指数位占11个bite位，有效数字位占52个bite位
符号位都是占1个bite位。
其中因为浮点数的小数部分，用二进制中难以存储，就会存在精度不准的问题。

单精和双精浮点数的有效数字分别是有存储的23和52个位，加上最左手边没有存储的第1个位，即是24和53个位。

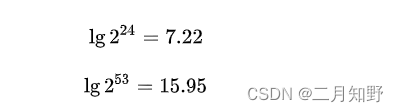
由以上的计算，单精和双精浮点数可以保证7位和15位十进制有效数字。

总结

对于数据在内存中的存储，大家还是要重点掌握原码、反码和补码的，要会计算，然后是浮点数的存储方式，可以把它当成一个拓展知识来了解，拓展一下眼界，如果真要熟练掌握浮点数的存储规则是要研究很多东西的，大家感兴趣也可以去看一下国际标准IEEE754。