-
sklearn 笔记 SVM
1 分类任务
1.1 SVC
- 拟合时间至少是样本数量的二次方关系
- ——》大数据集,可以考虑LinearSVC
1.1.1 基本使用方法
- sklearn.svm.SVC(
- C=1.0,
- kernel='rbf',
- degree=3,
- gamma='scale',
- coef0=0.0,
- shrinking=True,
- probability=False,
- tol=0.001,
- cache_size=200,
- class_weight=None,
- verbose=False,
- max_iter=-1,
- decision_function_shape='ovr',
- break_ties=False,
- random_state=None)
1.1.2 主要参数说明
C L2正则化参数 kernel {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable
算法中使用的kernel
degree 如果kernel是poly的时候,多项式的级数 gamma kernel是rbf、poly、sigmoid时的γ coef0 kernel时poly和sigmoid时的r probability 是否启用概率估计。
这必须在调用 fit 之前启用,这会减慢该方法,因为它在内部使用 5 折交叉验证,并且 predict_proba 可能与 predict 不一致。
decision_function_shape {‘ovo’, ‘ovr’}
如果是多类分类的话,ovo是两两比较 one vs one;ovr是一个和其他的比较 one vs rest
class_weight 每个类设置不同的惩罚参数 1.1.3 举例
- import numpy as np
- from sklearn.svm import SVC
- X = np.array([[-3, -7], [-2, -10], [1, 1], [2, 5]])
- y = np.array([1, 1, 2, 2])
- #数据部分
- clf=SVC(kernel='linear')
- clf.fit(X, y)
- #fit数据
- clf.predict([[-0.8, -1]])
- #array([2])
- x=np.linspace(-3,2,50)
- a,b=clf.coef_[0]
- w=clf.intercept_
- y=(-a*x-w)/b
- import matplotlib.pyplot as plt
- plt.scatter(X[:,0],X[:,1],c=Y)
- plt.plot(x,y)

1.1.4 类属性
classes_ 类的label
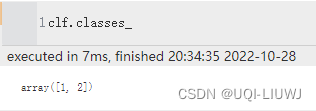
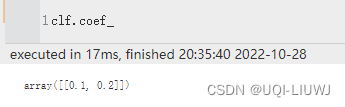
class_weight 各个类的penalty C的数值 coef_ 如果kernel是“linear',返回w
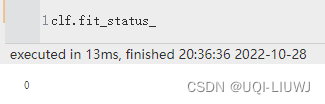
fit_status_ 是否正确fit,0正确1不正确
intercept_ 截距

n_features_in_ 输入的feature 维度 support_ 输入X中,是支持向量的那些向量的坐标

support_vectors_ 支持向量

n_support_ 每个类中支持向量的个数

1.1.5 类函数
fit(X,Y) get_params 
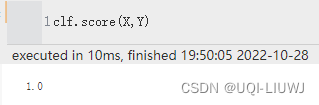
predict(X) score(X,Y) 给定数据集和label的平均准确度
decision_function(X) X中的样本在不同分类器上的评估结果
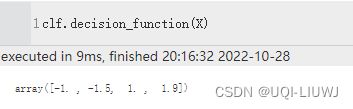
X的四个样本在分类器上得到的结果,前两个小于等于-1,所以分到一类;后两个大于等于1,所以分到另一类
1.2 NuSVC
大体上和SVC类似,这里多了一个参数来控制支持向量的数量
1.2.1 主要参数说明
除了第一个nu和SVC一样
nu 支持向量比例的下限 kernel {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable
算法中使用的kernel
degree 如果kernel是poly的时候,多项式的级数 gamma kernel是rbf、poly、sigmoid时的γ coef0 kernel时poly和sigmoid时的r probability 是否启用概率估计。
这必须在调用 fit 之前启用,这会减慢该方法,因为它在内部使用 5 折交叉验证,并且 predict_proba 可能与 predict 不一致。
decision_function_shape {‘ovo’, ‘ovr’}
如果是多类分类的话,ovo是两两比较 one vs one;ovr是一个和其他的比较 one vs rest
class_weight 每个类设置不同的惩罚参数 1.2.2 举例
- import numpy as np
- from sklearn.svm import NuSVC
- X = np.array([[-3, -7], [-2, -10], [1, 1], [2, 5]])
- y = np.array([1, 1, 2, 2])
- #数据部分
- clf=NuSVC(kernel='linear')
- clf.fit(X, y)
- #fit数据
- print(clf.predict([[-0.8, -1]]))
- #array([2])
- x=np.linspace(-3,2,50)
- a,b=clf.coef_[0]
- w=clf.intercept_
- y=(-a*x-w)/b
- import matplotlib.pyplot as plt
- plt.scatter(X[:,0],X[:,1],c=Y)
- plt.plot(x,y)

1.2.3 类属性
和SVC一样
classes_ 类的label

class_weight 各个类的penalty C的数值 coef_ 如果kernel是“linear',返回w

fit_status_ 是否正确fit,0正确1不正确

intercept_ 截距

n_features_in_ 输入的feature 维度 support_ 输入X中,是支持向量的那些向量的坐标

support_vectors_ 支持向量

n_support_ 每个类中支持向量的个数

1.2.4 类函数
和SVC一样
fit(X,Y) get_params 
predict(X) score(X,Y) 给定数据集和label的平均准确度

decision_function(X) X中的样本在不同分类器上的评估结果

X的四个样本在分类器上得到的结果,前两个小于等于-1,所以分到一类;后两个大于等于1,所以分到另一类
1.3 多类分类
- SVC 和 NuSVC 实现了多类分类的“ovo”方法(一对一,one vs one)。
- 总共构建了 n_classes * (n_classes - 1) / 2 个分类器,每个分类器训练来自两个类的数据。
- 同时,通过设置decision_function_shape 选项,可以将ovo的分类结果转换成ovr(一对其他,one vs rest)的分类结果。
- X = [[0], [1], [2], [3]]
- Y = [0, 1, 2, 3]
- clf = SVC(decision_function_shape='ovo')
- clf.fit(X, Y)
- clf.decision_function([[1]]).shape
- # (1, 6)
- #[1]在六个分类器上的结果,两两比较,一共6=4*(4-1)/2
- clf = SVC(decision_function_shape='ovr')
- clf.fit(X, Y)
- clf.decision_function([[1]]).shape
- # (1, 4)
- # #[1]在四个分类器上的结果,每个类和其他
1.4 各类不平衡问题
如果各个类数量不均,那该如何是好呢

- SVC中提供了class_weight,作为fit的一个参数
- 这是一个{class_label:value}形式的字典,其中每个value都是大于0的浮点数
- value是这个类的L2正则项系数
- sample_weight参数会将第i个样例的penalty设置成C*sample_weight[i]
2 Regression
- 支持向量分类的方法可以扩展到解决回归问题。这种方法称为支持向量回归。
- SVR和NuSVR类比SVC和NuSVC
2.1 SVR
2.1.1 主要参数
kernel {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable
算法中使用的kernel
degree 如果kernel是poly的时候,多项式的级数 gamma kernel是rbf、poly、sigmoid时的γ coef0 kernel时poly和sigmoid时的r probability 是否启用概率估计。
这必须在调用 fit 之前启用,这会减慢该方法,因为它在内部使用 5 折交叉验证,并且 predict_proba 可能与 predict 不一致。
decision_function_shape {‘ovo’, ‘ovr’}
如果是多类分类的话,ovo是两两比较 one vs one;ovr是一个和其他的比较 one vs rest
class_weight 每个类设置不同的惩罚参数 2.1.2 举例
- from sklearn.svm import SVR
- from sklearn.pipeline import make_pipeline
- from sklearn.preprocessing import StandardScaler
- import numpy as np
- n_samples, n_features = 10, 5
- y = rng.randn(n_samples)
- X = rng.randn(n_samples, n_features)
- regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
- regr.fit(X, y)
2.1.3 类属性
和SVC一样
classes_ 类的label

class_weight 各个类的penalty C的数值 coef_ 如果kernel是“linear',返回w

fit_status_ 是否正确fit,0正确1不正确

intercept_ 截距

n_features_in_ 输入的feature 维度 support_ 输入X中,是支持向量的那些向量的坐标

support_vectors_ 支持向量

n_support_ 每个类中支持向量的个数

2.1.4 类函数
和SVC一样
fit(X,Y) get_params 
predict(X) score(X,Y) 给定数据集和label的平均准确度

decision_function(X) X中的样本在不同分类器上的评估结果

X的四个样本在分类器上得到的结果,前两个小于等于-1,所以分到一类;后两个大于等于1,所以分到另一类
3 各种kernel
linear polynomial rrbf sigmoid 3.1 自实现kernel
- import numpy as np
- from sklearn import svm
- def my_kernel(X, Y):
- return np.dot(X, Y.T)
- clf = svm.SVC(kernel=my_kernel)
4 其他TIps

4.1 设置C
- C 默认为 1,这是一个合理的默认选择。
- 如果有很多noise,你应该减少它
- 减少 C 对应于更多的正则化。
- LinearSVC和LinearSVR在C变大时对C的敏感性降低,达到一定阈值后预测结果停止改善。 同时,较大的 C 值将需要更多的时间来训练,有时甚至要长 10 倍
4.2 对数据尺度进行调整
- SVM算法不是尺度不变的,因此强烈建议对数据进行scale操作。
- 例如,将输入向量 X 上的每个属性缩放为 [0,1] 或 [-1,+1],或将其标准化为均值 0 和方差 1。
- 注意,必须将相同的缩放比例应用于测试向量以 获得有意义的结果。
- 这可以通过使用pipeline轻松完成:
- from sklearn.pipeline import make_pipeline
- from sklearn.preprocessing import StandardScaler
- from sklearn.svm import SVC
- clf = make_pipeline(StandardScaler(), SVC())
-
相关阅读:
华为机试 - 城市聚集度
Intel System Flags and Fields in the EFLAGS Register
基于布谷鸟算法优化的lssvm回归预测-附代码
数据结构初阶--双向循环链表(讲解+类模板实现)
java计算机毕业设计web开发数码产品推荐平台系统设计与实现MyBatis+系统+LW文档+源码+调试部署
人脸比对CNN设计
提取字母后数字
清除aws 亚马逊cdn的缓存
搭建java部署环境以及部署Web项目到Linux
Java安全—CommonsCollections7
- 原文地址:https://blog.csdn.net/qq_40206371/article/details/127577524
