simulink求解器选择的小tip

在使用simulink时有一天我发现，对于一个很简单的信号源$\sin x$，使用两个微分模块$\frac{\Delta u}{\Delta t}$，再使用两个积分模块$\frac{1}{s}$后，得到的结果竟然与原函数不一样：

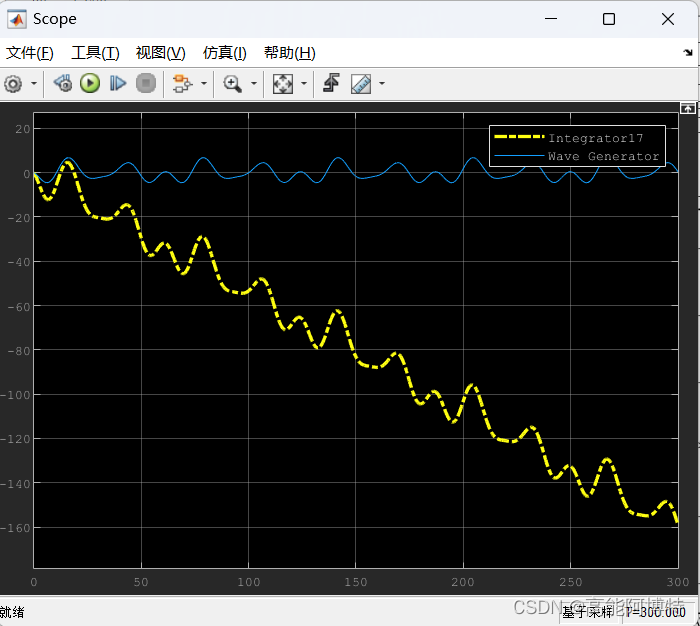
不过很快就能反应过来，如果把原函数展开为泰勒形式$f={\sum }_{i=1}^N{a}_{i}t$，那么每积分一次，就少了一个时间项，而积分回去的时候需要设置正确的积分初值才能得到正确的结果。

以二次函数为例：
$$f\left(t\right)=a{t}^2+bt+c\text{\hspace{1em}(1)}$$其二阶导：
$$\ddot{f}=2a\text{\hspace{1em}(2)}$$此时若把(2)积分回去，就有
$$f_1=a{t}^2+k_{1}t+k_2\text{\hspace{1em}(3)}$$而往往simulink的求解器中$k_1,k_2$是在积分模块$\frac{1}{s}$中设置的，若设置不正确或直接设置成了0，那么积分结果就与原函数有着天壤之别。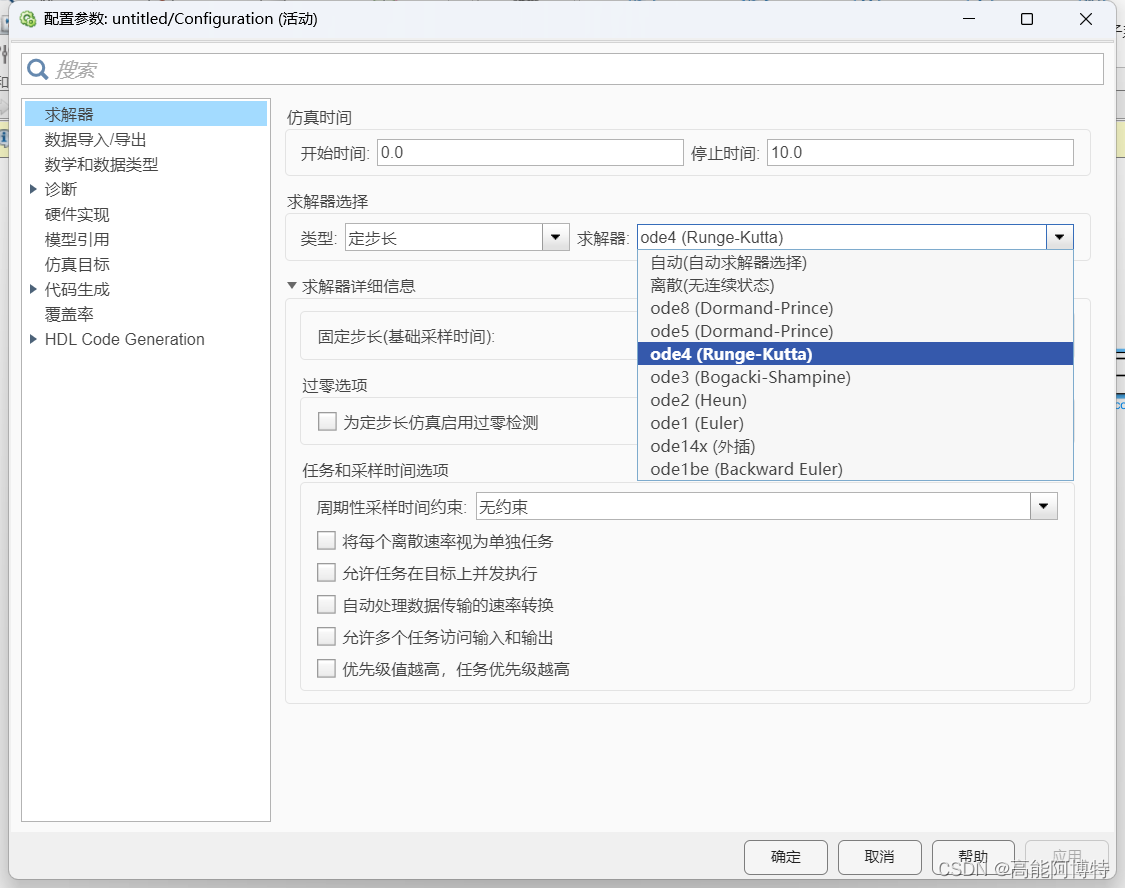

在此，笔者发现了一种避免积分结果受初值影响的办法：修改求解器。在simulink设置中的求解器在更改为定步长fixed-steps之后，可以手动选择需要的求解器。经过尝试，ode2、ode1 (Euler)、ode1be三个修改器可以做到积分无误差：

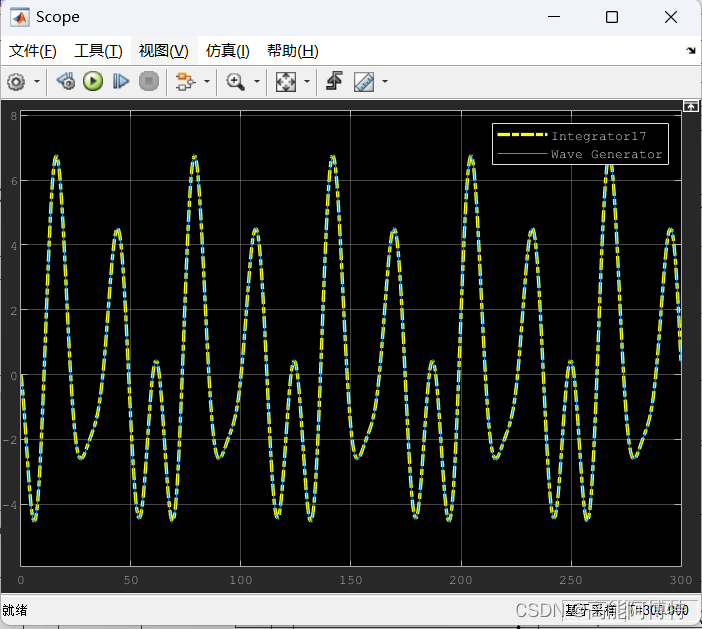
而其他求解器都或多或少有着由于积分初值引起的误差。

因此，在求解模型时，建议在定步长fixed-steps下，选择上述三种求解器进行求解。

另一方面，变步长选项下的所有求解器均不能得到好的结果。因此，为了控制误差，建议选择定步长。