LeetCode·每日一题·907.子数组的最小值之和·动态规划

作者：小迅
链接：https://leetcode.cn/problems/sum-of-subarray-minimums/solutions/1931167/dong-tai-gui-hua-dan-diao-zhan-zhu-shi-c-n9k7/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处 

题目

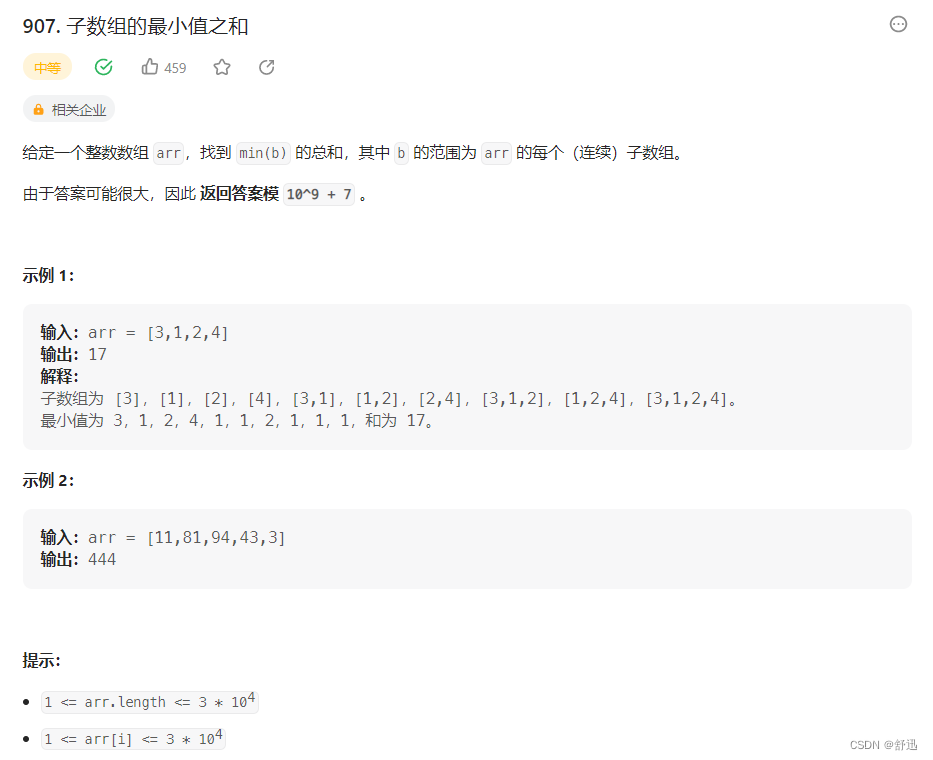
思路

题意 -> 每一个子数组中最小值的总和

暴力求解

看到题目想到的最简单的方法就是枚举所有子数组同时将所有子数组的最小值总和

动态规划优化

上述方法中我们需要对数组遍历两次，一次控制左边界 ，一次控制右边界，从而取最小值，可以使用动态规划优化，定义dp数组，其中dp[i]表示第i个数的子数组min的总和。

我们最容易想到就是直接维护子数组，并且枚举每一个子数组取最小值，可以换个思维，考虑 arr[i] 能辐射(当前值能让前面的哪些子数组取自身)的子数组有哪些，那么存在多少个子数组则当前元素的 贡献值为 n * arr[i]，那么 n之前的哪些子数组的贡献值呢？ -> dp[i-n]，别忘了dp数组的含义 ，所有 dp[i] = j*arr[i] + dp[i-j]。

例：arr=[3, 1, 2, 4], 假设dp[i]为第i个数的子数组min的总和

• dp[0]=3
• dp[1]={1,{3,1}}={1,1}=2x1+0=2
• dp[2]={2, {1, 2}, {3, 1, 2}} ={2,1,1}=1x2+dp[1]=4
• dp[3]={4, {2, 4}, {1, 2, 4}, {3, 1, 2, 4}}={4,2,1,1}=1x4+dp[2]=8

那么怎么样才能快速找到 i 能到达的最大辐射区域呢?

• 最简单的办法为暴力枚举 i 之前的所有元素，寻找第一个比 i 小的元素
• 使用单调栈，维护数组中元素的大小关系， 快速查找第一个比自己小的元素

代码

 
int sumSubarrayMins(int* arr, int arrSize){
    int dp[arrSize];
    int stack[arrSize];
    int top = -1;
    int count = 0;
    int mod = 1e9 + 7;//初始化变量
    for(int i = 0; i < arrSize; i++)
    {
        while(top != -1 && arr[stack[top]] > arr[i])//单调栈维护大小关系
            top--;
        int number = top == -1 ? (i+1) : (i-stack[top]);//取自身能辐射的最大区域
        dp[i] = number * arr[i] + (top == -1 ? 0 : dp[i-number]);//子数组min的总和
        count = (count + dp[i]) % mod;//累加 
        stack[++top] = i;
    }
    return count;
}
 
作者：小迅
链接：https://leetcode.cn/problems/sum-of-subarray-minimums/solutions/1931167/dong-tai-gui-hua-dan-diao-zhan-zhu-shi-c-n9k7/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 
class Solution {
public:
    int sumSubarrayMins(vector<int>& arr) {
        int mod = 1e9 + 7;
        int count = 0;
        vector<long> dp;
        dp.resize(arr.size());
        stack<int> stack;
        for(int i = 0; i < arr.size(); ++i)
        {
            while(!stack.empty() && arr[stack.top()] > arr[i])
            {
                stack.pop();
            }
            int number = stack.empty() ? (i+1) : (i-stack.top());
            dp[i] = number*arr[i] + (stack.empty() ? 0 : dp[i-number]);
            count = (count + dp[i]) % mod; 
            stack.push(i);
        }
        return count;
    }
 
};
 
作者：小迅
链接：https://leetcode.cn/problems/sum-of-subarray-minimums/solutions/1931167/dong-tai-gui-hua-dan-diao-zhan-zhu-shi-c-n9k7/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。