【复杂网络】网络科学导论学习笔记-第五章节点重要性与相似性

节点重要性与相似性

 本章要点

• 无向网络节点重要性排序指标:度值、介数、接近数、h-壳值、特征向量
• 有向网络节点重要性排序算法:HITS 算法和 PageRank算法
• 节点相似性与链路预测

1 无向网络节点重要性指标 

1.1 度中心性 

在社会网络分析中，常用“中心性(Centrality)"来判断网络中节点重要性或影响力。最直接的度量是度中心性(Degrree centrality)，即一个节点的度越大就意味着这个节点越重要。

这一指标背后的假设是：重要的节点就是拥有许多连接的节点。你的社会关系越多，你的影响力就越强。

度一个包含N个节点的网络中，节点最大可能的度值为N–1

度越多的节点越重要

 

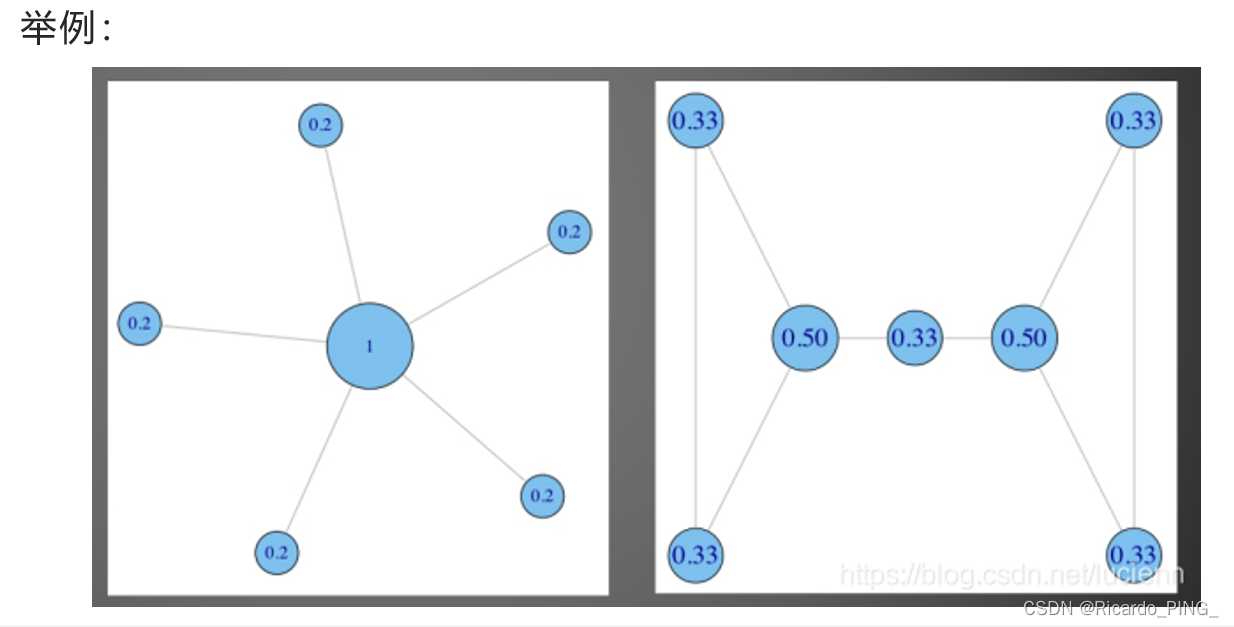
 1.2 介数中心性

从每块中的任一节点到其他某块中的任一节点的最短路径必然要经过节点H。

这种以经过某个节点的最短路径的数目来刻画节点重要性的指标就称为介数中心性(Betweeness centrality)，简称介数(BC)。

也就是说，计算网络中任意两个节点的所有最短路径，如果这些最短路径中很多条都经过了某个节点，那么就认为这个节点的介中心性高。

 

 

 

 

 

 

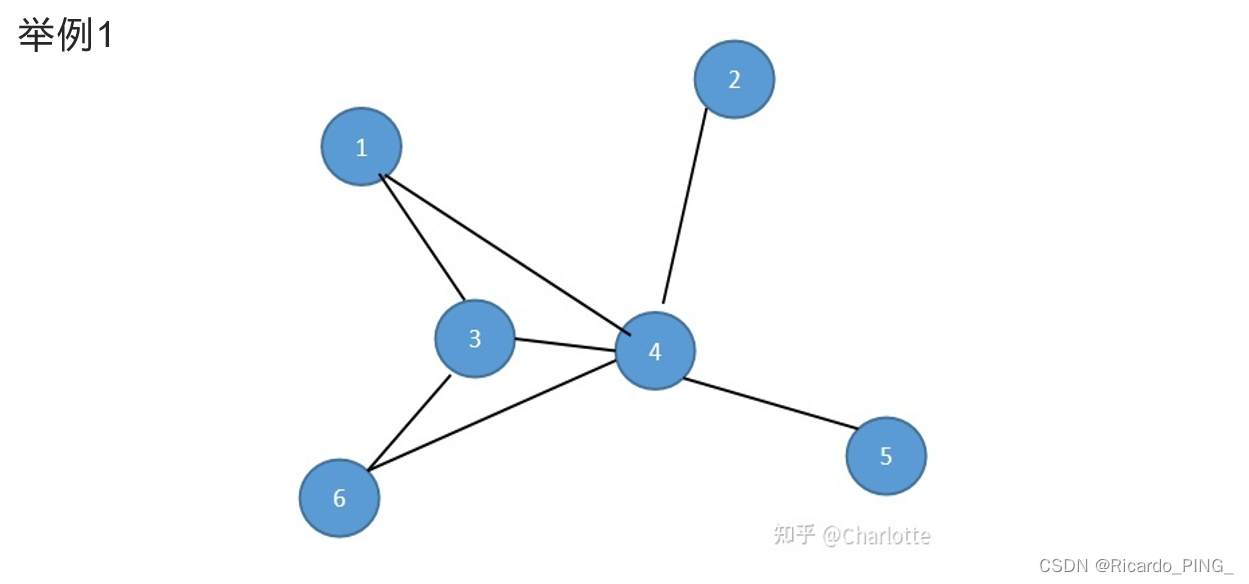
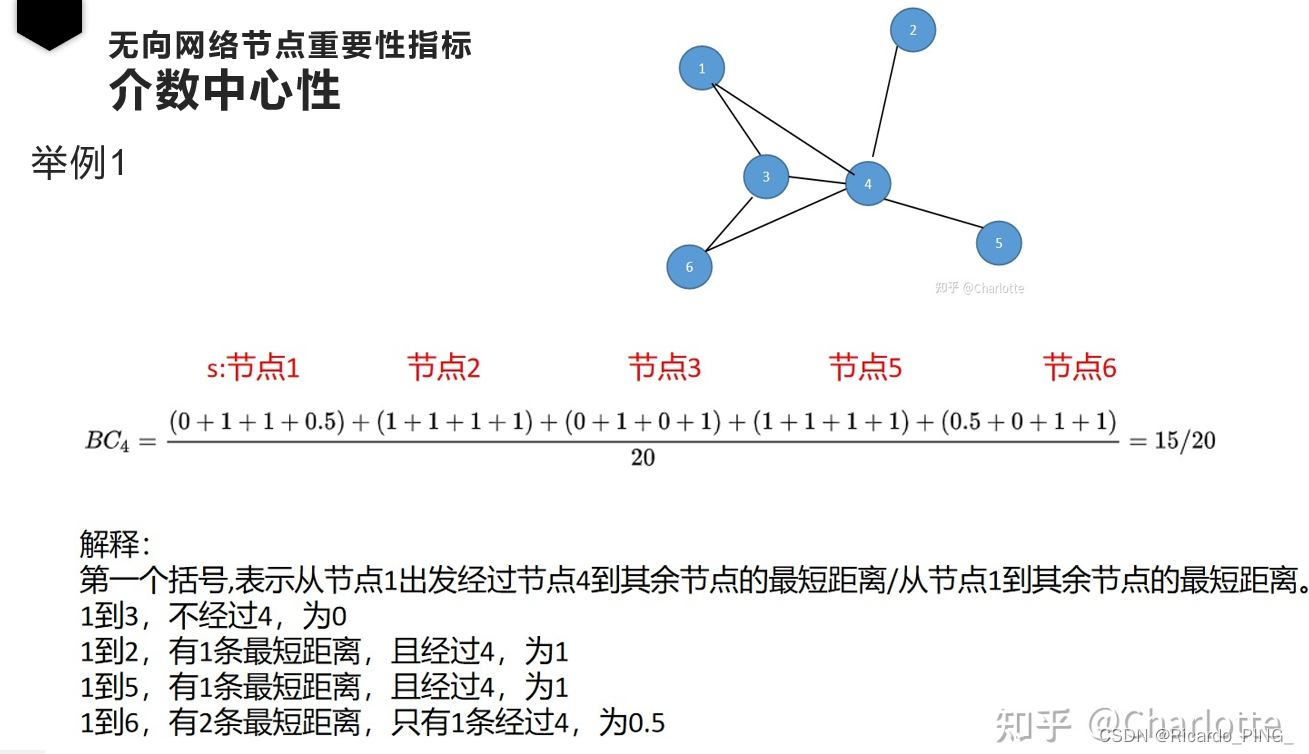
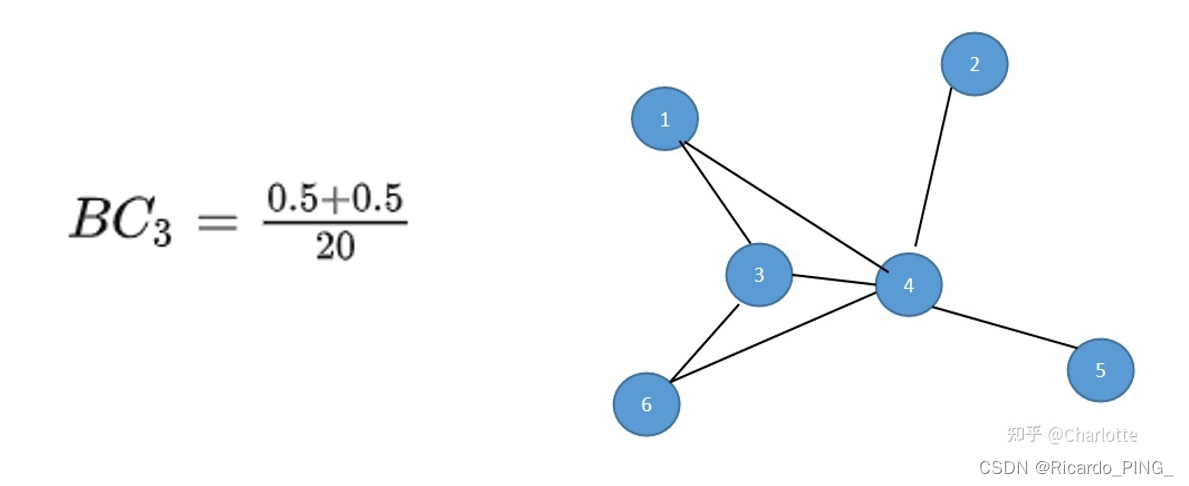
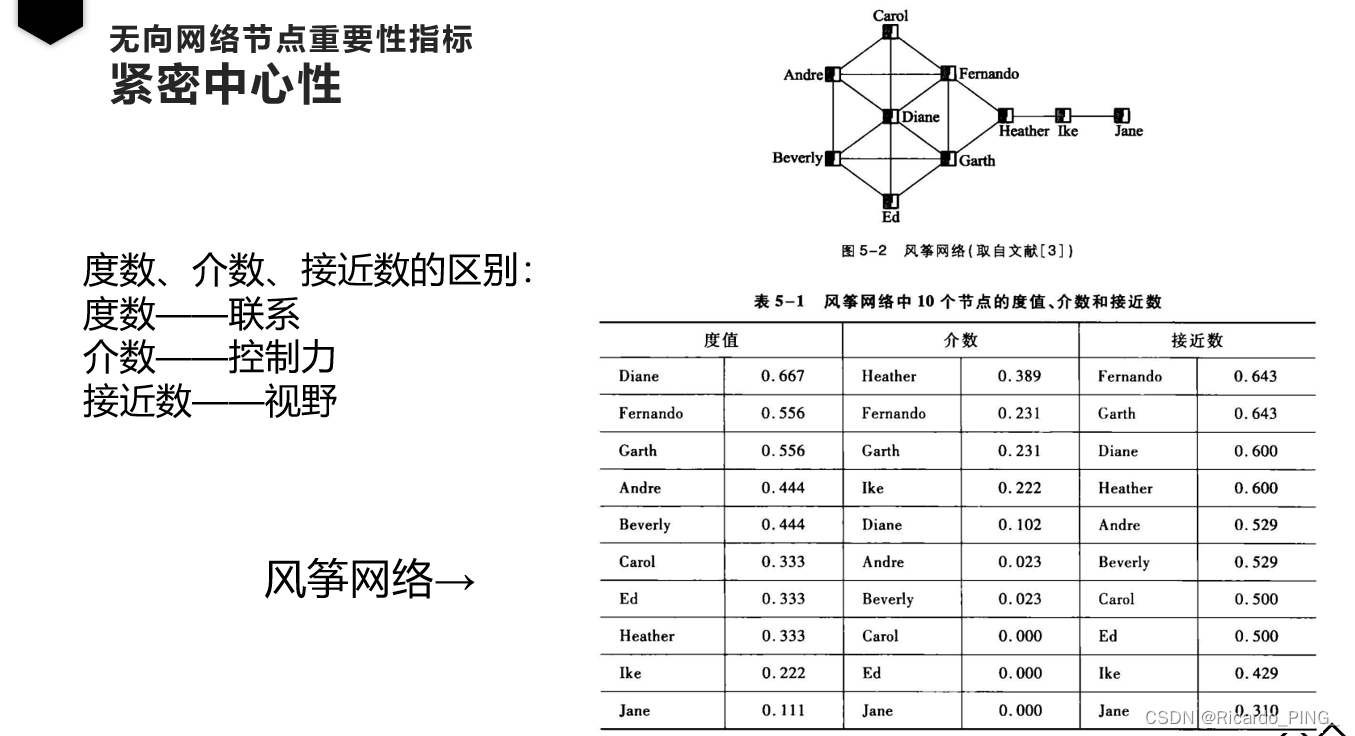
 1.3 接近中心性

度中心性仅仅利用了网络的局部特征，即节点的连接数有多少，但一个人连接数多，并不代表他/她处于网络的核心位置。

紧密中心性和中介中心性一样，都利用了整个网络的特征，即一个节点在整个结构中所处的位置。

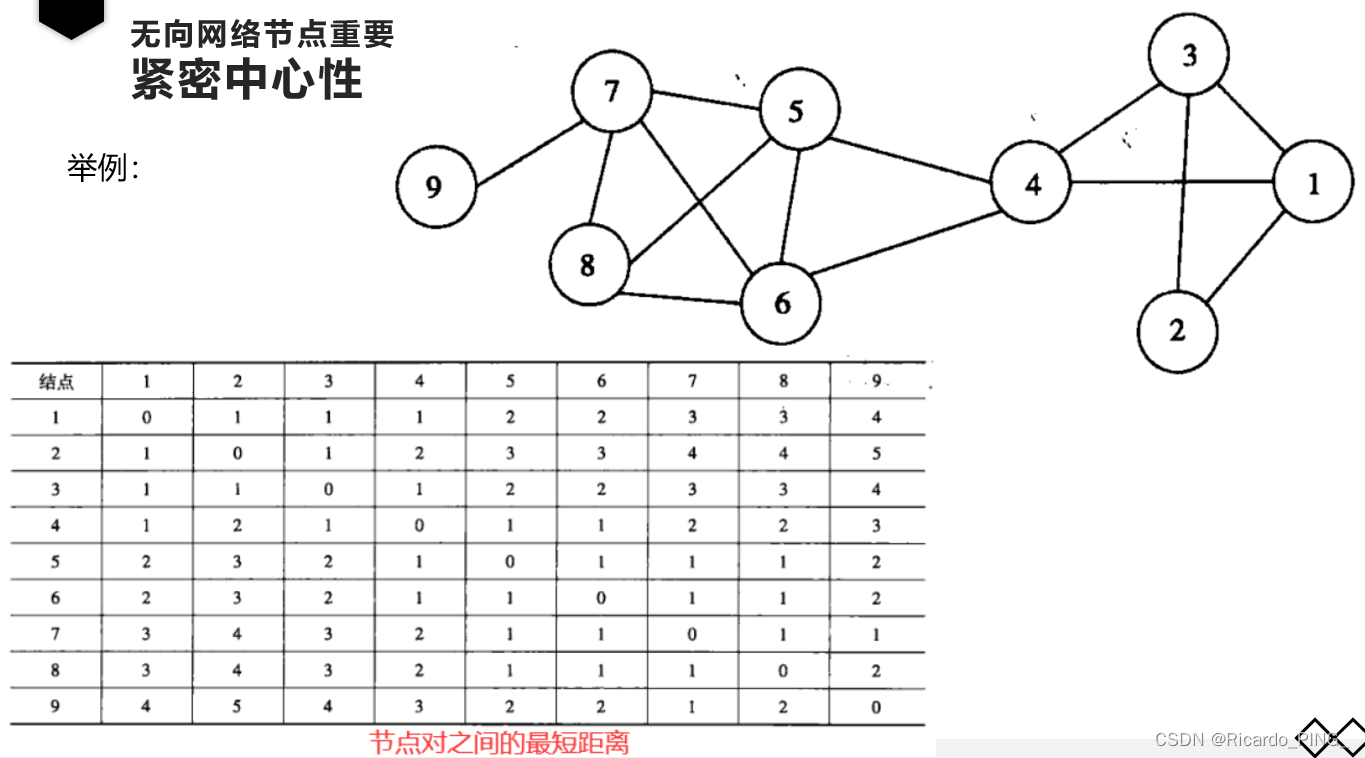
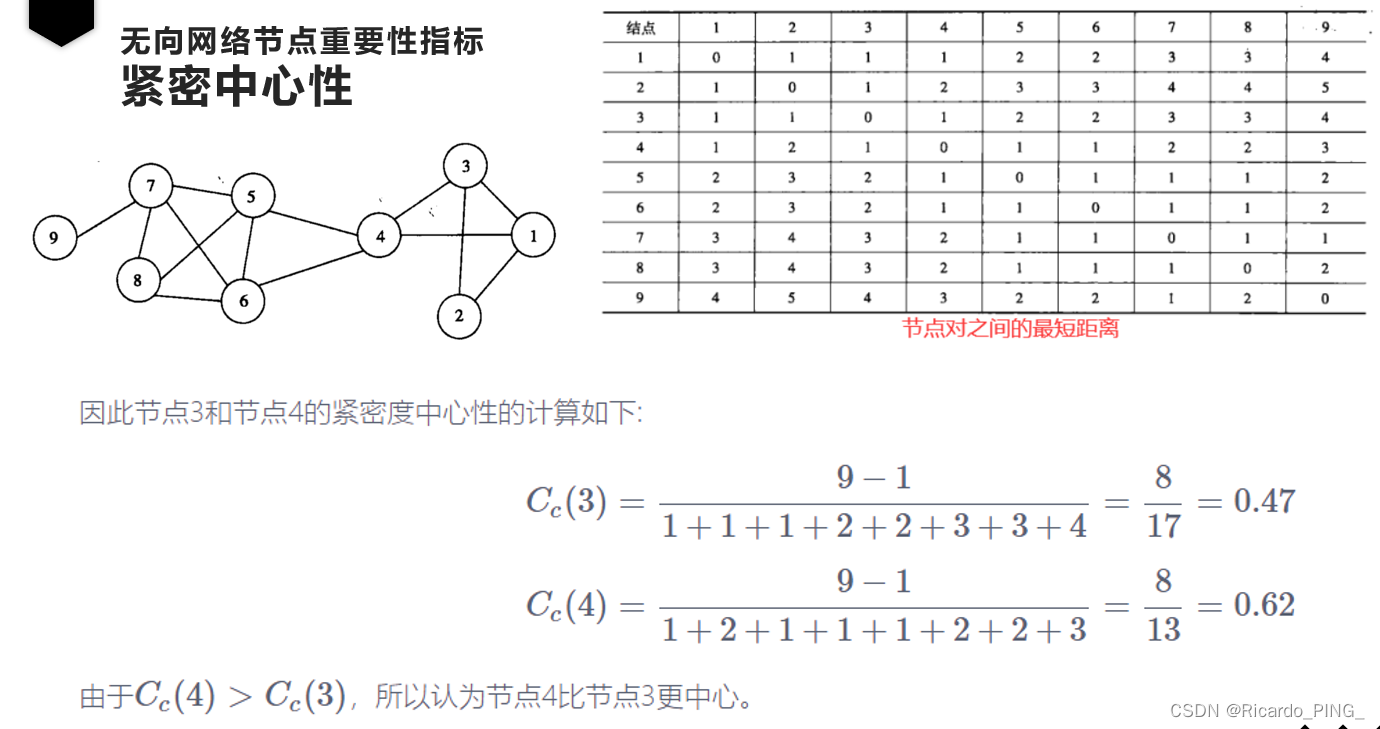
紧密度中心性与非中心结点相比，一个中心结点应该能更快地到达网络内的其他结点。

即：如果节点到图中其他节点的最短距离都很小，那么它的接近中心性就很高。相比中介中心性，接近中心性更接近几何上的中心位置。

 

 

 

 1.4 k-壳与k-核

一种粗粒化的节点重要性分类方法，即k-壳分解方法(K-shelldecomposition method )。

不妨假设网络中不存在度值为0的孤立节点。这样从度中心性的角度看，度为1的节点就是网络中最不重要的节点。

如果我们把所有度值为Ⅰ的节点以及与这些节点相连的边都去掉会怎么样？

这时网络中可能又会出现一些新的度值为1的节点，我们就再把这些节点及其相连的边去掉，重复这种操作，直至网络中不再有度值为1的节点为止。

这种操作形象上相当于剥去了网络的最外面一层壳，

我们就把所有这些被去除的节点以及它们之间的连边称为网络的1-壳(1-shell)。

有时，网络中度为 0 的孤立节点也称为 0-壳(0-shell)。

在剥去了 1-壳 后的新网络中的每个节点的度值至少为2。

接下来我们可以继续剥壳操作，即重复把网络中度值为2的节点及其相连的边去掉直至不再有度值为2的节点为止。

我们把这一轮所有被去除的节点及它们之间的连边称为网络的2-壳(2-shell)。

依次类推，可以进一步得到指标更高的壳，直至网络中的每一个节点最后都被划分到相应的k-壳中，就得到了网络的k-壳分解。

网络中的每一个节点对应于唯一的 k-壳 指标Ks，并且 Ks-壳 中所包含的节点的度值必然满足 k≥Ks。

 

 

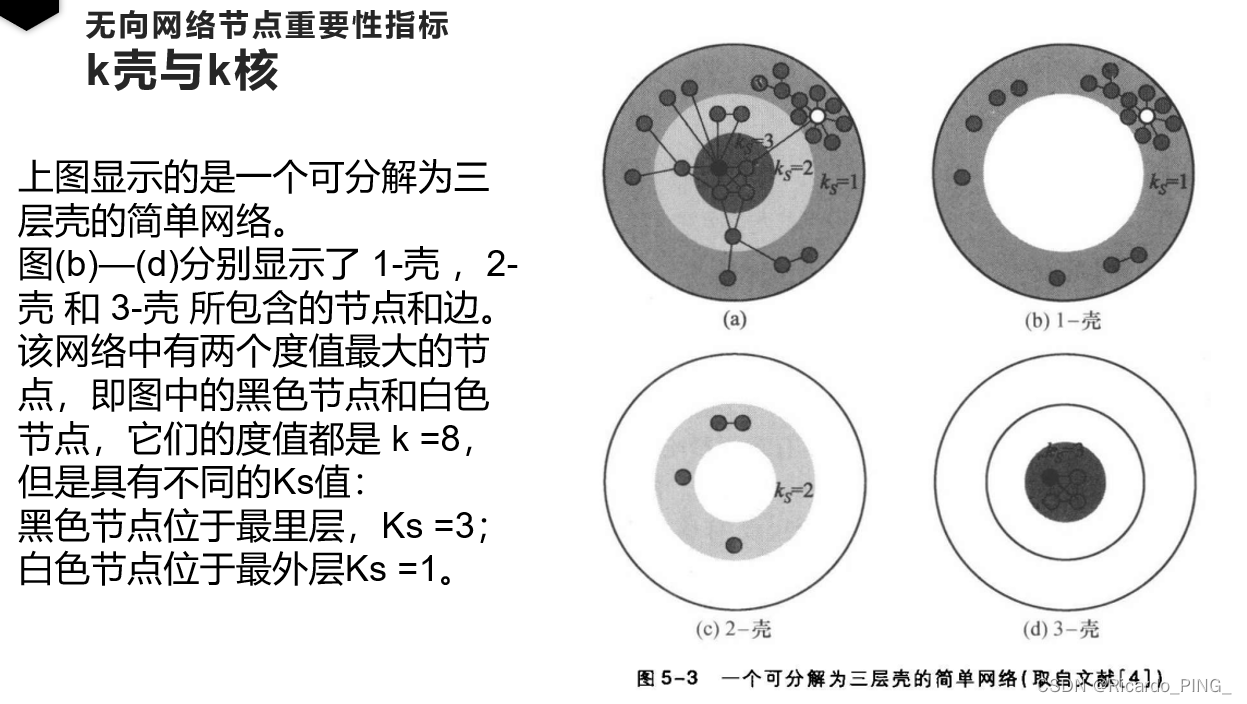
实际网络也会出现类似的情形：

度大的节点既可能具有较大的Ks值从而位于 k-壳分解的核心内层，也有可能具有较小的Ks值而位于k-壳分解的外层，从而使得对于某些问题而言，度大的节点未必是重要的节点。

在得到一个网络的 k-壳 分解之后，我们

把所有Ks≥K 的 K-壳 的并集称为网络的k-核(K-core)

把指标Ks≤K 的 K-壳 的并集称为网络的k-皮(K-crust)

k-核的一个等价定义是:

它是一个网络中所有度值不小于 K 的节点组成的连通片。

基于这一定义，我们可以按照如下方法得到k-核:

首先去除网络中度值小于K的所有节点及其连边；如果在剩下的节点中仍然有度值小于K的节点，那么就继续去除这些节点，直至网络中剩下的节点的度值都不小于K。依次取K = 1,2,3，...，对原始网络重复这种去除操作，就得到了该网络的 k-核分解(k-core decomposition)。

 

1.5 特征向量中心性 

特征向量中心性(Eigenvector centrality)的基本想法是:

一个节点的重要性既取决于其邻居节点的数量(即该节点的度)，也取决于其邻居节点的重要性。

换句话说，在一个网络中，如果一个人拥有很多重要的朋友，那么他也将是非常重要的。

特征向量中心性和度中心性不同，一个度中心性高即拥有很多连接的节点，特征向量中心性不一定高，因为所有的连接者有可能特征向量中心性很低。同理，特征向量中心性高并不意味着它的点度中心性高，它拥有很少但很重要的连接者也可以拥有高特征向量中心性。

 

 

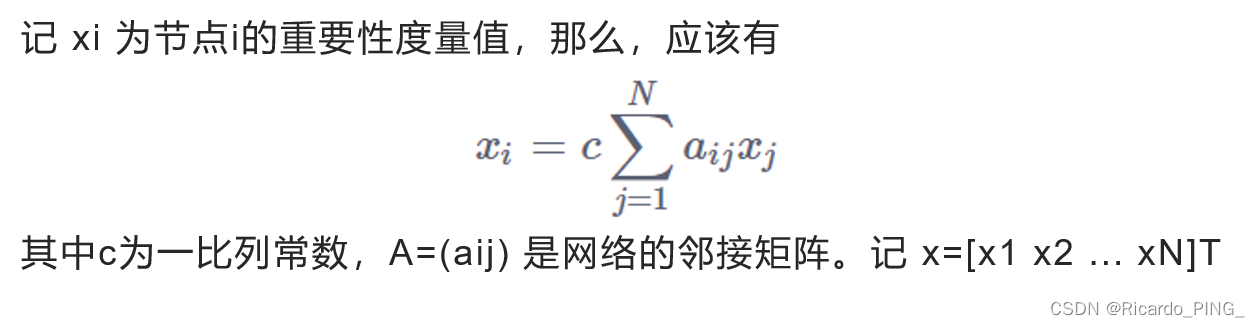
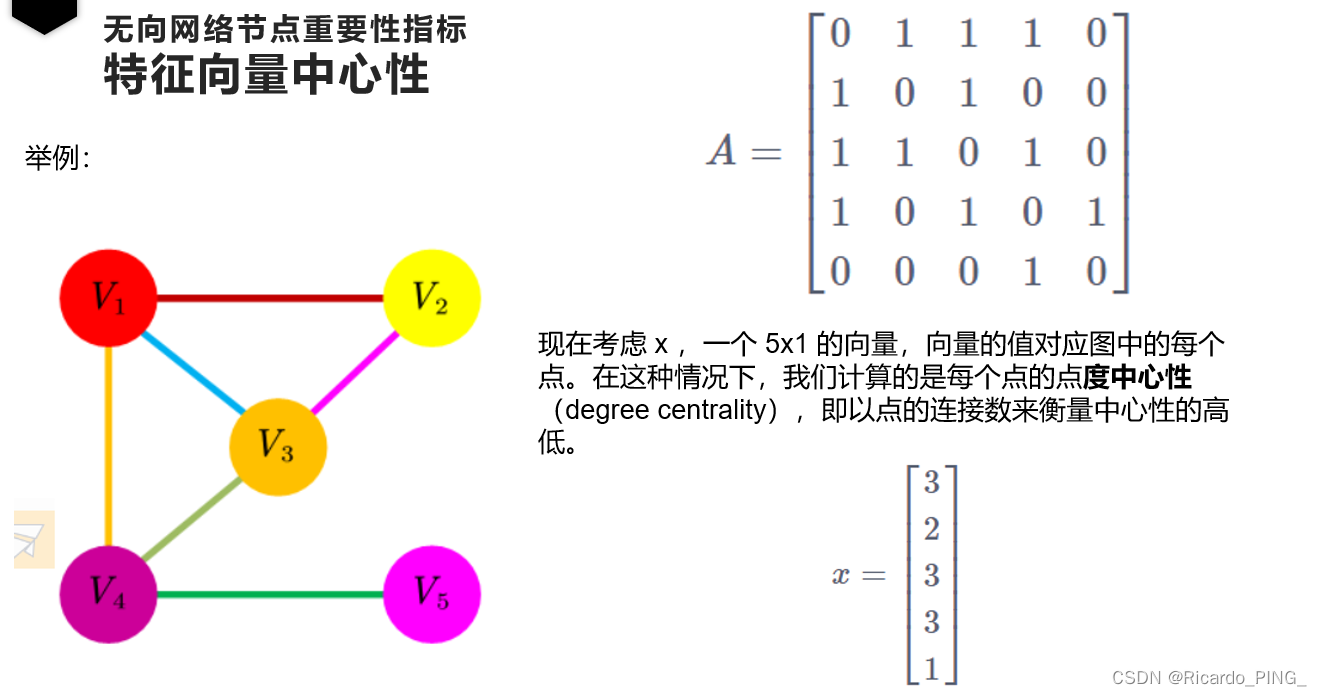
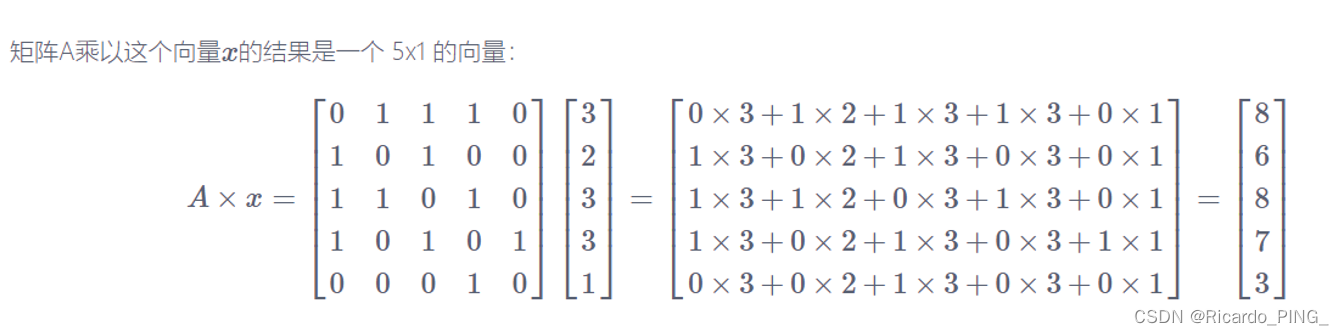
我们继续用矩阵A乘以结果向量。如何理解呢？

实际上，我们允许这一中心性数值再次沿着图的边界“扩散”。我们会观察到两个方向上的扩散（点既给予也收获相邻节点）。我们猜测，这一过程最后会达到一个平衡，特定点收获的数量会和它给予相邻节点的数量取得平衡。既然我们仅仅是累加，数值会越来越大，但我们最终会到达一个点，各个节点在整体中的比例会保持稳定。

※邻接矩阵A是对称矩阵

实对称矩阵的主要性质：

1、实对称矩阵A的不同特征值对应的特征向量是正交的。

2、实对称矩阵A的特征值都是实数，特征向量都是实向量。

3、n阶实对称矩阵A必可相似对角化，且相似对角阵上的元素即为矩阵本身特征值。

4、若λ0具有k重特征值　必有k个线性无关的特征向量，或者说必有秩r(λ0E-A)=n-k，其中E为单位矩阵。

 

2 权威值和枢纽值：HITS算法 

 2.1 HITS算法描述

HITS算法的全称是Hyperlink-Induced Topic Search。在HITS算法中，每个页面被赋予两个属性：hub属性和authority属性。同时，网页被分为两种：hub页面和authority页面。hub，中心的意思，所以hub页面指那些包含了很多指向authority页面的链接的网页，比如国内的一些门户网站；authority页面则指那些包含有实质性内容的网页。HITS算法的目的是：当用户查询时，返回给用户高质量的authority页面。 

很多算法都是建立在一些假设之上的，HITS算法也不例外。HITS算法基于下面两个假设：

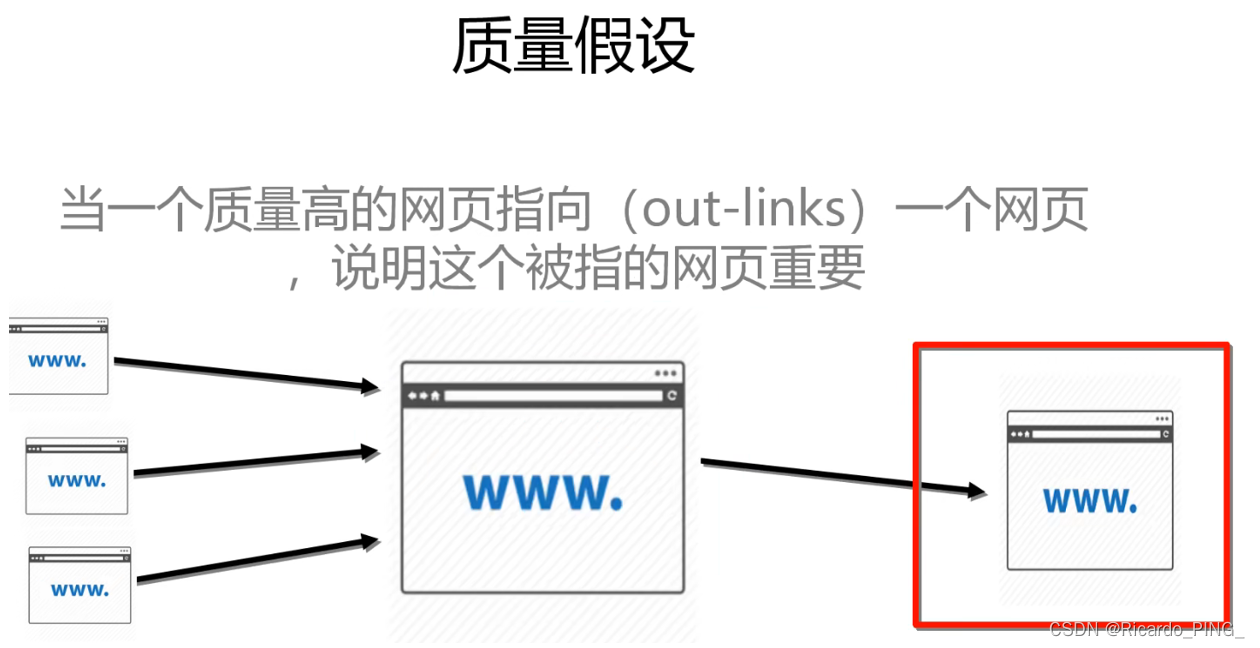
一个高质量的authority页面会被很多高质量的hub页面所指向。

一个高质量的hub页面会指向很多高质量的authority页面。

什么叫“高质量”，这由每个页面的hub值和authority值确定。其确定方法为：

页面hub值等于所有它指向的页面的authority值之和。

页面authority值等于所有指向它的页面的hub值之和。

 

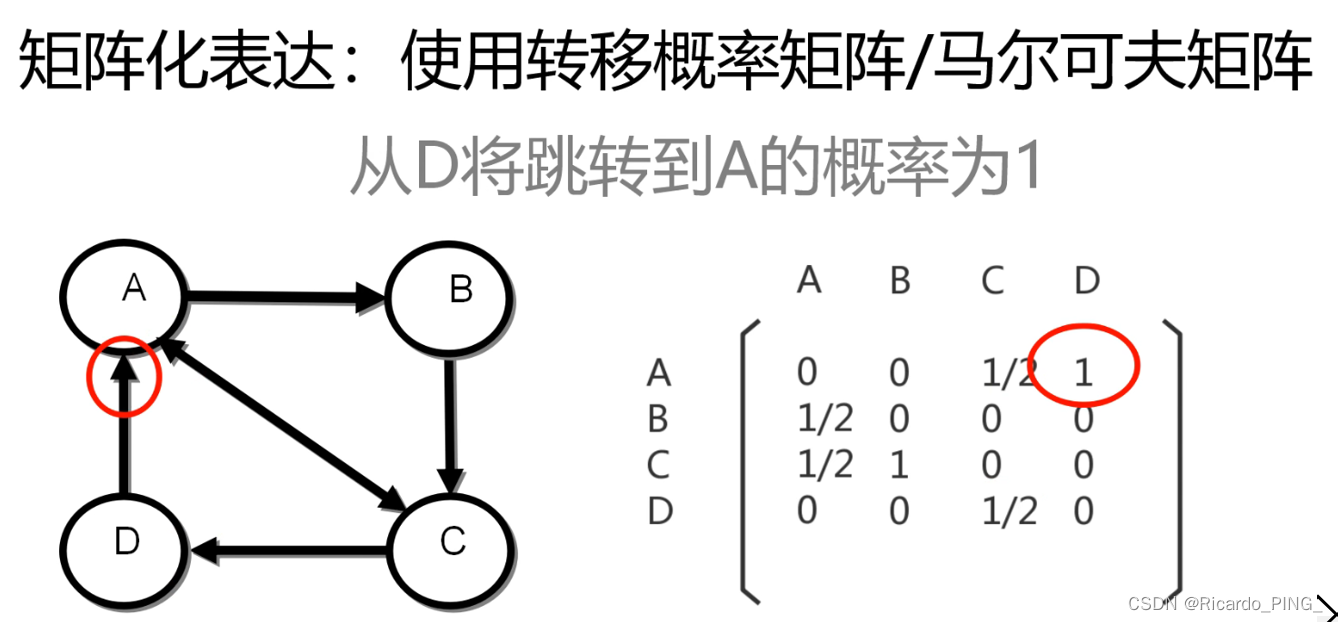
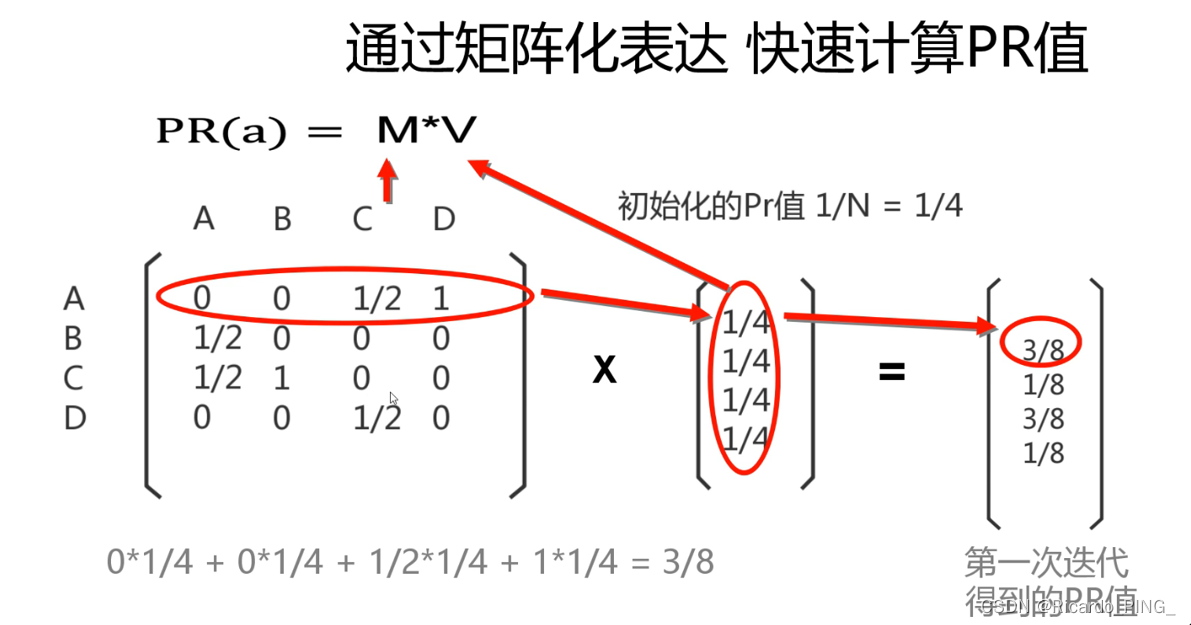
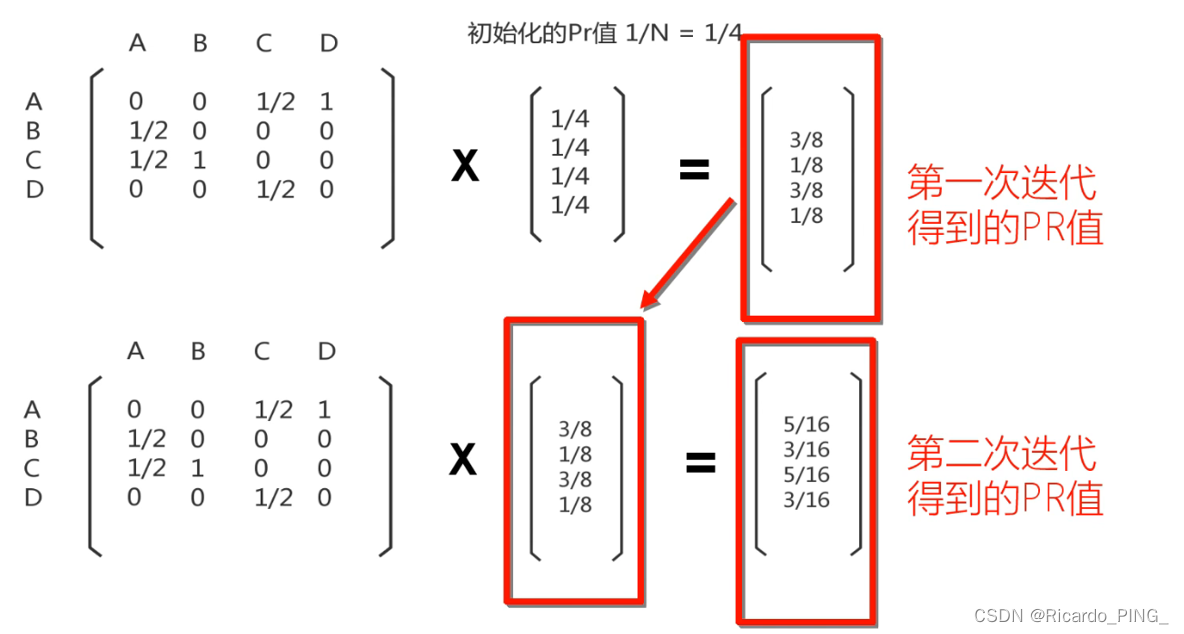
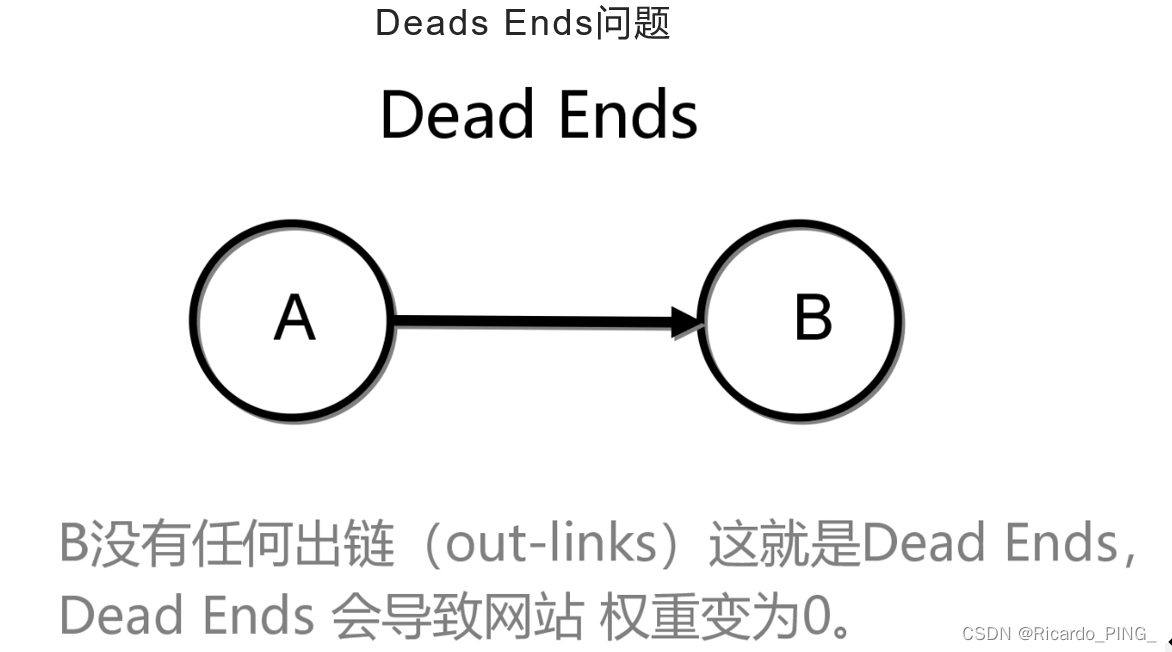
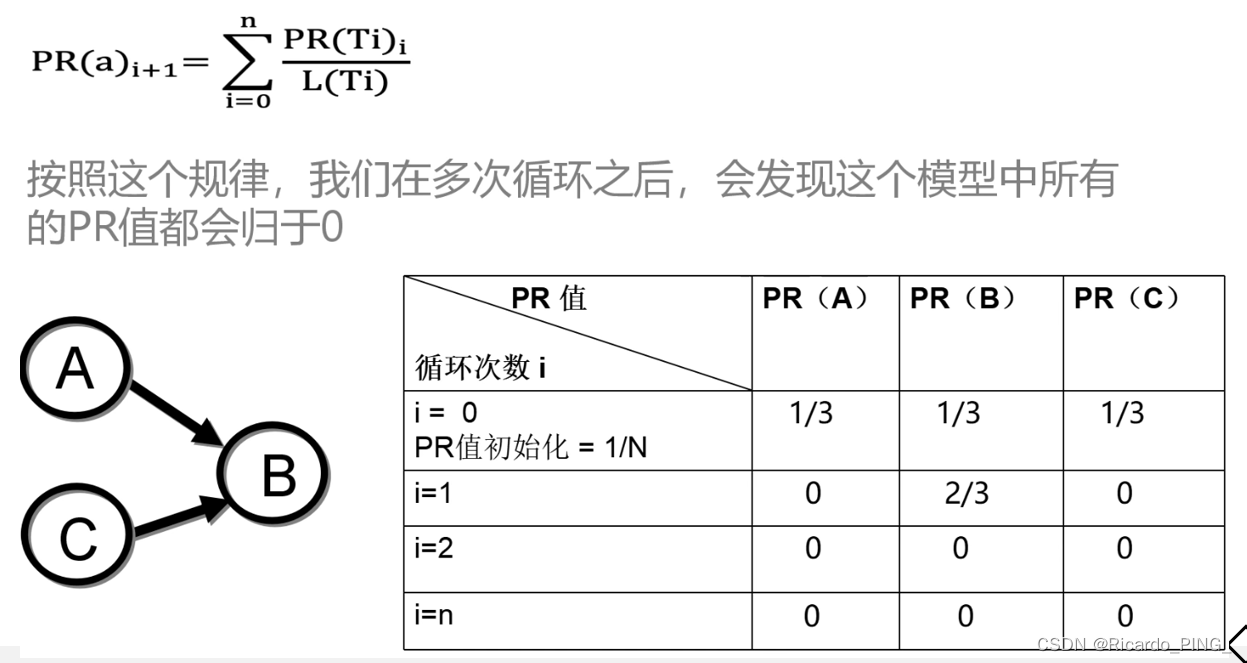
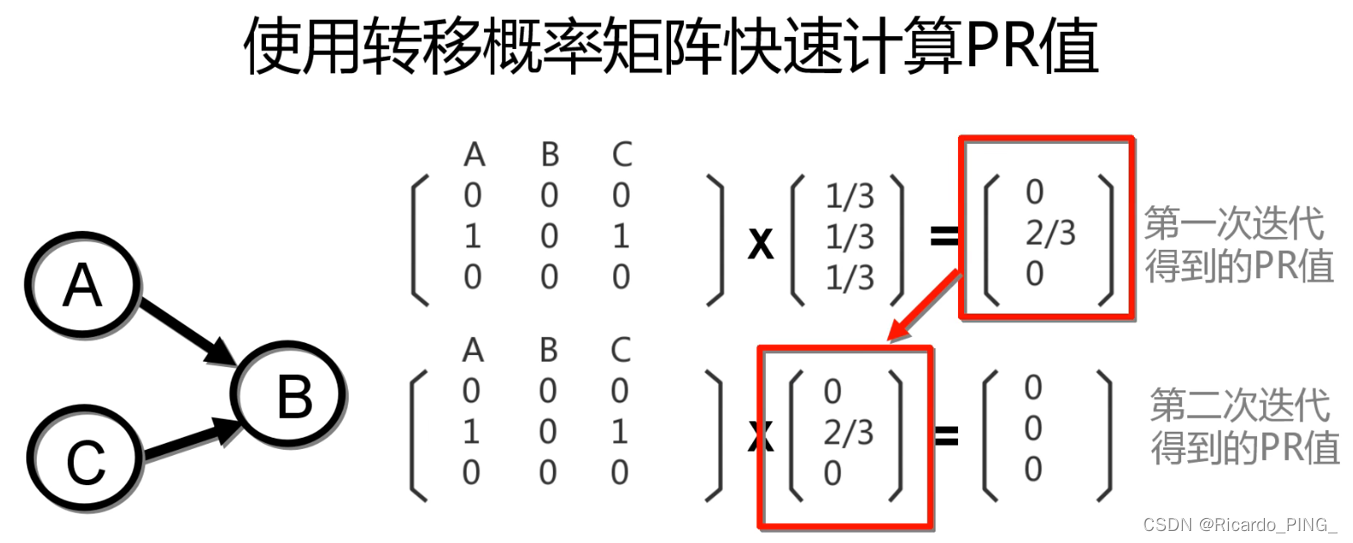
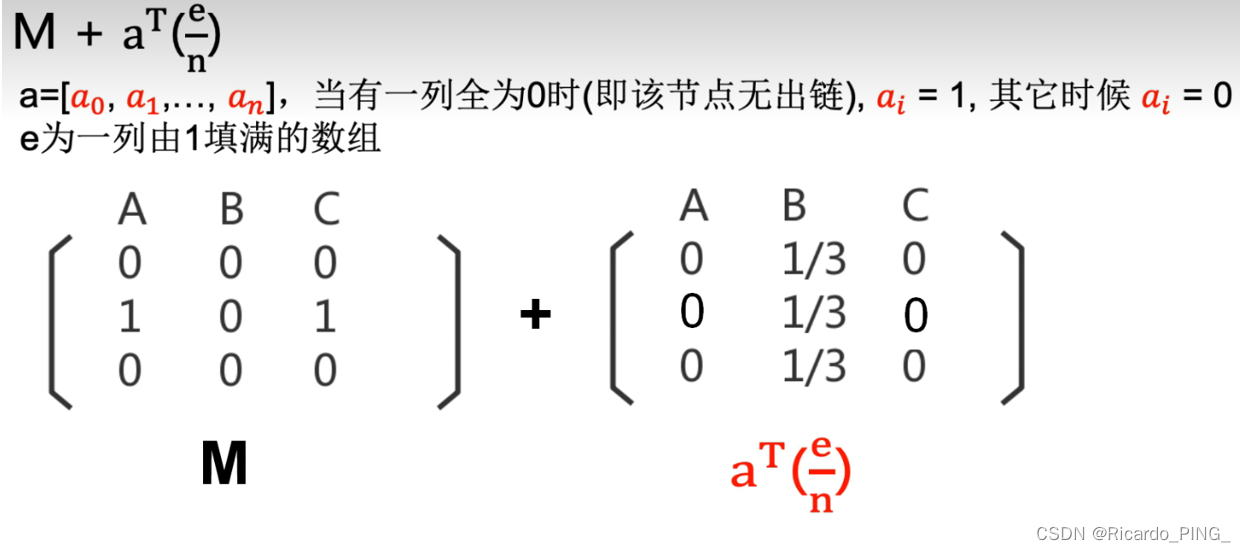
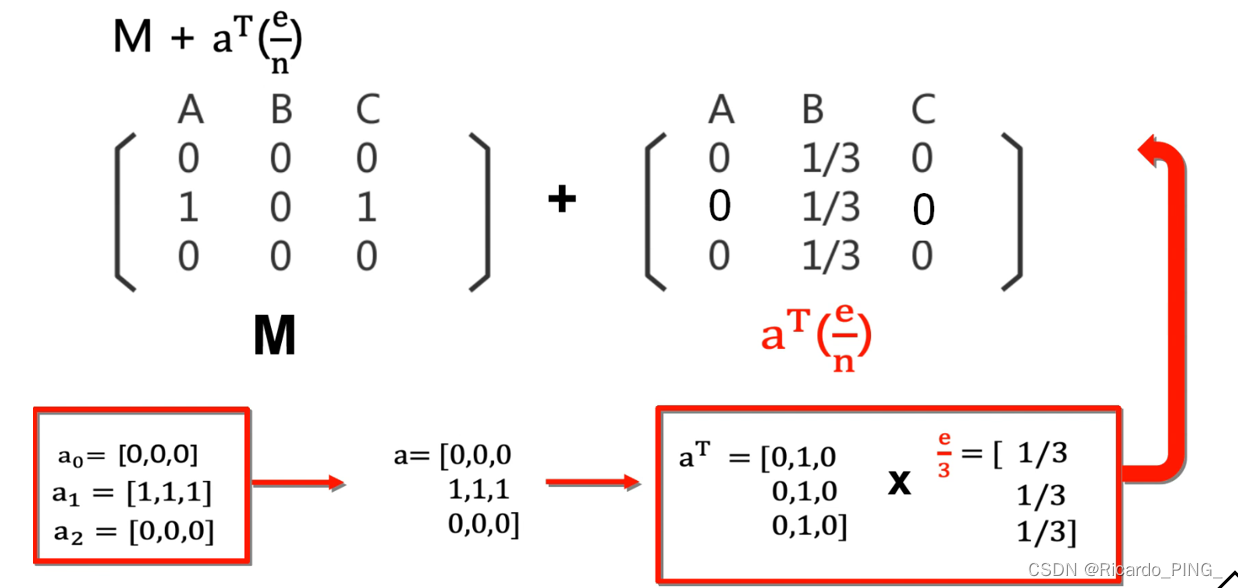
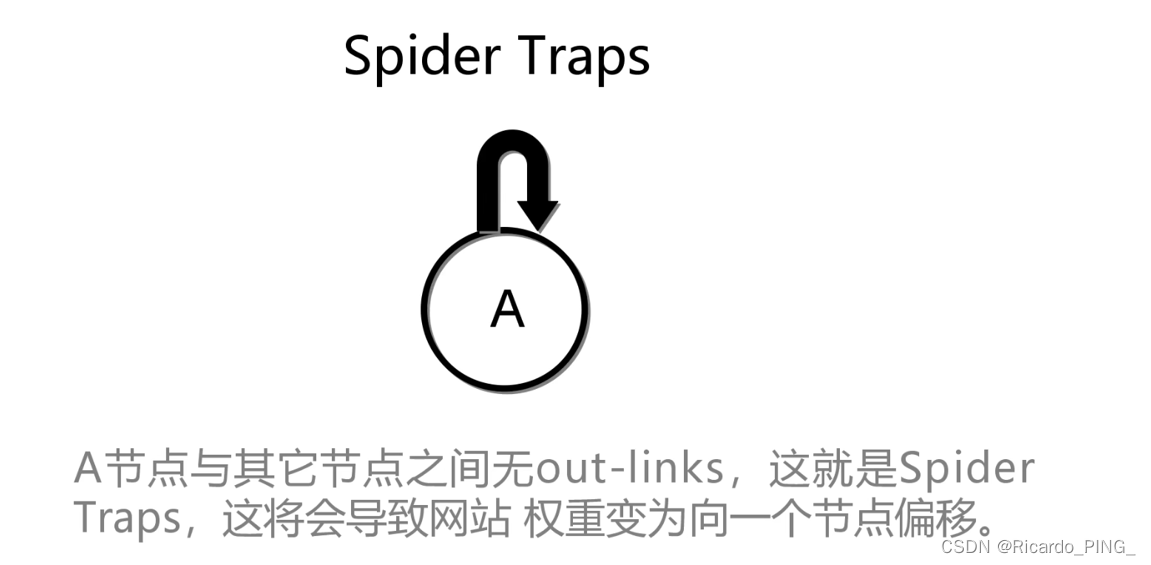
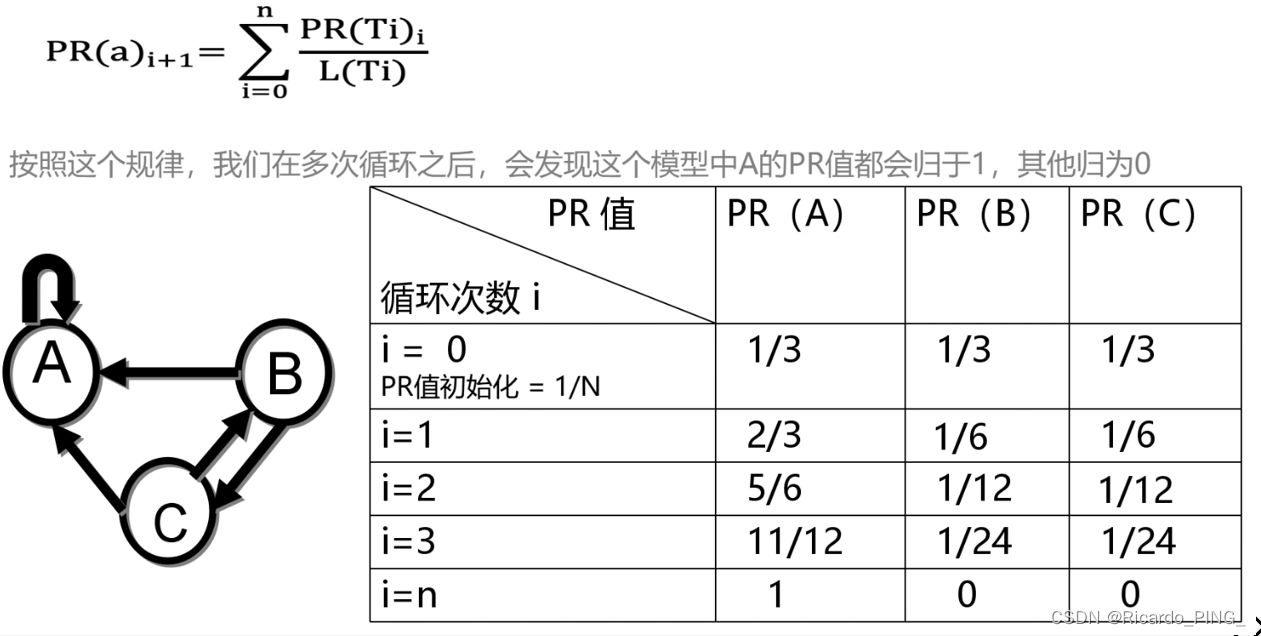
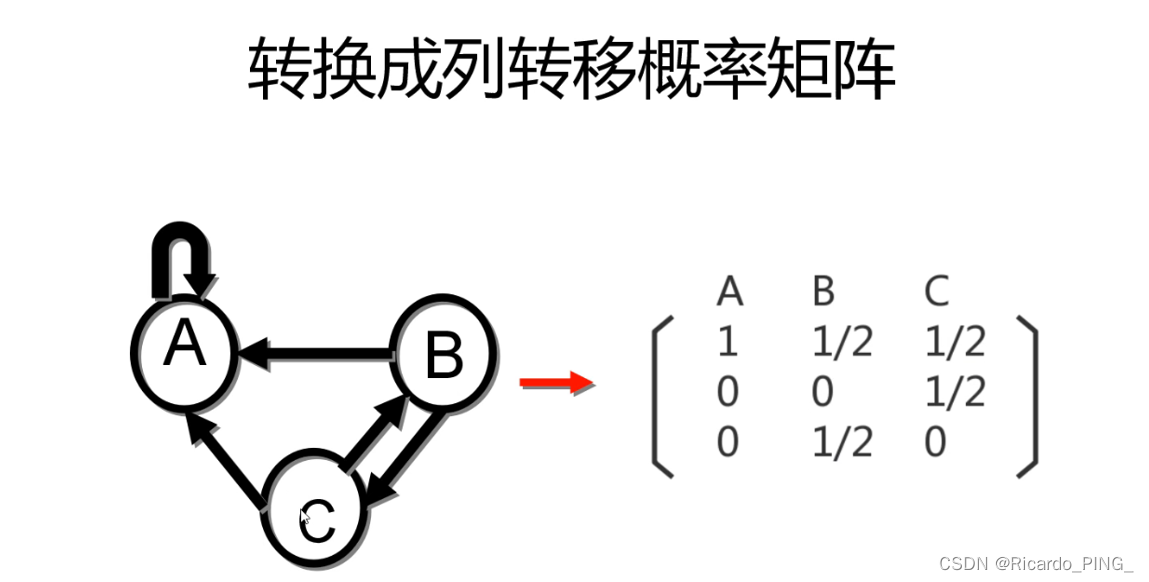
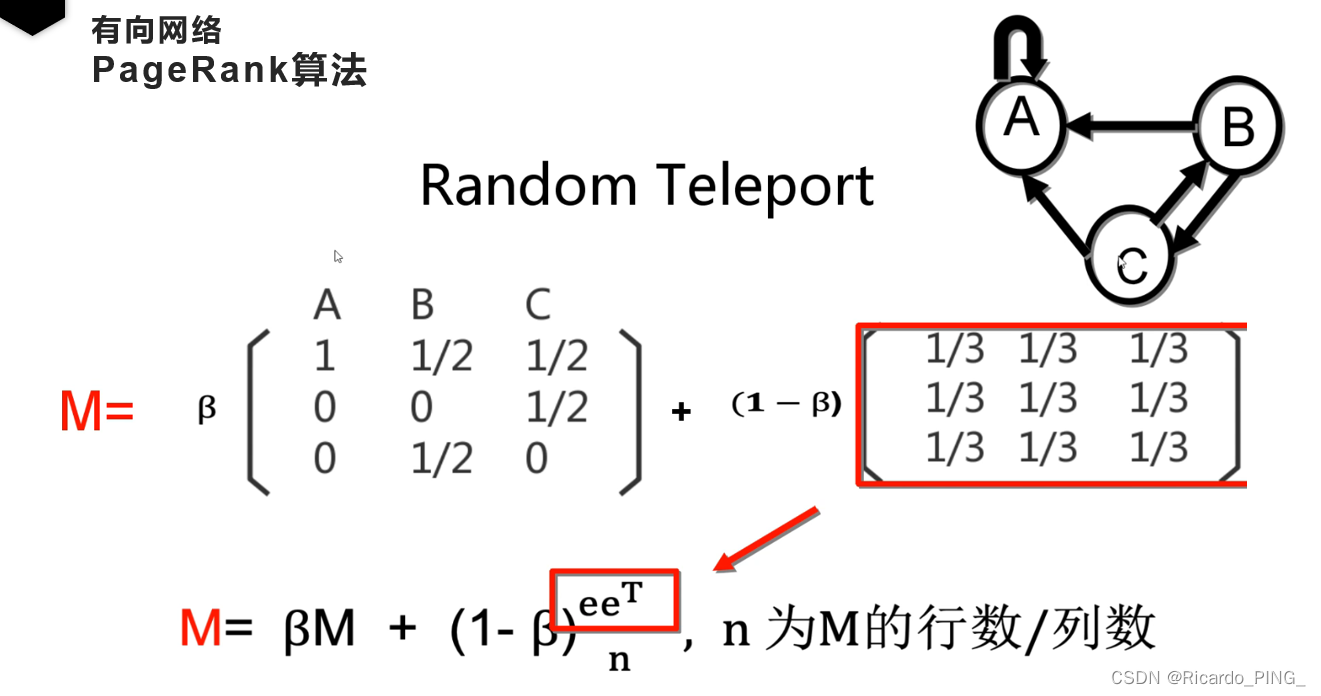
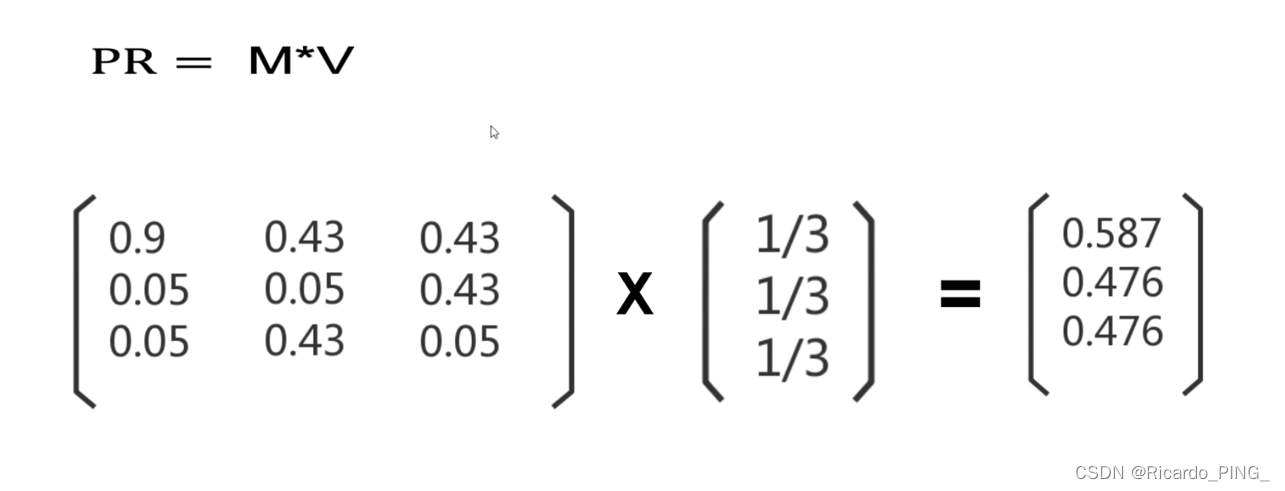
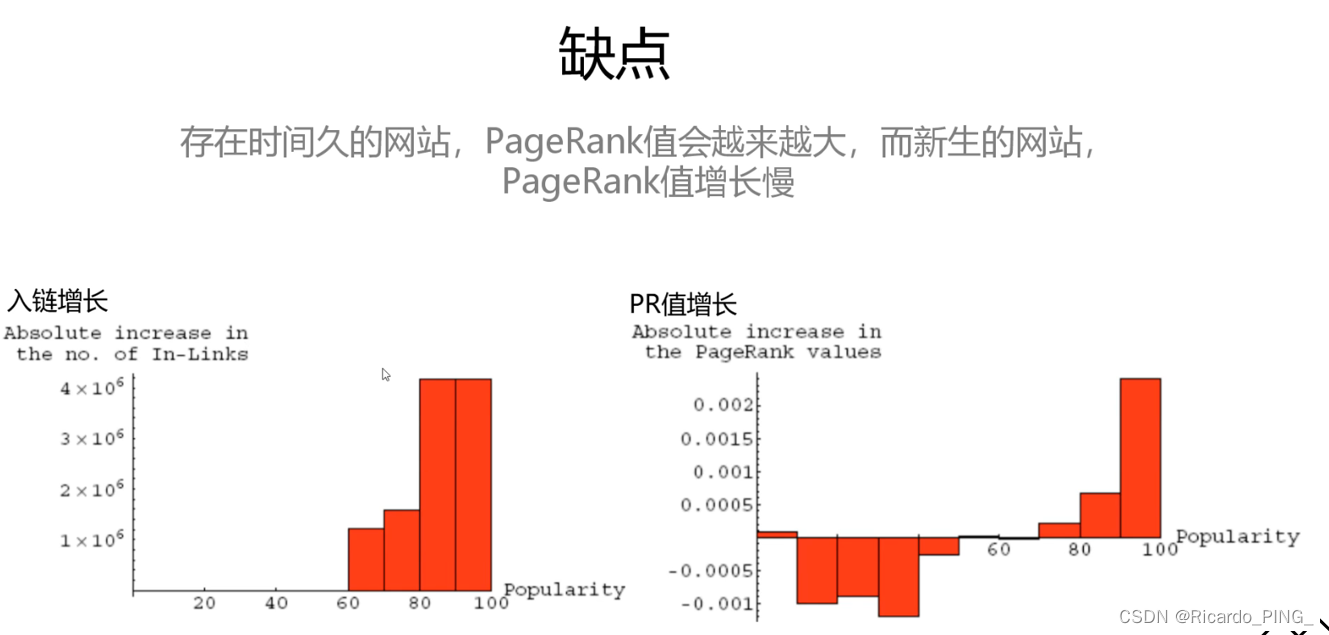
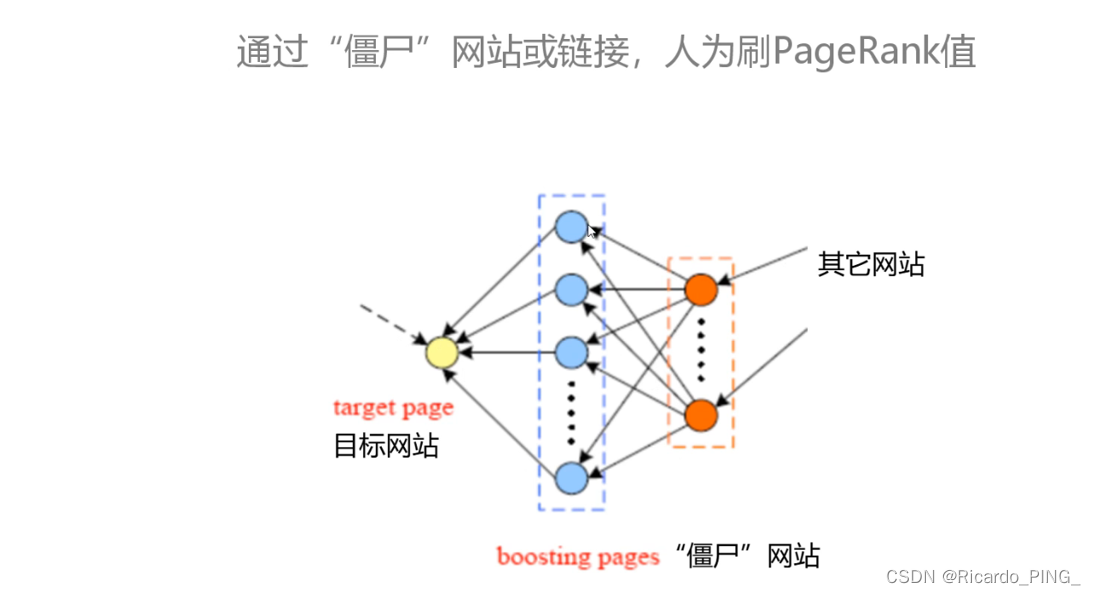
 3 PR值：PageRank算法

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

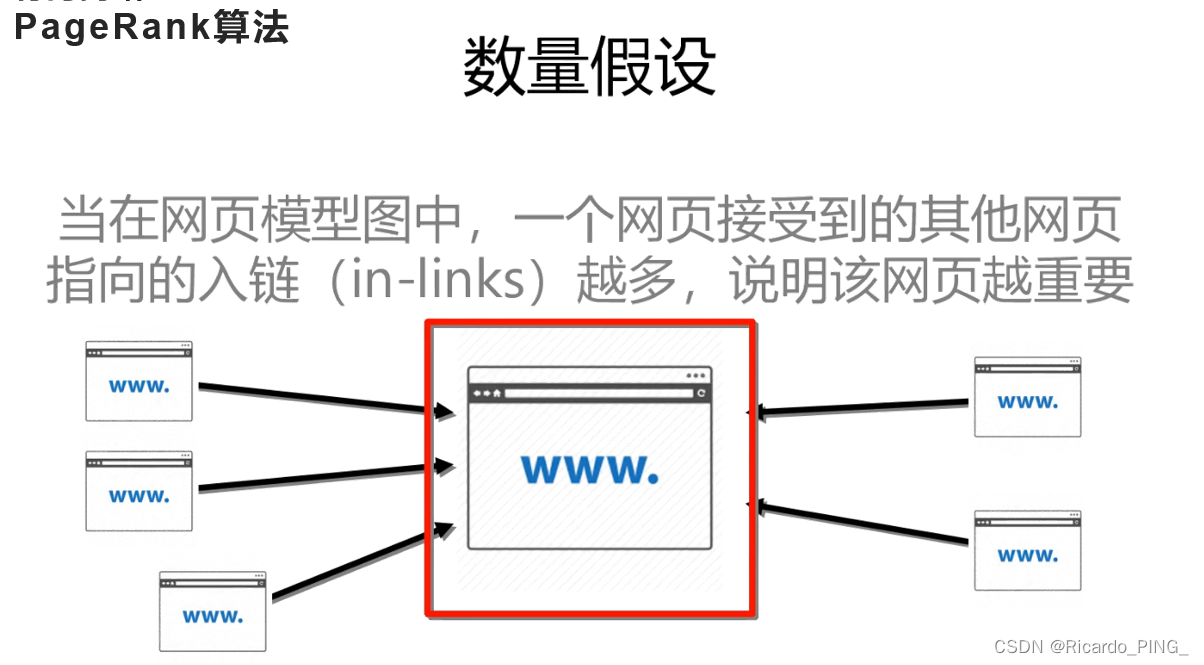
4 节点相似性和链路预测