验证回文串问题带你轻松学会

验证回文串I

1.对应letecode链接

验证回文串I

2.题目描述

3.题目描述

本题非常的简单我们只需首先将字符和数字提起保存到另外一个字符串里面。然后定义一个指针指向开头，一个指针指向结尾然后统一转成小写如果相等继续不相等直接返回false。

4.对应代码

class Solution {
public:
    bool isPalindrome(string s) {
        
          string str;
          for(auto ch:s)
          {
              if(isdigit(ch)||isalpha(ch)){
                     str+=ch;
              }
              //将字符和数字提起收集起来
          }


          int L=0;
          int R=str.size()-1;
          while(L<=R)
          {
              //同一转成小写
              if(tolower(str[L])==tolower(str[R])){
                 L++;
                 R--;
              }else{
                   return false;
              }
          }
          return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

非常的简单。

验证回文串II

1.对应letecode链接
验证回文串II
2.题目描述

3.解题思路

本题思路还是很简单的，首先一样的我们定义一个指针指向字符串的开头位置定义一个指针指向字符串的结尾位置。一起向中间遍历如果相等就继续走不相等可以尝试把L位置的字符抛弃掉或者尝试把R位置的字符抛弃掉。然后在看看剩下的字符是不是这个回文串如果是则返回true不是直接返回false即可。

4.对应代码

class Solution {
public:
    bool validPalindrome(string s) {
        int L=0;
        int R=s.size()-1;
        bool ans=true;
        while(L<R)
        {
           if(s[L]==s[R]){
               L++;
               R--;
           }else{
               //给他一次机会
                ans= CheckPalindrome(s,  L+1, R)||CheckPalindrome(s,  L, R-1);
                break;
           }
        }
        return ans;
    }

    //判断[L.....R]范围内是否是回文串
    bool CheckPalindrome(const string&str,int L,int R)
    {
              while(L<R)
              {
                  if(str[L]!=str[R]){
                       return false;
                  }
                  L++;
                  R--;
              }
              return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

验证回文串III

1.对应letecode链接
验证回文串III
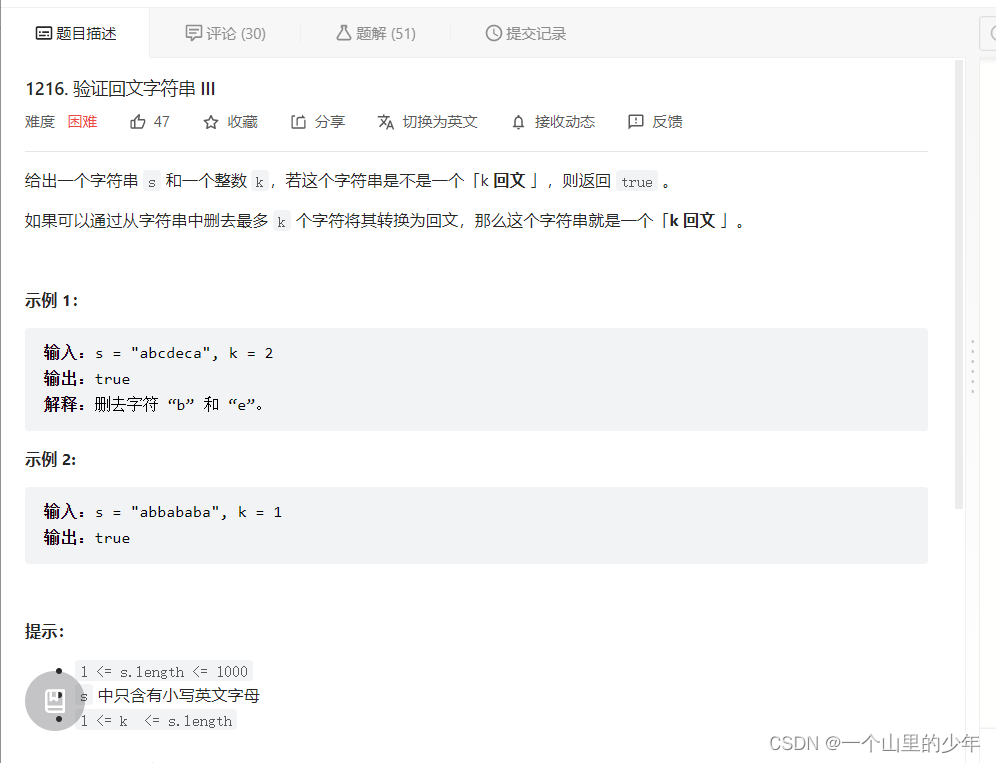
2.题目描述

3.解题思路

本题相比较上题难度大了不少，本题的解题思路就是既然是最多删除k个字符。那么我们就要想了，如果我们求出这个字符串的最长回文子序列，此时这个字符串想要变成回文串就必须把最长回文子序列之外的字符给删除掉。因此我们只需要求出字符串最长回文子序列然后用字符串的长度减去最长回文子序列看看这个值是不是小于等于k即可。那么下面的任务就是怎么求最长回文子序列的问题了。最长回文子序列是典型的范围尝试模型。从L到R范围内的尝试模型。下面我们分析一下可能性：
可能性1：最长回文子序列可能以R结尾但是不以L开头
可能性2:最长回文子序列可能以L开头但是不以R结尾
可能性3：最长回文子序列既以L开头又以R结尾此时必须要L位置的字符要和R位置的字符相等。
可能性4：可能性四可以忽略他一定没有可能性1和可能性2长。

4.对应代码

class Solution {
public:
    vector<vector<int>>dp;
    bool isValidPalindrome(string s, int k) {
        int N=s.size();
        dp.resize(N,vector<int>(N+1,-1));
          int maxLen=process(s,0,s.size()-1);
       
          return (s.size()-maxLen)<=k;
    }
    //(L....R)范围内最长回文子序列的长度
    int process(const string&str,int L,int R){
               if(L==R){
                   return 1;
               }
               //只有两个字符了
               if(L==R-1){
                   return str[L]==str[R]?2:1;
               }
               if(dp[L][R]!=-1){
                   return dp[L][R];
               }

               int p1=process(str,L+1,R);
               //一定不以L位置开头但是可以以R位置结尾
               int p2=process(str,L,R-1);
               int ans=max(p1,p2);
               //开头位置的字符和结尾位置字符相等
               if(str[L]==str[R]){
                   ans=max(ans,2+process(str,L+1,R-1));
               }
               dp[L][R]=ans;
               return ans;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

对应严格位置依赖的动态规划

class Solution {
public:
    
    bool isValidPalindrome(string s, int k) {
      
         int N=s.size();
         vector<vector<int>>dp(N,vector<int>(N));
         dp[N-1][N-1]=1;  
         for(int i=0;i<N-1;i++)
         {
             dp[i][i]=1;
             dp[i][i+1]=(s[i]==s[i+1]?2:1);
         }

         for(int L=N-3;L>=0;L--)
         {
             for(int R=L+2;R<N;R++)
             {
                 if(s[L]==s[R])
                 {
                    dp[L][R]=dp[L+1][R-1]+2;
                 }
                 else
                 {
                     dp[L][R]=max(dp[L][R],max(dp[L+1][R],dp[L][R-1]));
                 }
             }

         }
         return (N-dp[0][N-1])<=k;
       
    }
 
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34