字符串——实现 strStr()——KMP

28. 实现 strStr()——KMP算法

重点总结

1. 要在haystack字符串：aabaabaaf 中查找是否出现过一个 needle 字符串：aabaaf
2. 前缀表是从needle 字符串中找规律 。不关haystack 字符串的事
3. 前后缀相等不是找对称，不要被例子的aa误导，以为是对称。如abcab，前后缀都是从前往后，最长前后缀相等应该是ab，不是对称
4. 前缀表作用：记录部分匹配的地址，不用重新匹配

题目

力扣链接
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

提示：

1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成

思路

暴力解法

第一个for循环遍历haystack 字符串
第二个for循环匹配needle 字符串找相同

class Solution {
public:
    int strStr(string haystack, string needle) {
        for(int i=0;i<haystack.size();i++)
        {
            for(int j=0;j<needle.size();j++)
            {
                if(haystack[i+j]!=needle[j])
                    break;
                else
                    if(j==needle.size()-1)
                    return i;
            }
        }
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

KMP 经典算法

思路：从i开始匹配，当字符串不匹配时，而是记录之前已经匹配的部分，从匹配的部分开始。

说明：在上文暴力解法中第一个for循环从i开始遍历haystack 字符串，第二个for开始匹配，匹配到第j个词对不上，后面第二个for结束，(KMP从这里改进)第一个for从i+1开始，后面j从0开始匹配。

算法改进处：KMP通过next数组记录已经匹配的地址（，不从i+1重新开始，而是从i+j部分开始匹配，j读取next数组（前缀表（prefix table））中记录的地址（needle 字符串匹配的位置），再次重新匹配。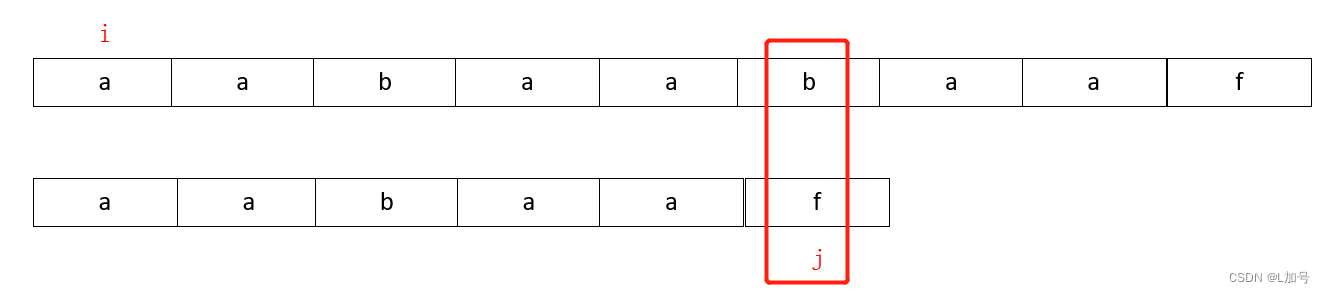

第二次匹配

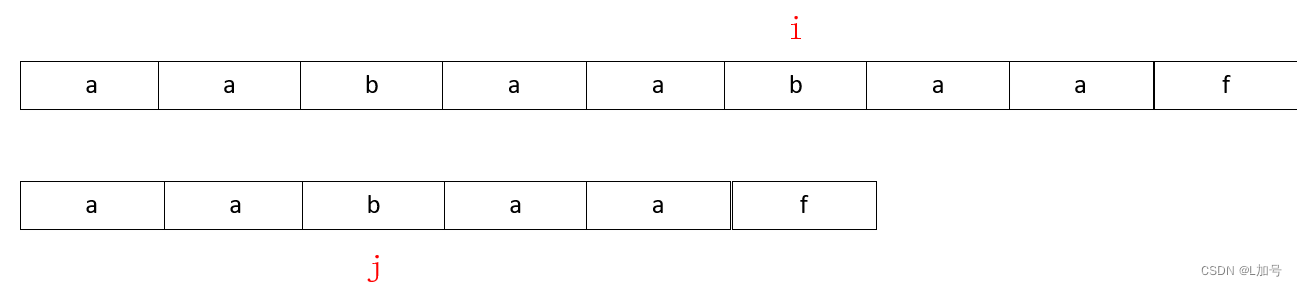
j的位置从前缀表（prefix table）中读取

前缀表（prefix table）

前缀表（prefix table）用next数组表示
前缀表是用来回退的，它记录了needle 字符串与haystack 字符串不匹配的时候，模式串应该从哪里开始重新匹配。

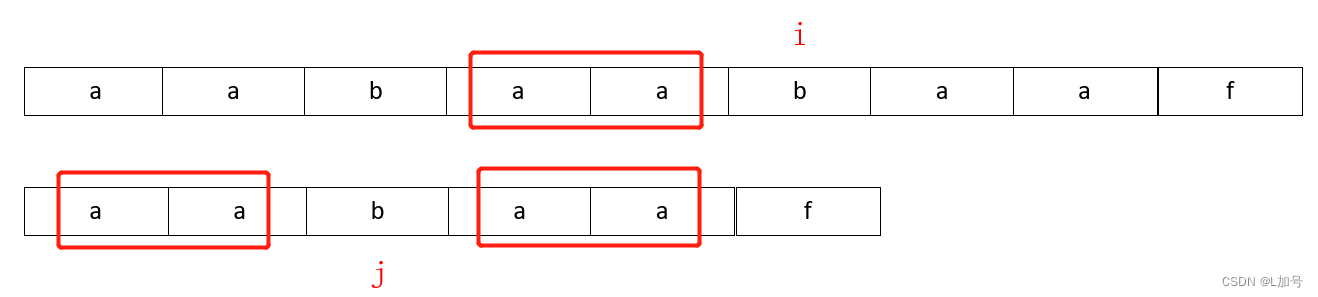
haystack 字符串就第五个（从0开始）不匹配，暴力解法就是haystack 字符串从第一个开始，重新匹配。
但KMP算法就不，他从needle 字符串找规律，找到aa这个特殊的两个连续字符，aa是needle字符串首字符开始的，后面也找的到aa，当后面aa可以匹配，但aa后面第五个字符对不上，要重新匹配，但第三位的a，第四位的a对的上；一看第零位的a、第一位的a，两者不是一样的吗，这next[i]的位置记录的就是2，则j跳到next[2]处。

这样的想法实现就要通过最长公共前后缀

最长公共前后缀

前缀：从首字符开始，不包括最后一个字符的所有子串
后缀：从尾字符开始，不包括开头一个字符的所有子串

例子：是needle字符串（不管haystack 字符串的事）后缀（顺序还是从前开始）
f
af
aaf
baaf
abaaf
前缀
a
aa
aab
aaba
aabaa

公共——指的是前缀和后缀相等的最长长度（比较相等的前后缀长度要相等）

例子：
a——没有前后缀——0
aa——前缀a、后缀a——1
aaa——前缀a、后缀a——1、前缀aa、后缀aa——2，取最大值——2
。。。
最后的值就是j在next数组的位置

为什么叫前缀表——因为第一个for是从前向后匹配，部分相同肯定只有前面部分相同才有用，如果for是从后向前，那就叫后缀表

计算前缀表

总思路
从小到大取前缀表
每个前缀表中比较前后缀，找最长相等前后缀表的值（这个值就是相等的长度）
有两步的
前缀表：先取前缀表，后从前缀表中找最长相等前后缀表

需要的参数：
needle字符串，前缀表（next数组）不管haystack 字符串的事
如图

1. 第一个前缀表
   

无前后缀——0
2. 第二个前缀表

前缀a、后缀a——1
3. 第三个前缀表

前缀a、后缀b——0；前缀aa、后缀ba——0。——0
4. 第四个前缀表

前缀a、后缀a——1；前缀aa、后缀ba——0、前缀aab、后缀aba——0
最大值——1
5. 第五个前缀表

前缀a、后缀a——1；前缀aa、后缀aa——2、前缀aab、后缀baa——0、前缀aaba、后缀abaa——0
最大值——2
前后缀都是从前向后读的，不要被aa误导以为是对称
如abcab
前缀
a
ab
abc
abca
后缀
b
ab
cab
bcab
不是对称也有最长前后缀相等值

前缀表的作用

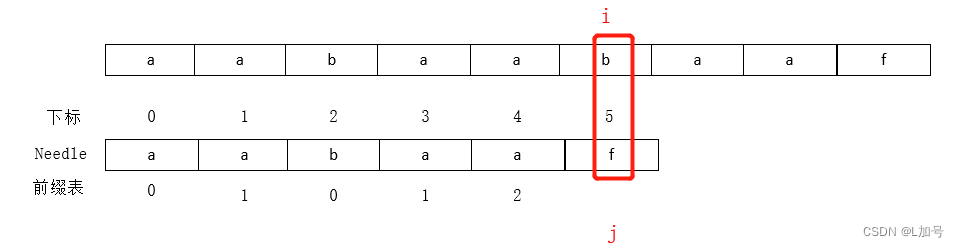
第5位不匹配，查看前缀表前一位的值为2，j跳到下标为2的地方
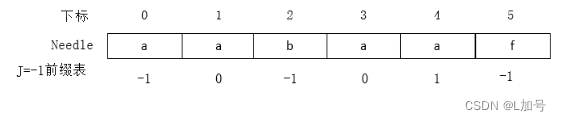
移位的原因（就是第四位的值，这就是为什么有的前缀表右移一位首位加-1，右移一位就不用看前一位的值；前缀表是不包含最后一个字符的，而第一个字符前一个没有，按照实际意义，第一个字符前一个应该表示为结束，所以添-1）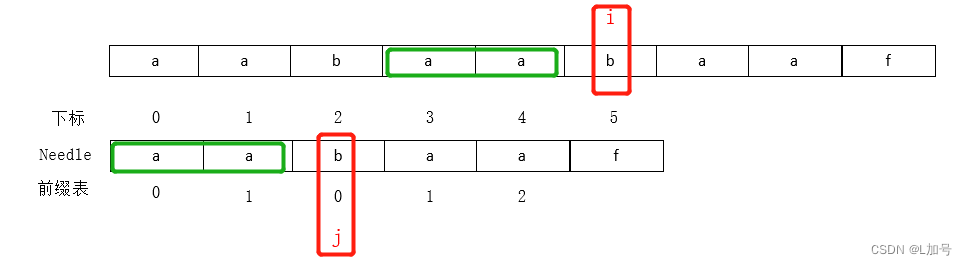

绿色部分为记录的部分相同值（aa就是部分相同的）
红色部分为要比较
前缀表作用：记录部分匹配的地址，不用重新匹配

next数组（前缀表）

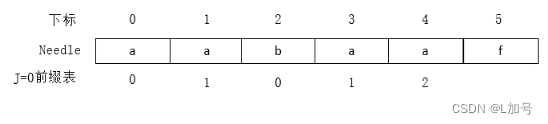
用next数组表示前缀表
本次例子使用不移位的前缀表（移位原因在上文标黄处）
如图：

前缀表数值上文例子中说明了

构造next数组

定义一个函数

    void getNext(int* next,const string& s)
1

next为构建的数组
s只需要needle字符串，前缀表是什么，就是从needle字符串中找到的规律
函数有2步
第一步——初始化
第二步——处理前后缀比较的结果

初始化

本文使用不移位，不减一（移位、减一不关KMP算法的思路，就是循环中位置不一样罢了，后文会举例）
设置两个指针（指向地址为什么是这些，后文会说）
i指向后缀的末尾
j指向前缀的开头
比较前后缀相等从短到长的比较
如：abcab（不用aabaaf，让人有对称的想法，这是错的，我一开始以为对称，怎么想怎么不对）
如后缀cab，i指向末尾b
前缀abc，j指向开头a
读取是按照从前向后，前缀：第零位和第一位：ab；后缀：第三位和第四位：ab，有相等，不是对称

        int j=0;
        next[0]=j;
1
2

处理前后缀比较的结果

第一步：遍历haystack 字符串

for(int i=1;i<s.size();i++)
1

i=0的位置已经初始化为0，所以从1开始

前文写到
前缀表总思路
从小到大取前缀表
每个前缀表中比较前后缀，找最长相等前后缀表的值（这个值就是相等的长度）

这个for循环执行——从小到大取前缀表
每个前缀都可以看作匹配成功的部分
如i=1时，表示的为前缀为字符0位、字符1位匹配成功，字符2位不匹配的情况
如i=2时，表示的为前缀为字符0位到字符2位匹配成功，字符3位不匹配的情况
for循环中的i表示i+1位不匹配的情况

前后缀不等的情况

            while(j>0 && s[i]!=s[j]){//不等情况
                j=next[j-1];
            }
            if(s[i]==s[j]) //相等情况
                j++;
            next[i]=j;
1
2
3
4
5
6

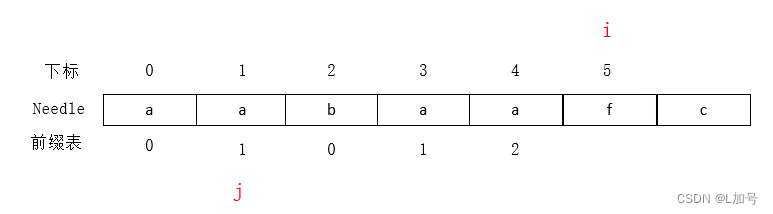
1. 第一次比较特殊：j初始为0，i初始为1，刚好前缀就两位，可以比较
   
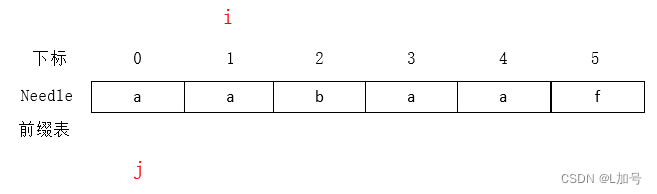
   next[1]不等就存0，相等就j++，存1
   
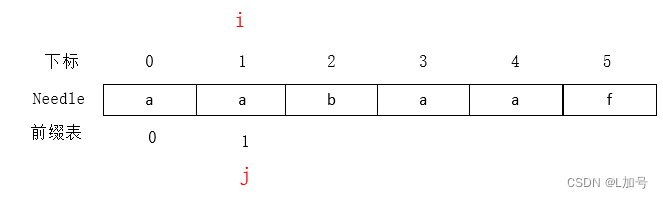
2. j为1，i为2，为什么j为1，不是0呢
   
   因为前缀表一步一步增加一个字符是有规律的

aaba 的前缀a、后缀a——前缀表值为1
aabaa的前缀aa、后缀aa——前缀表值为2

前缀表字符个数为n时，如果前缀表值为m时
前缀表字符个数为n+1时，前缀表值为m+1或则为小于m值
（n的前后缀匹配个数为m，n+1比n就长一，这个一要不使匹配数多一，要不使匹配的开始端变位置）
（可以自己举例子试一试）

            while(j>0 && s[i]!=s[j]){//不等情况
                j=next[j-1];//回退
            }
1
2
3

j>0表示为匹配的长度不小于0，等于0说明没有匹配的，不用回退了，退无可退
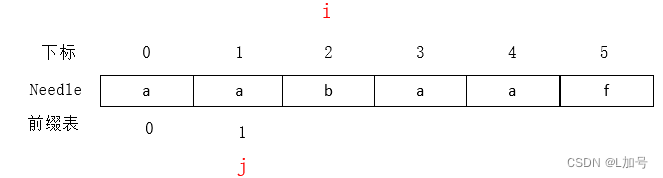
如图中

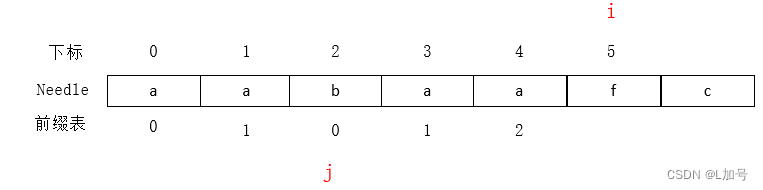
            while(j>0 && s[i]!=s[j]){//不等情况
                j=next[j-1];//回退
            }
1
2
3

i和j指向不相等，要回退一步

j指向1，实际意义：j=2时，第二位对不上，前面部分对的上，中间对不上，那前面部分对的上也没用了，拿最长匹配的部分比对，对的上就重新设置，对不上就拿最长匹配的部分回退到上一状态（匹配的部分只能一步一步+1），直到j=0，说明都对不上，这个前缀没有前后缀相等的next[i]=0，然后可以i+1了
2. 相等情况

            if(s[i]==s[j]) 
                j++;
            next[i]=j;
1
2
3

前文说了，i的每次变化，j增加只可能+1
j的变化只可能在[0,j+1]

整体代码

    void getNext(int* next,const string& s)
    {
        int j=0;
        next[0]=j;
        for(int i=1;i<s.size();i++)
        {
            while(j>0 && s[i]!=s[j]){
                j=next[j-1];
            }
            if(s[i]==s[j]) 
                j++;
            next[i]=j;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

使用next数组来做匹配

使用就简单
i遍历haystack字符串

for(int i=0;i<haystack.size();i++)
1

j遍历needle字符串

        int j=0;
        for(int i=0;i<haystack.size();i++)
        {
            while(j>0 && haystack[i]!=needle[j])//不等的情况下，j回退到部分匹配的坐标
            {
                j=next[j-1];
            }
            if(haystack[i]==needle[j]){//相等就是再比较下一个
                j++;
            }
            if(j==needle.size()){//j到了needle的末尾，说明都对上了
                return (i-needle.size()+1);
            }
        }
        return -1;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

代码中就是i遍历haystack字符串，j遍历needle字符串，
对的上就j++，i++，比较下一位
对不上就 j=next[j-1];使用计算好的前缀表，跳到部分匹配的部分

整体代码j=0

//j=0
class Solution {
public:
    void getNext(int* next,const string& s)
    {
        int j=0;
        next[0]=j;
        for(int i=1;i<s.size();i++)
        {
            while(j>0 && s[i]!=s[j]){
                j=next[j-1];
            }
            if(s[i]==s[j]) 
                j++;
                next[i]=j;
        }
    }
    int strStr(string haystack, string needle) {
        if(needle.size()==0){
            return 0;
        }
        int next[needle.size()];
        getNext(next,needle);
        int j=0;
        for(int i=0;i<haystack.size();i++)
        {
            while(j>0 && haystack[i]!=needle[j])
            {
                j=next[j-1];
            }
            if(haystack[i]==needle[j]){
                j++;
            }
            if(j==needle.size()){
                return (i-needle.size()+1);
            }
        }
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

j=-1的情况比较

//j=-1
class Solution {
public:
    void getNext(int* next,const string& s)
    {
        int j=-1;
      	//int j=0;
        next[0]=j;
        for(int i=1;i<s.size();i++)
        {
            while(j>=0 && s[i]!=s[j+1]){  //while(j>0 && s[i]!=s[j]){   大于等于变成大于
                j=next[j]; //j=next[j-1]; j=-1比j=0右移一位
            }
            if(s[i]==s[j+1]) //if(s[i]==s[j])。从-1开始，所以j+1
                j++;
                next[i]=j;
        }       
    int strStr(string haystack, string needle) {
        if(needle.size()==0){
            return 0;
        }
        int next[needle.size()];
        getNext(next,needle);
        int j=-1;
        //int j=0;
        for(int i=0;i<haystack.size();i++)
        {
            while(j>=0 && haystack[i]!=needle[j+1])//while(j>0 && haystack[i]!=needle[j])
            {
                j=next[j];//j=next[j-1];
            }
            if(haystack[i]==needle[j+1]){//if(haystack[i]==needle[j]){
                j++;
            }
            if(j+1==needle.size()){
                return (i-needle.size()+1);
            }
        }
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

j=0或j=-1，只是j的位置发生变化，不影响KMP算法