-
洛谷 P3376 【模板】网络最大流
PS:如果读过题了可以跳过题目描述直接到题解部分
提交链接:洛谷 P3376 【模板】网络最大流题目
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入格式
第一行包含四个正整数 n , m , s , t n,m,s,t n,m,s,t,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来 m m m 行每行包含三个正整数 u i , v i , w i u_i,v_i,w_i ui,vi,wi,表示第 i i i 条有向边从 u i u_i ui 出发,到达 v i v_i vi,边权为 w i w_i wi(即该边最大流量为 w i w_i wi)。
输出格式
一行,包含一个正整数,即为该网络的最大流。
样例 #1
样例输入 #1
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40- 1
- 2
- 3
- 4
- 5
- 6
样例输出 #1
50- 1
提示
样例输入输出 1 解释
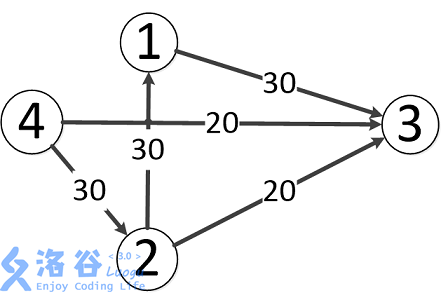
题目中存在 3 3 3 条路径:
- 4 → 2 → 3 4\to 2\to 3 4→2→3,该路线可通过 20 20 20 的流量。
- 4 → 3 4\to 3 4→3,可通过 20 20 20 的流量。
- 4 → 2 → 1 → 3 4\to 2\to 1\to 3 4→2→1→3,可通过 10 10 10 的流量(边 4 → 2 4\to 2 4→2 之前已经耗费了 20 20 20 的流量)。
故流量总计 20 + 20 + 10 = 50 20+20+10=50 20+20+10=50。输出 50 50 50。
数据规模与约定
- 对于 30 % 30\% 30% 的数据,保证 n ≤ 10 n\leq10 n≤10, m ≤ 25 m\leq25 m≤25。
- 对于 100 % 100\% 100% 的数据,保证 1 ≤ n ≤ 200 1 \leq n\leq200 1≤n≤200, 1 ≤ m ≤ 5000 1 \leq m\leq 5000 1≤m≤5000, 0 ≤ w < 2 31 0 \leq w\lt 2^{31} 0≤w<231。
题解(自己去翻)
今天我要水题解!!!
致谢
感谢Sin_又是被迫营业的一天在heheheheehhejie讲过一遍以后,又陪我把代码从头理了一遍。
代码实现
100pts
//洛谷 P3376 【模板】网络最大流 #include#include #include #include using namespace std; long long n,m,s,t; long long u,v,w; int b[210][210]; int cnt=1; int head[210]; int dis[210]; int c[210]; long long ans; long long an; queue<int>q; struct edge{ int v,nex; long long w; }a[10010]; void in(long long &x){ int nt; x=0; while(!isdigit(nt=getchar())); x=nt^'0'; while(isdigit(nt=getchar())){ x=(x<<3)+(x<<1)+(nt^'0'); } } bool bfs(){ memset(dis,-1,sizeof(dis)); dis[s]=1; q.push(s); while(!q.empty()){ int x=q.front(); q.pop(); for(int i=head[x];i;i=a[i].nex){ if(dis[a[i].v]==-1&&a[i].w>0){ dis[a[i].v]=dis[x]+1; q.push(a[i].v); } } } if(dis[t]==-1){ return 0; } return 1; } long long dfs(int x,long long minn){ if(x==t){ return minn; } int an,k=0; for(int i=(c[x]==-1?head[x]:c[x]);i;i=a[i].nex){ if(dis[a[i].v]==dis[x]+1&&a[i].w>0){ minn=min(a[i].w,minn); an=dfs(a[i].v,minn); if(an==0){ dis[a[i].v]=-1; } if(an){ a[i].w-=an; a[i^1].w+=an; c[x]=i; k+=an; minn-=k; return an; } } } return k; } int main(){ register int i; in(n),in(m),in(s),in(t); for(i=1;i<=m;++i){ in(u),in(v),in(w); if(b[u][v]){ a[b[u][v]].w+=w; } else{ b[u][v]=++cnt; a[cnt].v=v; a[cnt].w=w; a[cnt].nex=head[u]; head[u]=cnt; b[v][u]=++cnt; a[cnt].v=u; a[cnt].nex=head[v]; head[v]=cnt; } } while(bfs()){ memset(c,-1,sizeof(c)); an=dfs(s,0xffffffff); while(an){ ans+=an; an=dfs(s,0xffffffff); } } printf("%lld\n",ans); return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
-
相关阅读:
链接脚本和可执行文件
prometheus中PromQL查询语言
python进阶(28)import导入机制原理
Mac管理Ruby环境
计算机操作系统详解
SwiftUI Swift 内功之 Swift 中的属性观察者 didSet 与 willSet
Uni-app中实现数据选择并回传给上个页面的方法
基于Java毕业设计大学生兼职网站源码+系统+mysql+lw文档+部署软件
【深度学习】torch.argmax()函数讲解 | pytorch
计算机毕业设计JavaOA办公系统设计与实现(源码+系统+mysql数据库+lw文档)
- 原文地址:https://blog.csdn.net/AmyLiu_1020/article/details/127464687
