贪心算法的高逼格应用——Huffman编码

14天阅读挑战赛
努力是为了不平庸~
 

Huffman编码

        在计算机的世界里，通常的编码方法有固定长度编码和不等长度编码两种。采用不等长度编码能使总码长度较短。
        Huffman编码利用字符的使用频率来编码，是不等长编码方法，它使得经常使用的字符编码较短，不常使用的字符编码较长。这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。
        例如，在英文中，e的出现机率最高，而z的出现概率则最低。当利用Huffman编码对一篇英文进行压缩时，e极有可能用一个比特来表示，而z则可能花去25个比特（不是26）。用普通的表示方法时，每个英文字母均占用一个字节，即8个比特。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。
        除了使编码尽可能短，不等长编码还需解决另外一个问题，即不能有二义性，例如，ABCD四个字符如果编码如下：

    A:0
    B:1
    C:01
    D:10

那么现在有一列数0110，该怎样翻译呢? 是翻译为ABBA，ABD，CBA，还是CD? 那么如何消除二义性呢? 解决的办法是任何一个字符的编码不能是另一个字符编码的前缀，即前缀码特性。
        哈夫曼编码很好地解决了上述关键问题，被广泛应用于数据压缩，尤其是远距离通信和大容量数据存储方面。

算法详解

        Huffman编码的基本思想是以字符的使用频率作为权值构建一棵Huffman树，然后利用Huffman树对字符进行编码。构造一棵Huffman树，是将所要编码的字符作为叶子结点，该字符在文件中的使用频率作为叶子结点的权值，以自底向上的方式，通过n-1次的“合并”运算后构造出的一棵树，核心思想是权值越大的叶子离根越近。

回到本文题目，那贪心算法和Huffman编码有什么关系呢？

Huffman算法在构建Huffman树时采用的就是贪心策略，每次从树的集合中取出没有双亲且权值最小的两棵树作为左右子树，构造一棵新树，新树根节点的权值为其左右孩子结点权值之和，将新树插入到树的集合中，求解步骤如下。
(1) 确定合适的数据结构。编写程序前需要考虑的情况有：
● Huffman树是二叉树，树中没有度为1的结点，则一棵有n个叶子结点的Huffman树共有 2n-1 个结点 ( n-1 次的“合并”，每次产生一个新结点)。
● 构成Huffman树后，为求编码，需从叶子结点出发走一条从叶子到根的路径。
● 译码需要从根出发走一条从根到叶子的路径，那么我们需要知道每个结点的权值、双亲、左孩子、右孩子和结点的信息。
(2) 初始化。构造n棵结点为n个字符的单结点树集合，每棵树只有一个带权的根结点，权值为该字符的使用频率。
(3) 如果T中只剩下一棵树，则Huffman树构造成功，跳到步骤(6)。否则，从集合T中取出没有双亲且权值最小的两棵树  和 ，将它们合并成一棵新树，新树的左孩子为，右孩子为，的权值为  和  的权值之和。
(4) 从集合T中删去和，加入到集合T
(5) 重复以上(3)~(4)步。
(6) 约定左分支上的编码为“0”，右分支上的编码为“1”。从叶子结点到根结点逆向求出每个字符的Huffman编码，从根结点到叶子结点路径上的字符组成的字符串为该叶子结点的Huffman编码。算法结束。

构建Huffman树的过程图解如下

 

 

 

 

 

 

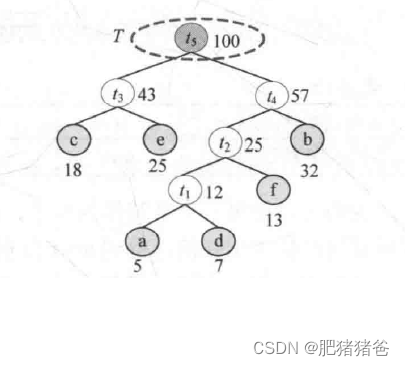
代码

说明
(1) 节点数组前n项是要进行编码的字符，后面n-1项是通过n-1次合并后产生的非叶子节点

(2) 由于节点数组前n项是要进行编码的字符，故通过Huffman树获得编码时，只需遍历节点数组前n项即可

节点数组初始如下：

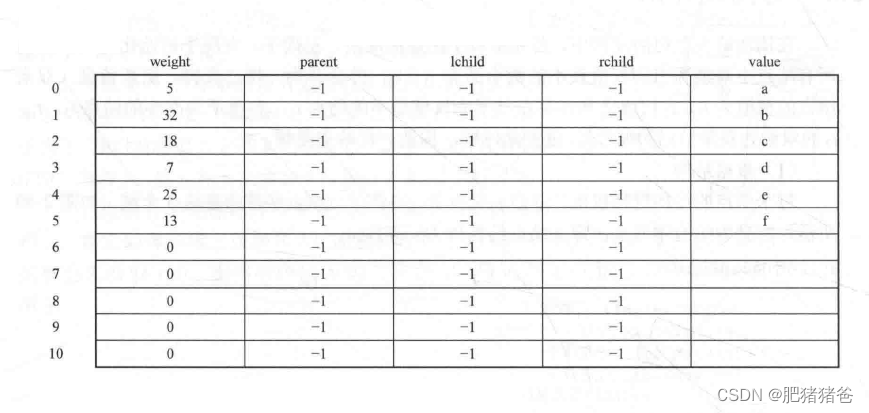
import sys
 
 
# Huffman节点类
class HuffmanNode:
    def __init__(self, weight=0, parent=-1, left_child=-1, right_child=-1, value=""):
        # 权重
        self.weight = weight
        # 父节点索引
        self.parent = parent
        # 左孩子节点索引
        self.left_child = left_child
        # 右孩子节点索引
        self.right_child = right_child
        # 代表的字符
        self.value = value
 
    def __str__(self):
        return "weight:{}, parent:{}, left_child:{}, right_child:{}, value:{}".format(self.weight, self.parent, self.left_child, self.right_child, self.value)
 
 
# 构造Huffman树
def huffman_tree(nodes, num):
    # 需要构建的非叶子节点有N-1个,均排在节点数组后面,故须循环N-1次
    for i in range(num-1):
        # 最小的两个权值,这里m1小于等于m2
        m1 = m2 = sys.maxsize
        # 最小权值节点对应的索引
        x1 = x2 = -1
        # 循环当前所有可用的节点
        for j in range(num + i):
            if(nodes[j].weight < m1 and nodes[j].parent==-1):
                m2 = m1
                x2 = x1
                m1 = nodes[j].weight
                x1 = j
            elif(nodes[j].weight < m2 and nodes[j].parent==-1):
                m2 = nodes[j].weight
                x2 = j
        # 给需要合并成树的子节点设置父节点索引
        nodes[x1].parent = num + i
        nodes[x2].parent = num + i
        # 给合并成树的父节点设置子节点信息
        nodes[num + i].left_child = x1
        nodes[num + i].right_child = x2
        nodes[num + i].weight = m1 + m2
 
 
# 通过Huffman树获得Huffman编码
def huffman_code(nodes, num):
    # 最终结果
    huff_codes = dict()
    # 循环所有的叶子节点,叶子节点都在节点数组前面
    for i in range(num):
        # 该叶子节点对应的编码数组
        leaf_code = []
        # 当前节点索引
        c = i
        # 父节点索引
        p = nodes[i].parent
        while p != -1:
            # 当前节点是父节点的左孩子,编码为0,当前节点是父节点的右孩子,编码为1
            if nodes[p].left_child == c:
                leaf_code.insert(0, 0)
            elif nodes[p].right_child == c:
                leaf_code.insert(0, 1)
            # 将当前节点和父节点沿路径上移
            c = p
            p = nodes[c].parent
        
        if len(leaf_code)>0:
            huff_codes[nodes[i].value] = "".join(str(lc) for lc in leaf_code)
    return huff_codes
 
 
# 算法主体
def run():
    N = 6
    # 初始化节点数组,对N个元素进行编码,则Huffman树的节点数是2N-1
    nodes = [HuffmanNode() for _ in range(2*N - 1)]
    # 初始化叶子节点
    nodes[0].weight = 5
    nodes[0].value = "a"
    nodes[1].weight = 32
    nodes[1].value = "b"
    nodes[2].weight = 18
    nodes[2].value = "c"
    nodes[3].weight = 7
    nodes[3].value = "d"
    nodes[4].weight = 25
    nodes[4].value = "e"
    nodes[5].weight = 13
    nodes[5].value = "f"
    # 构建Huffman树 
    huffman_tree(nodes, N)
    # 从Huffman树中获得叶子节点的Huffman编码
    result = huffman_code(nodes, N)
    
    for r in result:
        print("{} 的 Huffman编码是:{}".format(r, result[r]))
 
 
if __name__ == "__main__":
    run()

程序运行结果如下

a 的 Huffman编码是:1000
b 的 Huffman编码是:11
c 的 Huffman编码是:00
d 的 Huffman编码是:1001
e 的 Huffman编码是:01
f 的 Huffman编码是:101

作者这水平有限，有不足之处欢迎留言指正