经典论文回顾：Decomposing Images into Layers via RGB-space Geometry

论文：Decomposing Images into Layers via RGB-space Geometry 发表于ACM TOG 2016，是第一个基于RGB凸包的调色板图像编辑算法，我近两年的研究跟本文有很大关系，因此这里再次回顾一下这篇经典论文。

本文目标是对于给定图像提取出调色板，计算对应的半透明图层，并期望通过这些图层完美重建出输入图像，下图展示了该方法的输入和输出。

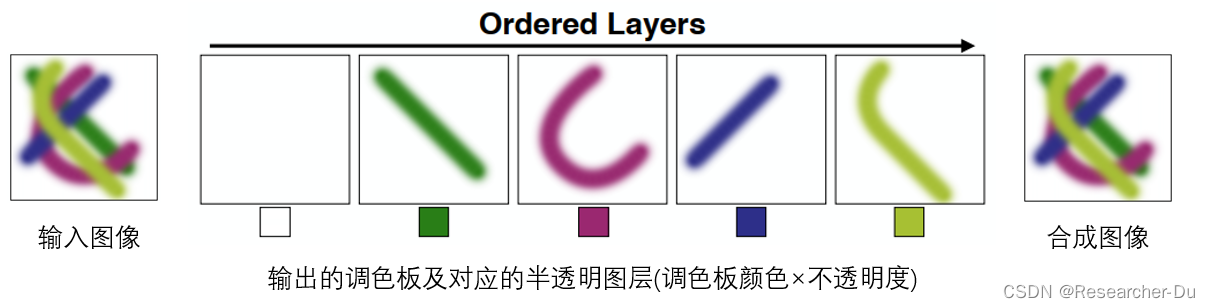
算法分为两步：1）计算初始调色板和简化；2）计算调色板对应的半透明图层. 下面做详细分析.

一、计算初始调色板

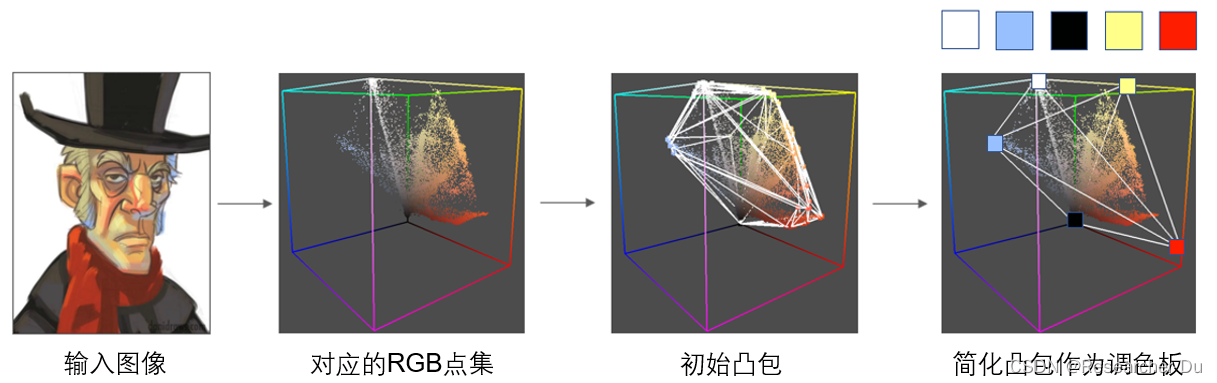
初始调色板的求解过程如下图所示，分为三个步骤：

• （1）将图像投影到RGB空间,颜色为(r,g,b)的像素对应RGB空间下的3D点p(r,g,b). 因此，整个图像对应RGB空间下的一个点集；
• （2）求解该点集的初始凸包，但初始凸包拓扑复杂，顶点较多，需要进一步简化。
• （3）最后，将简化凸包作为图像的调色板。
  

简化初始凸包

那么，如何简化上图第3列所示的初始凸包呢？本文通过缩边的方式对原始凸包进行简化，迭代的将边缩减为点，每次缩边操作使得体积增加。如下图所示，主要分为三步：

• 1）计算每条边收缩为点后凸包体积的增量;
• 2）选择增量最小的边进行收缩, 每次缩边使得顶点数目减一;
• 3）重复上述过程，直到凸包顶点数目缩减到给定值.
• 4）将简化凸包的顶点作为图像调色板.
  

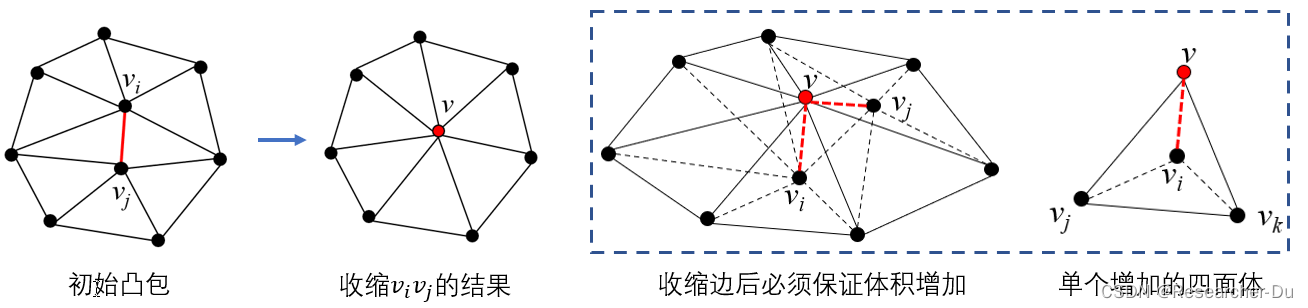
那么，对于某一条候选边，如何计算缩边带来的体积增量呢？

对于每条候选边 $v_i{v}_j$，收缩为点 $v$ 后体积的增量如上图第3列所示，连接 $v{v}_i$ 和 $v{v}_j$, 增加的体积可剖分为多个四面体，上图第4列就是上图第3列正前方的四面体。该四面体的体积可表示为：
$$A/3\cdot \mathbf{n}\cdot (v-v_i)\text{\hspace{1em}(0)}$$
其中, $A$表示$△v{v}_j{v}_k$的面积， $\mathbf{n}$表示$△v{v}_j{v}_k$朝外的法向量，$v$表示待求顶点。那么，整体的体积增量就是多个四面体的体积，我们的目标是得到一个使得整体体积增加最小的 $v$, 因此可以通过最下化如下所式的能量函数求解：
$$v=argmin\sum \frac{A}{3}\mathbf{n}\cdot (v-v_x)s.t.\frac{A}{3}\mathbf{n}\cdot (v-v_x)>0\text{\hspace{1em}(1)}$$
其中，$v_x$ 可能是 $v_i$ 或 $v_j$， 根据不同的四面体而定，上述能量函数可以通过线性优化求解。
凸包简化效果如下图所示，凸包简化到什么程度由用户决定, 若用户决定简化到5个顶点，则得到左下角所示的调色板.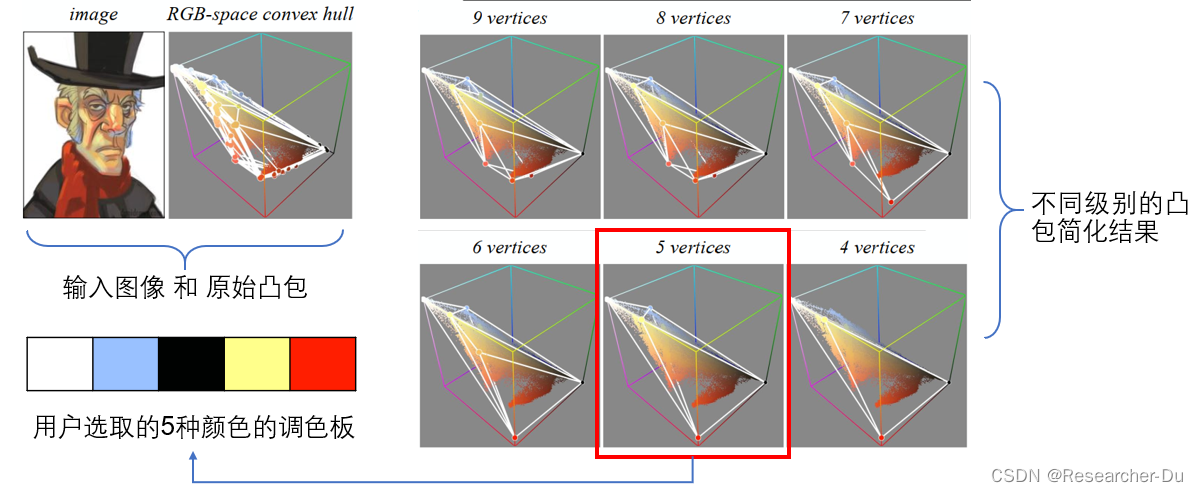

二、图层不透明度计算

本文使用Porter-Duff “Over” 颜色混合模式进行颜色混合，也就是常用的alpha-blending, 其颜色混合模式为：
$$After=Paint\cdot \alpha +Before\cdot (1-\alpha )\text{\hspace{1em}(2)}$$
其中，$Paint$ 表示前景图层，$Before$ 是背景图层，$After$ 是背景和前景混合后的颜色. 可以看出合成的颜色跟图层的顺序和不透明度有关. 本文采用这种颜色混合模式，也就是说，图像中任意像素的颜色可以通过给定的顺序的调色板颜色 和 不透明度 经alpha-blending混合得到。 下图给出了这个问题的描述：

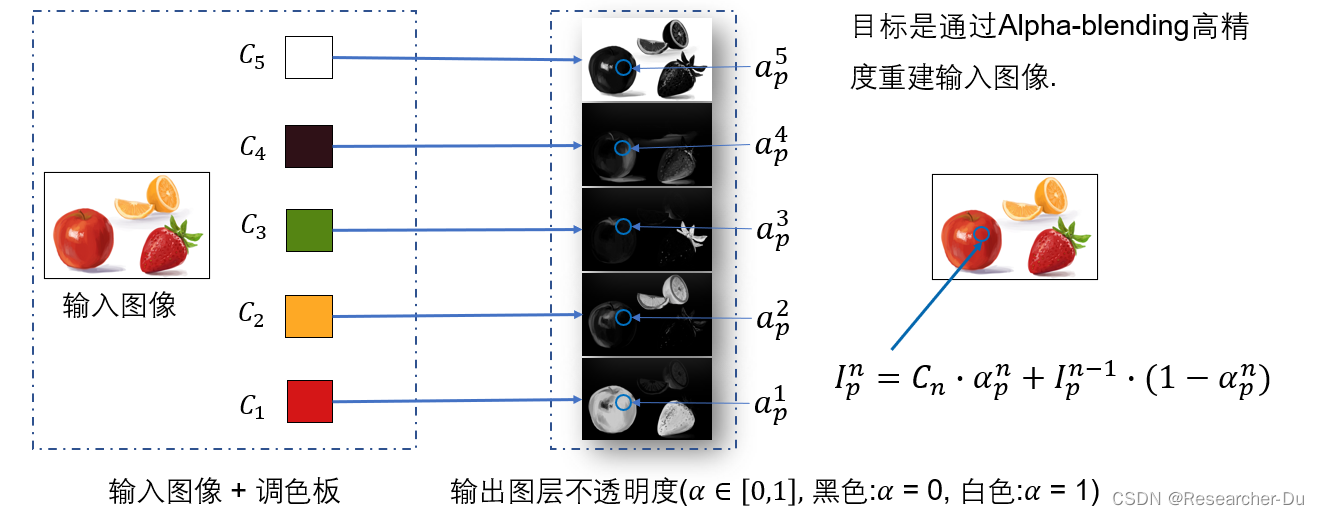
本文图层的概念：图层数目跟调色板颜色数目相同，图层的尺寸跟输入图像一致，图层中每个位置的数值 $a_p^i$ 表示合成像素$p$的颜色$C_i$对应的不透明度, $0(黑色)<=a_p^i<=1（白色）$.

我们注意到，alpha-blending这种颜色混合模式跟图层的顺序有直接关系，针对给定调色板$C=C_1,C_2,...C_n$, 颜色排列有𝑛!种. 如下图所示，给定不同的调色板顺序得到的图层均可重建图像.因此, 本文由用户指定调色板颜色顺序.

但即便如此，对于给定的调色板顺序，每个像素点关于各个调色板颜色对应的不透明度仍有无穷解。也就是说，针对任一点 $p$, 它可能被多种方式进行重建：
p = A l p h a B l e n d i n g ( { C 1 , a p 1 } , { C 2 , a p 2 } , . . . { C n , a p n } ) = A l p h a B l e n d i n g ( { C 1 , b p 1 } , { C 2 , b p 2 } , . . . { C n , b p n } ) . . . p = AlphaBlending(\{C_1,a^1_p\},\{C_2,a^2_p\},...\{C_n,a^n_p\}) = AlphaBlending(\{C_1,b^1_p\},\{C_2,b^2_p\},...\{C_n,b^n_p\})... p=AlphaBlending({C1​,ap1​},{C2​,ap2​},...{Cn​,apn​})=AlphaBlending({C1​,bp1​},{C2​,bp2​},...{Cn​,bpn​})...
其中，$a_p^i$ 表示合成 $p$ 的调色板颜色 $C_i$对应的不透明度， { a p i } \{a^i_p\} {api​} 和 { b p i } \{b^i_p\} {bpi​} 表示两组不同的解，这种解其实有无穷组. 为了说明这个问题，如下所示，我们给定一个凸包（调色板）并给定颜色顺序 $c_0,c_1,c_2,c_3,c_4$， 以及待合成的d顶点(颜色) $P$, 下图中的两条路径对应了两种不同的解.

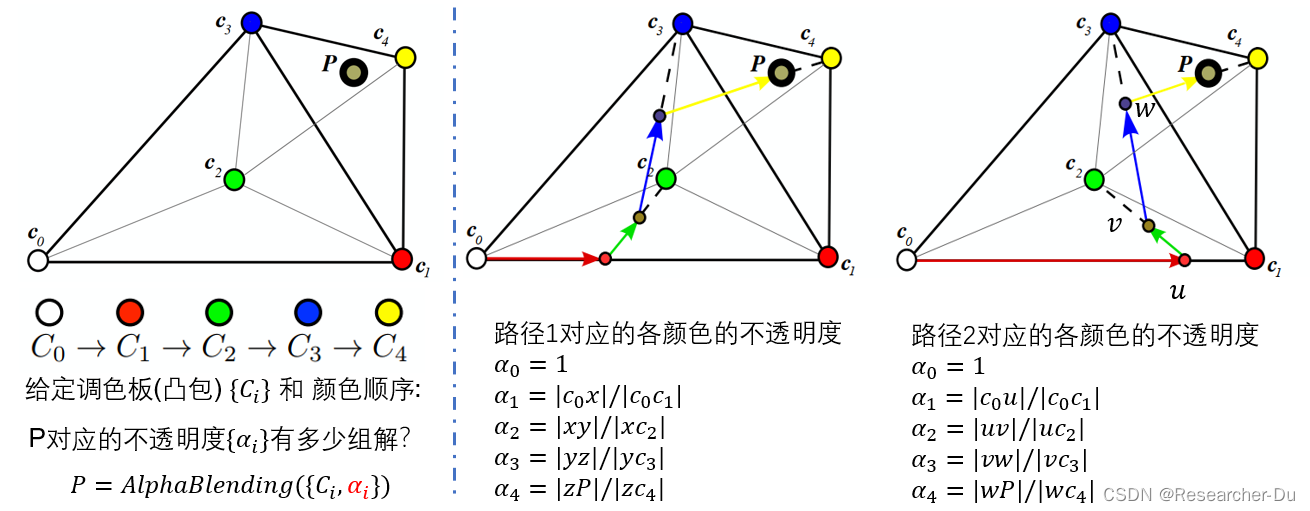
那么，对于给定的调色板颜色顺序，如何确定每个像素的对应的多个不透明度呢？本文提出两种策略, 分别是1）基于广义重心坐标的算法和 2）基于能量优化的算法。接下来，对这两种算法简单介绍.

2.1 基于广义重心坐标的算法求解不透明度

我们注意到alpha blending的颜色混合模式：
$$I_p^n=C_n\cdot {\alpha }_p^n+I_p^{n-1}\cdot (1-{\alpha }_p^n)\text{\hspace{1em}(3)}$$
可以等效的表示为：
$$I_p^n=\sum _{i=1}^n{w}_i{C}_i\text{\hspace{1em}(4)}$$

我们知道(3)(4)均对应无穷解，但是如果我们能通过别的方法确定（3）的唯一一组权重，那么我们可以恢复出（2）的不透明度：
α p i = { 1 − ∑ j = 1 i − 1 w j ∑ j = 1 i w j      , ∑ j = 1 i w j > 0 0      , 𝑜 𝑡 h 𝑒 𝑟 𝑤 𝑖 𝑠 𝑒 (5) \alpha^i_p=\left\{

\right.\tag5 αpi​=⎩ ⎨ ⎧​1−∑j=1i​wj​∑j=1i−1​wj​​    ,j=1∑i​wj​>00    ,otherwise​(5)
本文采用ASAP（As sparse as possible ）的算法对凸包内部的像素点进行插值，具体而言，将凸包进行四面体剖分,每个像素点𝑃可以唯一表示成所在四面体顶点𝐴𝐵𝐶𝐷的凸组合：$P=w_{A}A+w_{B}B+w_{C}C+w_{D}D,w_A+w_B+w_C+w_D=1$

当然，也可以使用别的广义重心坐标算法，比如：
[1] Mean value coordinates for closed triangular meshes[J]. Ju et.al. ACM Transactions on Graphics, 2005.
[2] Local Barycentric Coordinates, Zhang et.al. ACM Transactions on Graphics, 2014.

2.2 基于能量优化的算法求解不透明度

本质上，公式（2）是一个欠约束的问题，当调色板的颜色数目超过图像的颜色通道时必然有无穷解，为此可以构造带约束的能量优化函数，并通过最小化能量函数求解不同明度:
$$E=w_r{E}_r+w_o{E}_o+w_s{E}_s\text{\hspace{1em}(6)}$$
其中，$E_r$ 表示重建误差，定义如下所示，$K$表示颜色通道数目.
$$E_r=\frac{1}{K}||I_p^n-I_p|{|}^2\text{\hspace{1em}(7)}$$
其中，$E_o$ 表示不透明度约束，目的是惩罚较大的不透明度，定义为：
$$E_o=\frac{1}{n}\sum _{i=1}^n-(1-{\alpha }_i{)}^2\text{\hspace{1em}(8)}$$
其中，$E_s$ 表示光滑性约束，目的是保证相似的像素具有相似的不透明度，定义为：
$$E_s=\frac{1}{n}\sum _{i=1}^n-(\nabla {\alpha }_i{)}^2\text{\hspace{1em}(9)}$$
然后，直接求解即可得到多个图层，per-pixel的不透明度。

三、实验效果

1）图层分解示例：这里的图层是 调色板颜色 × 不透明 的结果。

2）不同的图层不透明算法的比较

3）重着色编辑结果，需要注意的是，重着色结果保持图层不透明度不变，只是改变调色板颜色进行重新alpha-blending即可。