数据结构实验4 二叉搜索树与平衡二叉树（C语言实现+详细注释）

题目要求

分别实现二叉搜索树和平衡二叉树的创建、插入和查找操作.

输入

第一行是一个整数n，表示后面有n个整数按顺序分别插入一棵二叉搜索树和一棵平衡二叉树。例如：

3
10 20 30

表示分别向二叉搜索树和平衡二叉树按输入顺序插入3个结点，结点的元素值分别是10、20、30。因此，构建完成的二叉搜索树和平衡二叉树分别为：

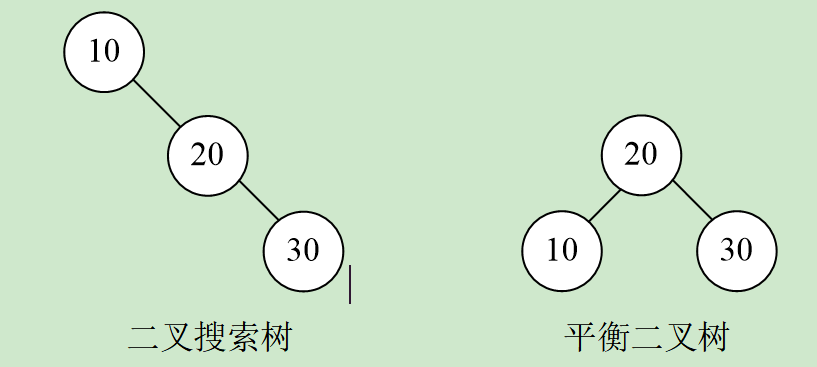
输出

分别在两棵树中对所有元素执行查找操作，统计查找过程中进行比较的总次数，分两行输出。例如，对于上面的示例输入，输出为：

6
5

说明：第1行的6表示在二叉搜索树中，查找10这个元素需要比较1次，查找20这个元素需要比较2次，查找30这个元素需要比较3次，因此总共是6次；第2行的5表示在平衡二叉树中国，查找10这个元素需要比较2次，查找20这个元素需要比较1次，查找30这个元素需要比较2次，因此总共是5次。

代码实现

树的定义

二叉搜索树和平衡二叉树用同一个结构体，毕竟平衡二叉树也是一种二叉搜索树。

typedef struct BinTreeNode {
    int data;
    struct BinTreeNode* left;
    struct BinTreeNode* right;
}*BinTree;
typedef BinTree AVLTree;
1
2
3
4
5
6

插入元素

插入操作在浙大版《数据数据》上都有完整代码，我的实现与书中大致相同。

1.二叉搜索树的插入

/* 二叉搜索树 */
BinTree BT_Insert(BinTree binTree, int data) {
    if (!binTree) {
        binTree = (BinTree)malloc(sizeof(struct BinTreeNode));
        binTree->data = data;
        binTree->left = binTree->right = NULL;
    } else {
        if (binTree->data > data)
            binTree->left=BT_Insert(binTree->left, data);
        else if (binTree->data < data)
            binTree->right=BT_Insert(binTree->right, data);
    }
    return binTree;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.平衡二叉树的插入

我之前这篇博客里有对平衡二叉树的相关实现，不懂平衡二叉树的小伙伴可以看一看：传送门
具体逻辑看注释。

/* 平衡二叉树 */
int max(int a, int b) {
    return a > b ? a : b;
}
int getHeight(BinTree tree) {
    return tree ? max(getHeight(tree->left), getHeight(tree->right)) + 1 : 0;
}
/*针对左左局面做顺时针旋转*/
AVLTree leftLeft(AVLTree avlTree) {
    AVLTree leftChild = avlTree->left;
    avlTree->left = leftChild->right;
    leftChild->right = avlTree;
    return leftChild;
}
/*针对右右局面做逆时针旋转*/
AVLTree rightRight(AVLTree avlTree) {
    AVLTree rightChild = avlTree->right;
    avlTree->right = rightChild->left;
    rightChild->left = avlTree;
    return rightChild;
}
/*针对左右局面做双旋*/
AVLTree leftRight(AVLTree avlTree) {
	// 对avlTree的左孩子进行逆时针旋转（可以把avlTree的左孩子看作处于相对的右右局面（不是真正的右右局面））
    avlTree->left = rightRight(avlTree->left);
    // 上一步操作后，树变成了左左局面
    return leftLeft(avlTree);
}
/*针对右左局面做双旋*/
AVLTree rightLeft(AVLTree avlTree) {
	// 对avlTree的右孩子进行顺时针旋转
    avlTree->right = leftLeft(avlTree->right);
    // 上一步操作后，树变成了右右局面
    return rightRight(avlTree);
}
AVLTree AVL_Insert(AVLTree avlTree, int data) {
    if (!avlTree) {
        avlTree = (AVLTree)malloc(sizeof(struct BinTreeNode));
        avlTree->left = avlTree->right = NULL;
        avlTree->data = data;
    } else {
        if (data > avlTree->data) {
            avlTree->right = AVL_Insert(avlTree->right, data);
            if (getHeight(avlTree->right) - getHeight(avlTree->left) == 2)
                avlTree = data > avlTree->right->data ? rightRight(avlTree) : rightLeft(avlTree);
                // 一开始我还以为data就是一定等于avlTree的右孩子的data。
                // 但是上一步insert后，data就不是avlTree的右孩子的data,即使insert的参数的avlTree的右孩子；data已经是avlTree的右孩子的左右孩子中的一个data。因为上一步insert已经跳出了，树的结构改变了
                // 自己简单走一遍递归流程就能理解的
                // 如果data大于avlTree的右孩子的data，说明带这个data的节点变成了avlTree的右孩子的右孩子，此时的树是右右局面
                // 如果data小于avlTree的右孩子的data，说明带这个data的节点变成了avlTree的右孩子的左孩子，此时的树是右左局面
        } else if (data < avlTree->data) {
            avlTree->left = AVL_Insert(avlTree->left, data);
            if (getHeight(avlTree->left) - getHeight(avlTree->right) == 2)
                avlTree = data < avlTree->left->data ? leftLeft(avlTree) : leftRight(avlTree);
        }
    }
    return avlTree;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

获取搜索次数

在遍历的基础上对每一个节点单独获取搜索次数，然后累加即可。我在这里用了非递归的前序遍历，需要用到栈来辅助一波。

栈的定义

typedef BinTree SElementTYpe;
typedef struct StackNode {
    SElementTYpe data;
    struct StackNode* next;
    int flag;
}*Stack;
Stack createStack() {
    Stack stack = (Stack)malloc(sizeof(struct StackNode));
    stack->next = NULL;
    return stack;
}
int isEmpty(Stack stack) {
    return stack->next == NULL;
}
void push(Stack stack, SElementTYpe data) {
    Stack newNode = (Stack)malloc(sizeof(struct StackNode));
    newNode->data = data;
    newNode->next = stack->next;
    stack->next = newNode;
}
SElementTYpe pop(Stack stack) {
    if (isEmpty(stack))
        return NULL;
    Stack top = stack->next;
    SElementTYpe data = top->data;
    stack->next = top->next;
    free(top);
    return data;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

非递归前序遍历实现+获取搜索次数

getSearchCount方法用于获取树的某个节点的搜索次数，把每个节点遍历一次，分别调用这个方法，将搜索次数累加起来返回即可。

这段非递归遍历的代码在浙大版《数据结构》书上也是有的，不超纲。

int getSearchCount(BinTree binTree, int data) {
    int searchCount = 0;
    while (binTree) {
        searchCount++;
        if (binTree->data > data)
            binTree = binTree->left;
        else if (binTree->data < data)
            binTree = binTree->right;
        else
            break;
    }
    return searchCount;
}
int preorderTraversal(BinTree binTree) {
    int totalSearchCount = 0;
    Stack stack = createStack();
    BinTree bt = binTree;
    while (bt || !isEmpty(stack)) {
        while (bt) {
            totalSearchCount += getSearchCount(binTree, bt->data);
            push(stack, bt);
            bt = bt->left;
        }
        bt = pop(stack);
        bt = bt->right;
    }
    return totalSearchCount;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

主函数

对输入的数据分别调用相应的插入方法来构建二叉搜索树、平衡二叉树，然后在分别调用preorderTraversal方法获得搜索总次数就ok了。
我在主函数这里踩了个小坑，没有把binTree、avlTree都赋值为NULL，导致无法正常创建树。

int main() {
    BinTree binTree = NULL;
    AVLTree avlTree = NULL;
    int num, data;
    scanf("%d", &num);
    for (int i = 0;i < num;i++) {
        scanf("%d", &data);
        binTree = BT_Insert(binTree, data);
        avlTree = AVL_Insert(avlTree, data);
    }
    printf("%d\n%d", preorderTraversal(binTree), preorderTraversal(avlTree));
    system("pause");
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

报告里只给出一个测试数据，目前输出结果没问题。能不能ac还得看实验当天了。