分治&暴力求解最近点对问题 + 时间性能量化分析

1 Intro

本文旨在讨论分治和暴力在求解最近点对问题时的时间性能问题，关于解题部分不做过多讲解，只附上相关代码。

2 Problem

给定平面上N个点，找出其中的一对点的距离，使得在这N个点的所有点的对中，该距离为所有点对中最小的。

3 Time performance analysis

测试围绕模拟次数和集合S的规模大小两个维度进行展开进行测试，并分析时间复杂度。

其中集合S存放所有的点信息，S的规模大小即为点的个数

A. 当S大小为100时，采用100次和1000次模拟情况，以程序稳定性、单次耗时和总耗时为评价指标
a.蛮力法
在经过100次和1000次随机测试之后，可以发现大多数的程序单次耗时稳定在0.004s到0.005s之内。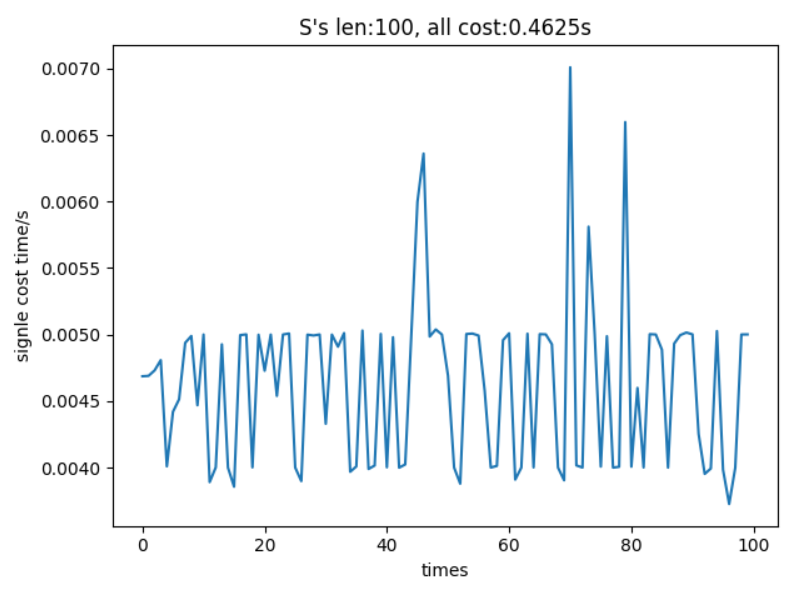

图为100次len(S)=100模拟测试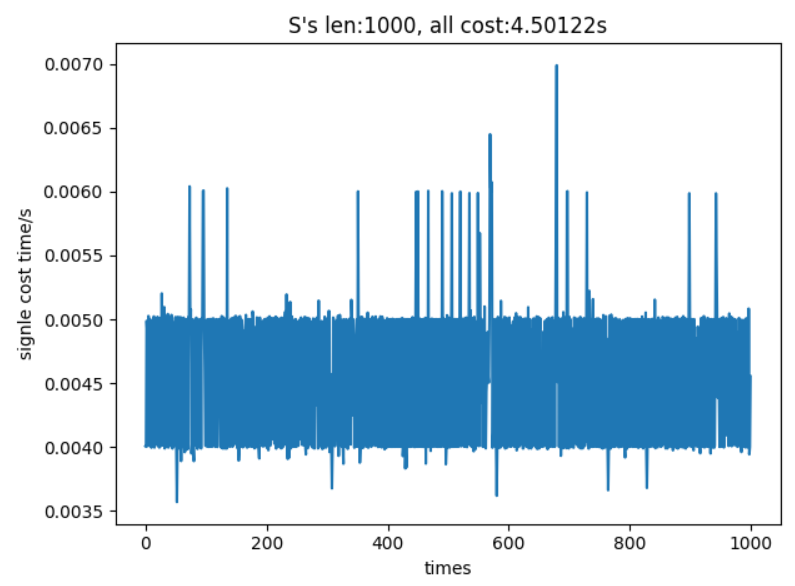

图为1000次len(S)=100模拟测试

b. 分治法
在经过100次和1000次随机测试之后可以看出，大多数测试用例的单次耗时维持在0.01s~0.014s之间，但从总体的稳定性不如蛮力法，可以看出不同类型的测试用例对分治法的影响大于对蛮力法的影响。
从平均耗时可以看出，在S=100的数量级下，分治法的效果不如蛮力法。

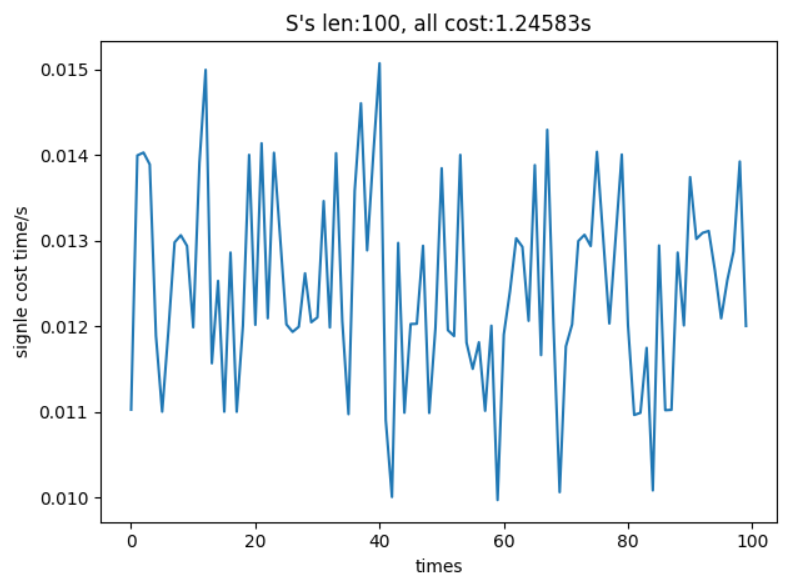
图为100次len(S)=100模拟测试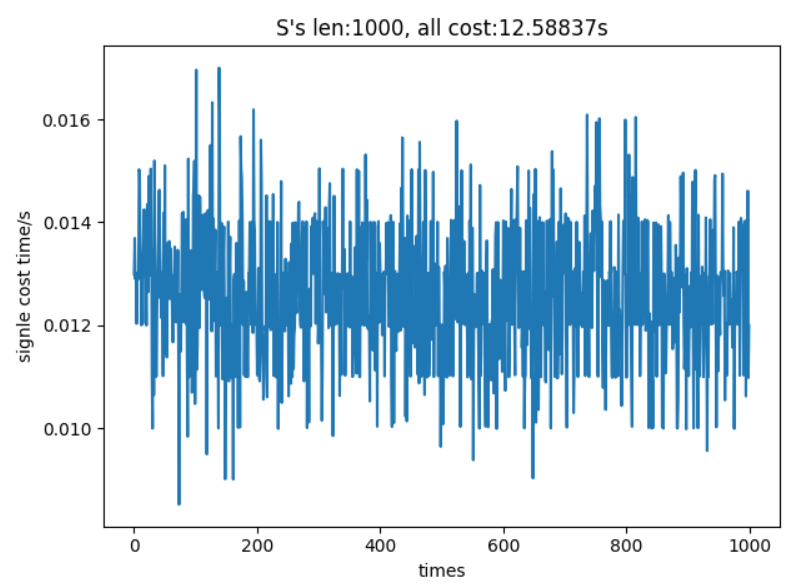

图为1000次len(S)=100模拟测试

B. 当模拟次数固定为100时，采用len(S)=100和len(S)=1000进行模拟，以程序稳定性、单次耗时和总耗时为评价指标。
a.分治法

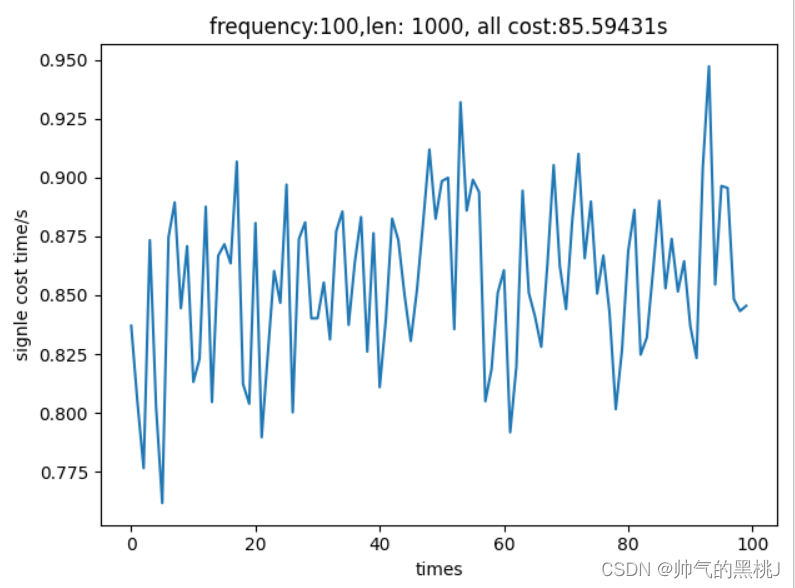
b.蛮力法
可以发现，在集合S由100变为1000之后，总体耗时增加了，最低耗时由之前的0.004s变为现在的0.44s，时间上的稳定性也下降了，但总体维持在合理的耗时区间内，较为稳定。

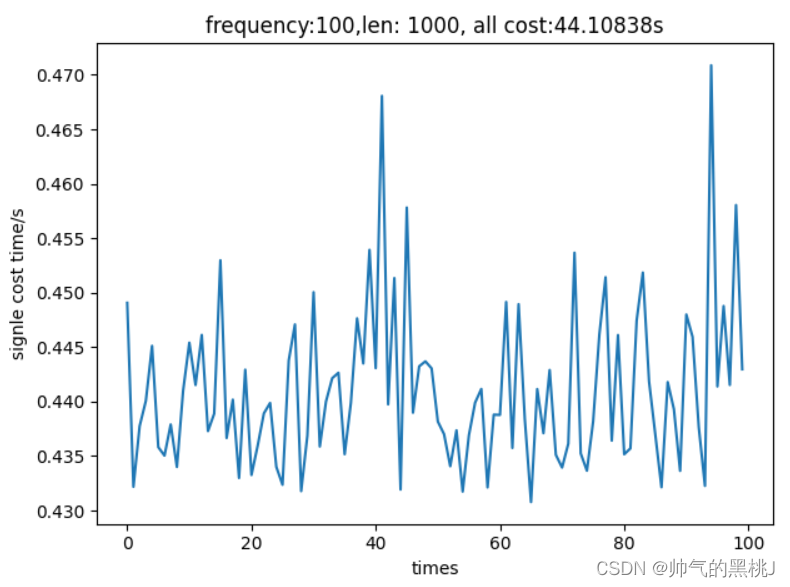
图为100次len(S)=1000模拟测试

C. 时间复杂度分析
蛮力法
蛮力法需要两边for循环，因此时间复杂度为O(n^2)，在实际模拟验证的情况下也确实如此，如下图所示。

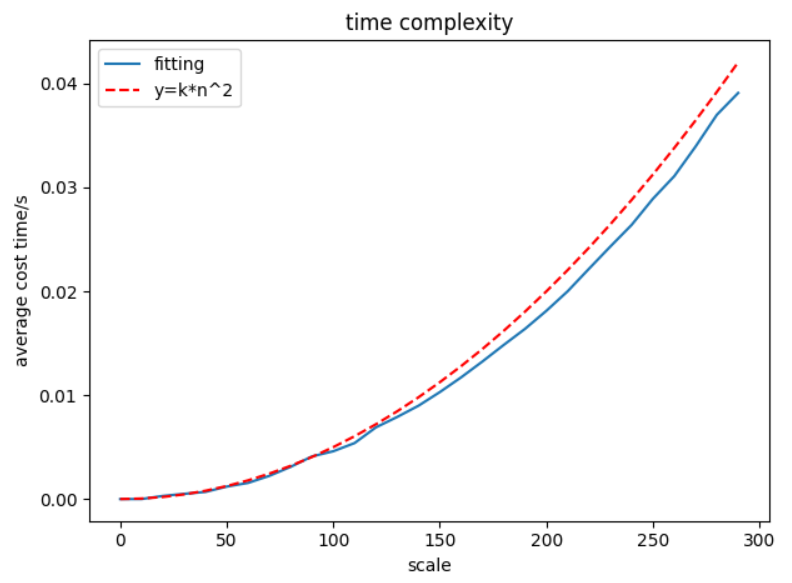
图为使用蛮力法的时间复杂度

分治法
在程序的分治过程中，采用了O(nlogn)时间，程序中部分地方为预排序时间，不算在算法中。当n>3时满足递归方程 T(n) = 2T(n/2) + O(n)，因此，有T(n)=O(nlogn)

事实上上面是理论分析，下面展现实际运行情况。

下图为1000次模拟时的分治法运行情况，说实话，我用了几种函数，并不能很好的拟合这种情况，原因有二：其一，测试规模过小，只有1000，但是事实上本人的计算机跑了1000次也花了几分钟时间，较为耗时，有兴趣的朋友可以尝试扩大数据的规模进一步的测试；其二，在测试规模没有达到一定程度时，时间复杂度最高阶部分的耗时并不能显著的体现出来，这也就是为什么这个曲线看起来奇奇怪怪的原因了。

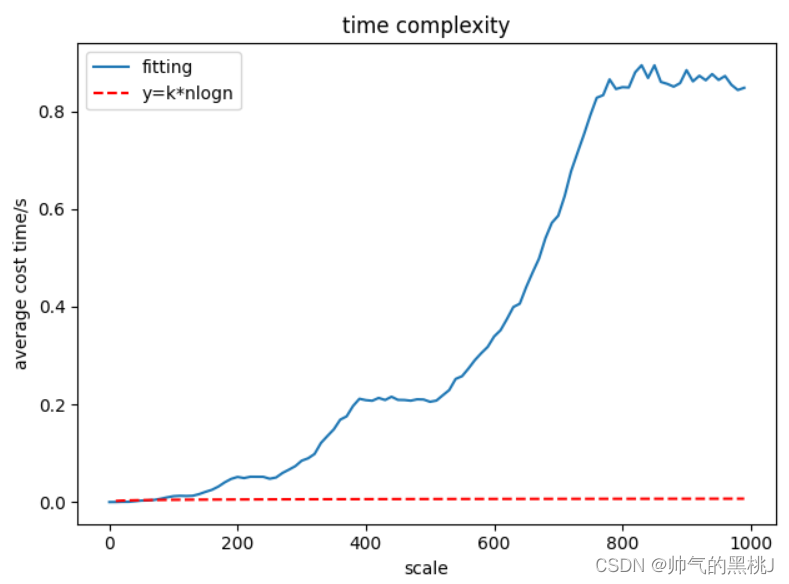
笔者在这里并没有做深入的时间性能分析，如果大家有更好的想法，欢迎提出来，想要分析部分的全部代码可以私聊笔者。

4 Solution

直接附上求解代码

分治法
代码如下所示：

import math
import time

class SolutionByDivide:
    def find_nearest_direction(self, p: list):
        start_time = time.time()
        n = len(p)
        p.sort()
        min_dir, min_p = divide(0, n - 1, [], p, n)

        return min_dir, min_p, time.time() - start_time

# 查找最接近的目标的y下标
def find_closed_index(collections, target):
    n = len(collections)
    low = 0
    high = n - 1
    mid = 0
    while low <= high:
        mid = math.floor((low + high) / 2)
        if target > collections[mid][1]:
            low = mid + 1
        elif target < collections[mid][1]:
            high = mid - 1
        else:
            return mid
    return mid

def distance(p1, p2):
    return math.sqrt(pow(p1[0] - p2[0], 2) + pow(p1[1] - p2[1], 2))


def divide(l, r, res, p, n):
    if l == r:
        return float("inf"), []
    if (l + 1) == r:
        return distance(p[l], p[r]), [p[l], p[r]]
    mid = math.floor((l + r) / 2)
    d1, res1 = divide(l, mid, res, p, n)
    d2, res2 = divide(mid + 1, r, res, p, n)
    if d1 >= d2:
        d = d2
        res = res2
    else:
        d = d1
        res = res1

    # 先将所有左子域、右子域、同一x值的中间子域，删选出来
    left = []
    right = []
    midd = []
    b = p[mid][0]
    bl = b - d
    br = b + d
    for i in range(n):
        if ((p[i][0] >= bl) & (p[i][0] <= b)) == True:
            left.append(p[i])
            if p[i][0] == b:
                midd.append(p[i])
        elif ((p[i][0] <= br) & (p[i][0] >= b)) == True:
            right.append(p[i])

    if len(right) == 0:
        return d, res

    # 将右子域先按照y值大小排好序
    right.sort(key=lambda x: x[1])

    # 遍历左子域中的每一个点，在右子域中寻找y值最邻近的四个点，求出最小距离以及最近点对
    for i in range(len(left)):
        closed_point = []
        right_num = len(right)
        if right_num <= 4:
            closed_point = right
        else:
            index = find_closed_index(right, left[i][1])
            if index >= 4:
                start = index - 4
            else:
                start = 0
            if index + 5 > len(right) - 1:
                end = len(right) - 1
            else:
                end = index + 5

            for j in range(start, end):
                closed_point.append(right[j])

            # 前四个就是右子域中离左子域最近的四个点
            closed_point.sort(key=lambda x: abs(x[1] - left[i][1]))

        if len(closed_point) >= 4:
            end2 = 4
        else:
            end2 = len(closed_point)

        for k in range(0, end2):
            dist = distance(closed_point[k], left[i])
            if dist < d:
                res = [closed_point[k], left[i]]
                d = dist

    # 再在中间子域的内部进行比较，看看有没有x值相同，且距离最近的两个点
    if len(midd) > 1:
        midd.sort()
        for j in range(len(midd) - 1):
            dist = distance(midd[j], midd[j + 1])
            if dist < d:
                res = [midd[j], midd[j + 1]]
                d = dist

    return d, res

def single_test(ins):
    p = [[0, 0], [1, 1], [3, 4], [0, 3], [3.2, 4.2], [0, -1], [-2, -2], [-1, -2], [0, 0.4], [-1, 2], [0, 2], [0.5, 2]]
    min_dir, min_p, cost_time = ins.find_nearest_direction(p)
    print('距离最小两个点为:', min_p[0], min_p[1])
    print('距离为:', min_dir)

if __name__ == '__main__':
    ins = SolutionByDivide()

    # single instance
    single_test(ins)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125

运行结果如下所示：

蛮力法
代码如下所示：

# -*- coding: utf-8 -*-
# @Time    : 2022/10/20 15:56
# @Author  : Zeeland
# @File    : 最近点对点问题_暴力.py
# @Software: PyCharm

import math
import time
import random
import matplotlib.pyplot as plt
import numpy as np

class Solution:
    def find_nearest_direction(self, p: list):
        start_time = time.time()
        n = len(p)
        min_dir = float('inf')
        min_p = []
        for i in range(n):
            for j in range(n):
                if j == i:
                    break
                dir = math.sqrt(math.pow(p[i][0]-p[j][0], 2) + math.pow(p[i][1]-p[j][1], 2))
                if dir < min_dir:
                    min_dir = dir
                    min_p = [[p[i]], [p[j]]]
        return min_dir, min_p, time.time() - start_time

def plot_analysis(historty_time: list):
    plt.plot(list(range(len(history_time))), history_time)
    plt.xlabel('times')
    plt.ylabel('signle cost time/s')
    plt.show()

if __name__ == '__main__':
    # single instance
    ins = Solution()
    p = [[0, 0], [1, 1], [3, 4], [0, 3], [3.2, 4.2], [0, -1], [-2, -2], [-1, -2], [0, 0.4], [-1, 2], [0, 2], [0.5, 2]]
    min_dir, min_p, cost_time = ins.find_nearest_direction(p)
    print('距离最小两个点为:', min_p[0][0], min_p[1][0])
    print('距离为:', min_dir)

    # 100 times simulation
    all_cost_time = 0
    history_time = []
    for i in range(100):
        p = [[random.randint(1, 10000), random.randint(1, 100)] for _ in range(100)]
        history_time.append(ins.find_nearest_direction(p)[2])
        all_cost_time += history_time[i]
    print('100次模拟的总时间花费:', all_cost_time,'s')

    # stability analysis
    plot_analysis(history_time)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

运行结果如下所示：

5 Reference

【算法设计与分析】分治法求最近点对问题