【Machine Learning】17.多分类问题

之前说的都是简单的二分类问题，今天扩展到多分类问题

1.导入

import numpy as np
import matplotlib.pyplot as plt
%matplotlib widget
from sklearn.datasets import make_blobs
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
np.set_printoptions(precision=2)
from lab_utils_multiclass_TF import *
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)
1
2
3
4
5
6
7
8
9
10
11
12

2.多分类问题

此类网络的最后一层将有多个单元。每个输出都与一个类别相关联。当输入示例应用于网络时，具有最大值的输出是预测的类别。如果输出应用于softmax函数，则softmax的输出将提供输入在每个类别中的概率。

2.1 加载并可视化数据

加载数据

# make 4-class dataset for classification
classes = 4
m = 100
centers = [[-5, 2], [-2, -2], [1, 2], [5, -2]]
std = 1.0
X_train, y_train = make_blobs(n_samples=m, centers=centers, cluster_std=std,random_state=30)
1
2
3
4
5
6

def plt_mc(X_train,y_train,classes, centers, std):
    css = np.unique(y_train)
    fig,ax = plt.subplots(1,1,figsize=(3,3))
    fig.canvas.toolbar_visible = False
    fig.canvas.header_visible = False
    fig.canvas.footer_visible = False
    plt_mc_data(ax, X_train,y_train,classes, map=dkcolors_map, legend=True, size=50, equal_xy = False)
    ax.set_title("Multiclass Data")
    ax.set_xlabel("x0")
    ax.set_ylabel("x1")
    #for c in css:
    #    circ = plt.Circle(centers[c], 2*std, color=dkcolors_map(c), clip_on=False, fill=False, lw=0.5)
    #    ax.add_patch(circ)
    plt.show()

plt_mc(X_train,y_train,classes, centers, std=std)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

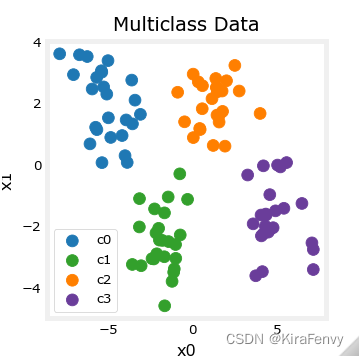
# show classes in data set
print(f"unique classes {np.unique(y_train)}")
# show how classes are represented
print(f"class representation {y_train[:10]}")
# show shapes of our dataset
print(f"shape of X_train: {X_train.shape}, shape of y_train: {y_train.shape}")


unique classes [0 1 2 3]
class representation [3 3 3 0 3 3 3 3 2 0]
shape of X_train: (100, 2), shape of y_train: (100,)
1
2
3
4
5
6
7
8
9
10
11

2.2 模型

将使用如图所示的2层网络。

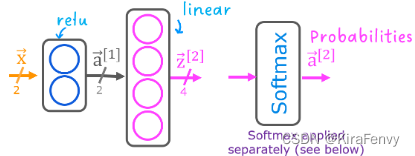
与二分类网络不同，该网络有四个输出，每类一个。给定一个输入示例，具有最大值的输出是输入的预测类。

下面是如何在Tensorflow中构建此网络的示例。请注意，输出层使用“linear”而不是“softmax”激活。虽然可以将softmax包含在输出层中，但如果在训练期间将linear输出传递给损失函数，则数值更稳定。如果模型用于预测概率，则可以在该点应用softmax。

tf.random.set_seed(1234)  # applied to achieve consistent results
model = Sequential(
    [
        Dense(2, activation = 'relu',   name = "L1"),
        Dense(4, activation = 'linear', name = "L2")
    ]
)
model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(0.01),
)

model.fit(
    X_train,y_train,
    epochs=200
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

数据可视化

def plt_mc_data(ax, X, y, classes,  class_labels=None, map=plt.cm.Paired, 
                legend=False, size=50, m='o', equal_xy = False):
    """ Plot multiclass data. Note, if equal_xy is True, setting ylim on the plot may not work """
    for i in range(classes):
        idx = np.where(y == i)
        col = len(idx[0])*[i]
        label = class_labels[i] if class_labels else "c{}".format(i)
        #ax.scatter(X[idx, 0], X[idx, 1],  marker=m,
        #            c=col, vmin=0, vmax=map.N, cmap=map,
        #            s=size, label=label)
        ax.scatter(X[idx, 0], X[idx, 1],  marker=m,
                    color=map(col), vmin=0, vmax=map.N, 
                    s=size, label=label)
    if legend: ax.legend()
    if equal_xy: ax.axis("equal")

plt_cat_mc(X_train, y_train, model, classes)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

上面的决策边界显示了模型如何划分输入空间。这个非常简单的模型对训练数据进行分类没有任何困难。它是如何做到这一点的？让我们更详细地了解一下网络。

下面，我们将从模型中提取经过训练的权重，并使用它来绘制每个网络单元的函数。更进一步，有一个更详细的结果解释。你不需要知道这些细节就可以成功地使用神经网络，但它可能有助于获得关于层如何结合来解决分类问题的更多直觉。

首先看看第一层relu过后产生了什么

# gather the trained parameters from the first layer
l1 = model.get_layer("L1")
W1,b1 = l1.get_weights()
1
2
3

def plt_layer_relu(X, Y, W1, b1, classes):
    nunits = (W1.shape[1])
    Y = Y.reshape(-1,)
    fig,ax = plt.subplots(1,W1.shape[1], figsize=(7,2.5))
    fig.canvas.toolbar_visible = False
    fig.canvas.header_visible = False
    fig.canvas.footer_visible = False

    for i in range(nunits):
        layerf= lambda x : np.maximum(0,(np.dot(x,W1[:,i]) + b1[i]))
        plt_prob_z(ax[i], layerf)
        plt_mc_data(ax[i], X, Y, classes, map=dkcolors_map,legend=True, size=50, m='o')
        ax[i].set_title(f"Layer 1 Unit {i}")
        ax[i].set_ylabel(r"$x_1$",size=10)
        ax[i].set_xlabel(r"$x_0$",size=10)
    fig.tight_layout()
    plt.show()
# plot the function of the first layer
plt_layer_relu(X_train, y_train.reshape(-1,), W1, b1, classes)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

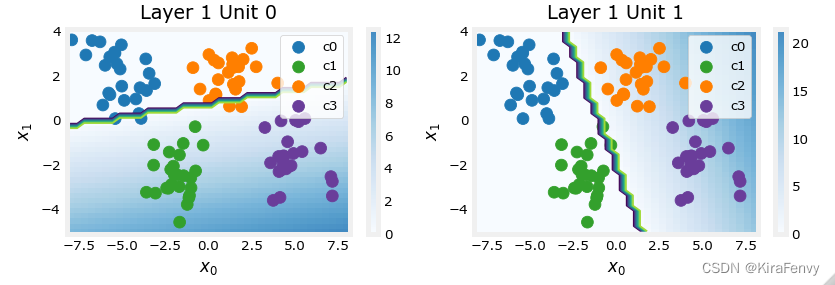
• 这些图显示了网络第一层中单元0和1的功能。轴上的输入为（$x_0，x_1$）。单元的输出由背景颜色表示。这由每个图形右侧的颜色条表示。注意，由于这些单元使用ReLu，输出不一定在0和1之间，在这种情况下，峰值大于20。
• 此图中的轮廓线显示输出$a_j^{[1]}$为零和非零之间的边界，这条线的白色那边都是0
• Unit 0将类0和1与类2和3分隔开。线左侧的点（类0和类1）将输出零，而右侧的点将输出大于零的值。
• Unit 1 将0级和2级与1级和3级分开。直线的上面的点（类0和2中）将输出零，而下面的点将输出大于零的值。
  

第二层之后发生了什么

# gather the trained parameters from the output layer
l2 = model.get_layer("L2")
W2, b2 = l2.get_weights()
# create the 'new features', the training examples after L1 transformation
Xl2 = np.zeros_like(X_train)
Xl2 = np.maximum(0, np.dot(X_train,W1) + b1)

plt_output_layer_linear(Xl2, y_train.reshape(-1,), W2, b2, classes,
                        x0_rng = (-0.25,np.amax(Xl2[:,0])), x1_rng = (-0.25,np.amax(Xl2[:,1])))
1
2
3
4
5
6
7
8
9

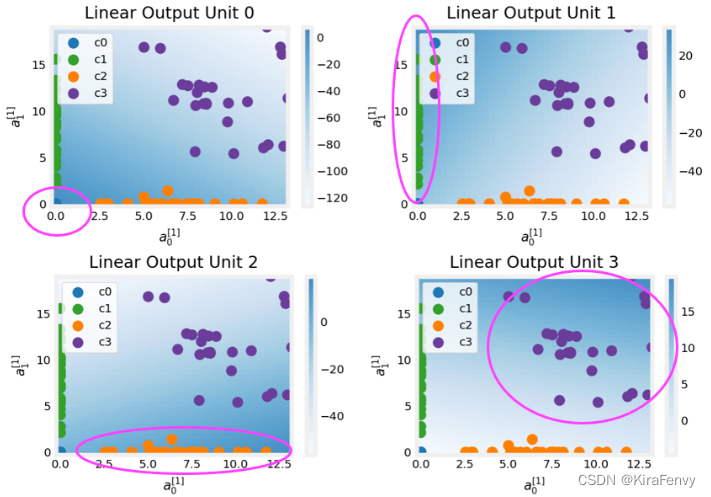
这些图中的点是第一层翻译的训练示例。一种方法是，第一层创建了一组新的功能，供第二层评估。这些绘图中的轴是前一层$a_0^{[1]}$和$a_1^{[1]}$的输出。如上所述，类0和1（绿色和蓝色）有$a_0^{[1]}=0$，而类1和2（蓝色和绿色）有$a_1^{[1]}=0$。

同样，背景色的强度表示最高值。

Unit0将为接近（0,0）的值生成其最大值，其中类0（蓝色）已映射。

Unit1在左上角产生最高值，选择class 1（绿色）。

Unit2的目标是3级（橙色）所在的右下角。

Unit3在右上角产生最高值，选择我们的最后一个类（紫色）。

图中不明显的另一个方面是，各单位之间的值已经协调。一个单位仅为它所选择的类别产生最大值是不够的，它还必须是该类别中所有units的最高值。这是通过作为损失函数（SparseCategoricalCrossEntropy）一部分的隐含softmax函数实现的。与其他激活功能不同，softmax适用于所有输出。

你可以成功地使用神经网络，而不需要知道每个unit的详细情况。希望这个例子能够提供一些帮助