python数学建模--线性规划问题案例及求解

本博客参考：

1. 《python数学实验与建模》
2. 《MATLAB数学建模经典案例实战》

数学问题：线性规划问题

m a x   z = 8 x 1 − 2 x 2 + 3 x 3 − x 4 − 2 x 5 { x 1 + x 2 + x 3 + x 4 + x 5 ≤ 400 x 1 + 2 x 2 + 2 x 3 + x 4 + 6 x 5 ≤ 800 2 x 1 + x 2 + 6 x 3 ≤ 200 x 3 + x 4 + 5 5 ≤ 200 0 ≤ x i ≤ 99 , i = 1 , 2 , 3 , 4 x 5 ≥ − 10 max \ z=8x_1-2x_2+3x_3-x_4-2x_5\\ \left\{

\right. max z=8x1​−2x2​+3x3​−x4​−2x5​⎩ ⎨ ⎧​​x1​+x2​+x3​+x4​+x5​≤400x1​+2x2​+2x3​+x4​+6x5​≤8002x1​+x2​+6x3​≤200x3​+x4​+55​≤2000≤xi​≤99,i=1,2,3,4x5​≥−10​

程序设计

from scipy.optimize import linprog

c=[-8,2,-3,1,2]
A=[[1,1,1,1,1],[1,2,2,1,6],[2,1,6,0,0],[0,0,1,1,5]]
b=[[400],[800],[200],[200]]
aeq=None
beq=None
bounds=((0, 99),(0, 99),(0, 99),(0, 99),(-10,None))
res=linprog(c=c, A_ub=A, b_ub=b, A_eq=aeq, b_eq=beq, bounds=bounds,)
1
2
3
4
5
6
7
8
9

运行结果

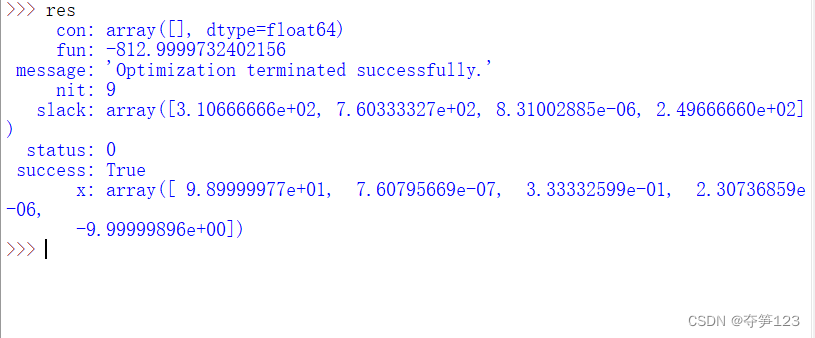
结果分析

从中我们看出，目标函数z的最大值应为823左右，此时决策变量$x_1-x_5$的值分别为[99,0,0.3,0,-10]

实际应用1：加工厂的生产计划

一家加工厂使用牛奶生产A,B两种奶制品，1桶牛奶经甲机器加工12小时得到3kgA，也可以经过乙机器8小时得到4kgB，根据市场需求，生产的A、B可以全部出售并且每kgA获利24元、每kgB获利16元。现在该工厂每天获得50桶牛奶供应，所有工人的最大劳动时间之和为480x小时，甲机器每天最多加工100kgA，乙机器加工不限量，请你为该工厂设计生产计划，使得每天的利润最大

设置未知数

假设每天用于生产A产品的牛奶为$x_1$桶，用于生产B产品的牛奶为$x_2$桶，每天的利润为$z$元，根据题意建立数学模型

建立数学模型

m a x   z = 3 ∗ 24 x 1 + 4 ∗ 16 x 2 { x 1 + x 2 ≤ 50 12 x 1 + 8 x 2 ≤ 800 3 x 1 ≤ 100 x 1 ≥ 0 , x 2 ≥ 0 max \ z=3*24x_1+4*16x_2\\ \left\{

\right. max z=3∗24x1​+4∗16x2​⎩ ⎨ ⎧​x1​+x2​≤5012x1​+8x2​≤8003x1​≤100x1​≥0,x2​≥0​
转化为标准形式
m i n   z = − 3 ∗ 24 x 1 − 4 ∗ 16 x 2 { x 1 + x 2 ≤ 50 12 x 1 + 8 x 2 ≤ 800 3 x 1 ≤ 100 x 1 ≥ 0 , x 2 ≥ 0 min \ z=-3*24x_1-4*16x_2\\ \left\{

x1+x2≤5012x1+8x2≤8003x1≤100x1≥0,x2≥0" role="presentation">x1+x2≤5012x1+8x2≤8003x1≤100x1≥0,x2≥0$$\begin{array}{r}{x}_1+x_2\le 50\\ 12x_1+8x_2\le 800\\ 3x_1\le 100\\ x_1\ge 0,x_2\ge 0\end{array}$$

\right. min z=−3∗24x1​−4∗16x2​⎩ ⎨ ⎧​x1​+x2​≤5012x1​+8x2​≤8003x1​≤100x1​≥0,x2​≥0​

程序设计

from scipy.optimize import linprog
c=[-72,-64]
A=[[1,1],[12,8]]
b=[[50],[480]]
bounds=((0,100/3.0),(0,None))

res=linprog(c=c, A_ub=A, b_ub=b, A_eq=None, b_eq=None, bounds=bounds) 
1
2
3
4
5
6
7

运行结果

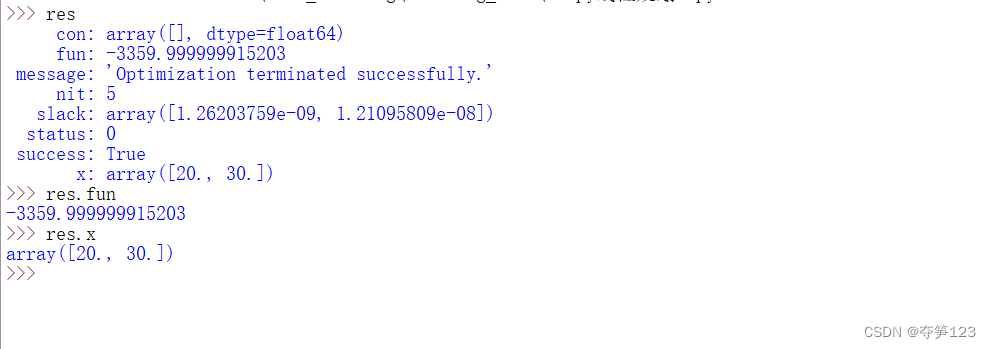
结果分析

从上面我们可以看出，利润最大值在3360元左右，达到最大值时，A、B产品的牛奶日用量分别是20桶、30桶

实际应用2：油料加工厂的采购和加工计划

某加工厂加工一种油，原料为五种油（植物油1，植物油2、非植物油1，非植物油2、非植物油3），每种油的价格、硬度如图表所示，最终生产的成品将以150英镑/吨

每个月能够提炼的植物油不超过200吨、非植物油不超过250吨，假设提炼过程中油料没有损失，提炼费用忽略不计，并且最终的产品的硬度需要在（3-6）之间（假设硬度的混合时线性的）。根据以上信息，请你为加工厂指定月采购和加工计划

设置未知数

假设$x_1,x_2,x_3,x_4,x_5$分别为每月需要采购的原料油吨数，$x_6$为每个月加工的成品油吨数，根据题意建立数学模型

建立数学模型

m a x   z = − 110 x 1 − 120 x 2 − 130 x 3 − 110 x 4 − 115 x 5 + 150 x 6 { x 1 + x 2 ≤ 200 x 3 + x 4 + x 5 ≤ 250 8.8 x 1 + 6.1 x 2 + 2.0 x 3 + 4.2 x 4 + 5.0 x 5 ≤ 6 x 6 8.8 x 1 + 6.1 x 2 + 2.0 x 3 + 4.2 x 4 + 5.0 x 5 ≥ 3 x 6 x 1 + x 2 + x 3 + x 4 + x 5 = x 6 x i ≥ 0 , i = 1 , 2 , 3 , . . . , 6 max \ z=-110x_1-120x_2-130x_3-110x_4-115x_5+150x_6\\ \left\{

\right. max z=−110x1​−120x2​−130x3​−110x4​−115x5​+150x6​⎩ ⎨ ⎧​x1​+x2​≤200x3​+x4​+x5​≤2508.8x1​+6.1x2​+2.0x3​+4.2x4​+5.0x5​≤6x6​8.8x1​+6.1x2​+2.0x3​+4.2x4​+5.0x5​≥3x6​x1​+x2​+x3​+x4​+x5​=x6​xi​≥0,i=1,2,3,...,6​

程序设计

from scipy.optimize import linprog

c=[110,120,130,110,115,-150]
A=[[1,1,0,0,0,0],[0,0,1,1,1,0],[8.8,6.1,2.0,4.2,5.0,-6],[-8.8,-6.1,-2.0,-4.2,-5.0,3]]
b=[[200],[250],[0],[0]]
aeq=[[1,1,1,1,1,-1]]
beq=[[0]]
bounds=((0, None),(0, None),(0, None),(0, None),(0,None),(0,450))
# bounds=((0, None),(0, None),(0, None),(0, None),(0,None),(0,None))
res=linprog(c=c, A_ub=A, b_ub=b, A_eq=aeq, b_eq=beq, bounds=bounds)
1
2
3
4
5
6
7
8
9
10

运行结果

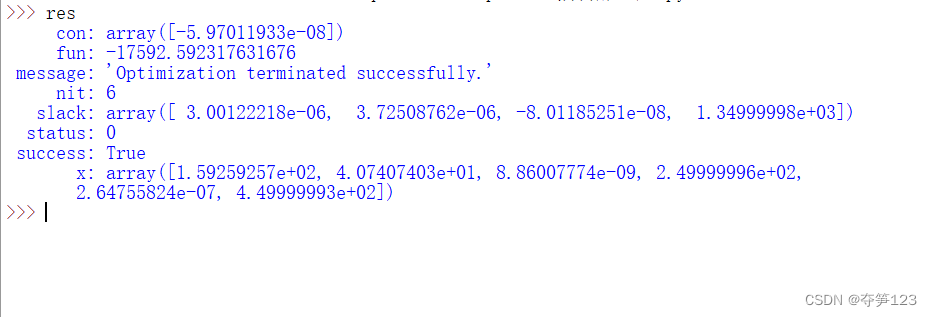
结果分析

从上面我们可以看到，五种原料油的采购量分别为[159.25,40.7407,0,250,0]（吨），此时总利润可以达到最大，约为17592英镑/月

笔者发现的一个没有用的小技巧：我们知道$x_6$变量代表的是每个月的吨数，bounds参数设置决策变量的取值区间，当在bounds中对x_6的上界不加限制时，即（0,None）,模型返回的结果中仍然将$x_6$收敛至450，你知道这是为什么吗？

遗留的问题

经过这么多的应用，我们已经大致明白了scipy.optimize.linprog()函数的使用过程，也惊叹于它的便利之处，但是不知道你是否能发现该函数的缺点？
我们来看下面一个问题

钢管加工用料问题

某零售商从钢管厂进货后将钢管切割后卖给客户，某次进货该零售商得到了若干1850mm长的原料钢管。现有一客户需要15根290mm、28根315mm、21根350mm、30根455mm的钢管。对于一个原料钢管有四种切割模式，每次切割模式下的切割次数不能太多（一根原料钢管最多生产5根产品），为减少余料浪费，每种切割模式下的余料浪费不能超过100mm。（要完成该客户的需求，需要若干根原料钢管，可能用到四种切割模式，现规定使用频率最多的切割模式按照一根原料钢管价格的1/10收取加工费，使用频率次之的切割模式按照一根原料钢管价格的2/10收取加工费，依次类推）。现在求使得该零售商总费用最小的切割计划？

分析

仔细分析我们会发现，这个问题的线性规划和上面的两个实际问题有很大不同。

在上面的问题中，决策变量只有一种$x_1-x_n$，而且决策变量的系数的都是常数（比如$x_3+x_4+x_5\le 250$中的每个自变量系数都是1）。但是在该问题中似乎有两种决策变量：切割模式的使用频次$x_i$、每种切割模式下对于一根原料钢管产生的成品钢管种类及数量$r_{ij}$（i表示第i种切割模式，j表示第j种成品钢管）。

scipy.optimize.linprog()的缺陷？

这就让我们在列举约束条件时遇到了很大的困难，比如其中一个不等式是这样的${\sum }_{i=1}^4{x}_i\times r_{1i}\ge 15(i=\mathrm{1...4})$，看到这里我们发现两个决策变量相乘，如果继续使用scipy.optimize.linprog()函数，参数A_ub怎么取？参数bounds到底该以谁作为决策变量？

现在我们似乎遇到了困难，实际上并不是linprog()函数的问题，因为函数就是用来求解线性规划问题的，而我们现在提出的这个问题是一个非线性规划问题，所以，要解决它我们需要“另辟蹊径”了！下一个博客我们将用另外一个第三方库解决这个问题