机器学习之集成学习

一、集成学习基本介绍

Ensemble Learning

集成学习本身不是一个单独的机器学习算法，而是通过构建并结合多个机器学习器来完成学习任务。

---

二、集成学习算法及sklearn实现

1. Voting Classifier

（1）Hard Voting Classifier

投票：少数服从多数

from sklearn import datasets

X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)

from sklearn.model_selection import train_test_split  # 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

from sklearn.ensemble import VotingClassifier

voting_clf = VotingClassifier(estimators=[   # estimators估计器
    ('log_clf', LogisticRegression()),      # 第一个模型 逻辑回归分类器
    ('svm_clf', SVC()),                     # 第二个模型 SVM分类器
    ('dt_clf', DecisionTreeClassifier())    # 第三个模型 决策树
], voting='hard')   # voting='hard',少数服从多数

voting_clf.fit(X_train, y_train)
print(voting_clf.score(X_test, y_test))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

（2）Soft Voting Classifier

更合理的投票，应该具有权值。要求集合中的每个模型都能估计概率，例如逻辑回归、KNN等，SVM中的SVC分类器也可以通过设置参数probability=True计算概率。

voting_clf2 = VotingClassifier(estimators=[   # estimators估计器
    ('log_clf', LogisticRegression()),                      # 第一个模型 逻辑回归分类器
    ('svm_clf', SVC(probability=True)),                     # 第二个模型 SVM分类器 设置probability=True
    ('dt_clf', DecisionTreeClassifier(random_state=666))    # 第三个模型 决策树
], voting='soft')   # voting='hard',少数服从多数

voting_clf2.fit(X_train, y_train)
print(voting_clf2.score(X_test, y_test))

1
2
3
4
5
6
7
8
9

---

2. Bagging和Pasting

虽然有很多的机器学习算法，但是从投票的角度看，仍然不够多，如果有成千上万的投票者，才能保证最终结果可信（大数定律）。

所以需要创建更多的子模型，并且子模型之间要有差异性，不能保持一致。

每个子模型不需要太高的准确率

1. Bagging(放回取样-更常用)

• 从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）
• 每次使用一个训练集得到一个模型，k个训练集共得到k个模型。
• 对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=500,       # n_estimators:要集成几个决策树模型
                                max_samples=100,        # max_samples:每个子模型要看多少个样本数据
                                bootstrap=True)         # bootstrap:放回取样/不放回取样 若False即Pasting

bagging_clf.fit(X_train, y_train)
print(bagging_clf.score(X_test, y_test))
1
2
3
4
5
6
7
8
9
10

理论上讲，若n_estimators升为5000越大，准确率更高

1.1 使用OOB

OOB(Out-of-Bags)，放回取样会导致平均有37%的样本没有取到。我们可以转而不使用测试集，而使用这部分没有取到的样本做测试。

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=500,       # n_estimators:要集成几个决策树模型
                                max_samples=100,        # max_samples:每个子模型要看多少个样本数据
                                bootstrap=True,         # bootstrap:放回取样/不放回取样 若False即Pasting
                                oob_score=True)         # 放回取样过程中，记录取了哪些

bagging_clf.fit(X, y)   # 传入所有的数据
print(bagging_clf.oob_score_)   # oob_score_属性
1
2
3
4
5
6
7
8
9
10
11

还可以设置参数n_jobs=-1进行并行处理。

1.2 Random Subspaces

针对特征进行随机取样，不针对样本进行随机取样

random_subspaces_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=500, max_samples=500,        # max_samples和n_estimators相等，即不针对样本取样
                                bootstrap=True, oob_score=True,              # max_features:每次看多少个特征
                                max_features=1, bootstrap_features=True)     # bootstrap_features: 对特征放回取样
                                
random_subspaces_clf.fit(X, y) 
random_subspaces_clf.oob_score_
1
2
3
4
5
6
7

1.3 Random Patches

既针对样本，又针对特征进行随机取样

random_patches_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=500, max_samples=100,        # max_samples和n_estimators不相等，即针对样本取样
                                bootstrap=True, oob_score=True,              # max_features:每次看多少个特征
                                max_features=1, bootstrap_features=True)     # bootstrap_features: 对特征放回取样
                                
random_patches_clf.fit(X, y) 
random_patches_clf.oob_score_
1
2
3
4
5
6
7

---

2. 随机森林（Bagging+决策树）

sklearn实现思路：决策树在节点划分时，在随机的特征子集上寻找最优划分特征

from sklearn.ensemble import RandomForestClassifier

rf_clf = RandomForestClassifier(n_estimators=500, random_state=666, oob_score=True)

rf_clf.fit(X, y)
rf_clf.oob_score_
1
2
3
4
5
6

RandomForestClassifier()有很多参数可以调节，例如max_leaf_nodes每棵决策树最多有多少个叶子结点。

若在决策树节点划分时，使用随机的特征和随机的阈值，就变成了Extra-Tree ——提供了额外的随机性，抑制了过拟合，但增大了bias（增大偏差，遏制方差）

from sklearn.ensemble import ExtraTreesClassifier

et_clf = ExtraTreesClassifier(n_estimators=500, bootstrap=True, oob_score=True, random_state=666)

et_clf.fit(X, y)
et_clf.oob_score_
1
2
3
4
5
6

---

3. Boosting

• 每一轮的训练数据样本赋予一个权重，并且每一轮样本的权值分布依赖上一轮的分类结果。
• 基分类器之间采用序列式的线性加权方式进行组合。

1. Ada Boosting

之前分类错的样本会被赋予更高的权重

from sklearn import datasets

X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)

from sklearn.model_selection import train_test_split  # 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier  # Base estimator

ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=500)
ada_clf.fit(X_train, y_train)
print(ada_clf.score(X_test, y_test))

1
2
3
4
5
6
7
8
9
10
11
12
13
14

2. Gradient Boosting

训练一个模型m1，产生错误e1
针对e1训练第二个模型m2，产生错误e2
针对e2训练第三个模型m3，产生错误e3…
最终预测结果是：m1 + m2 + m3 + …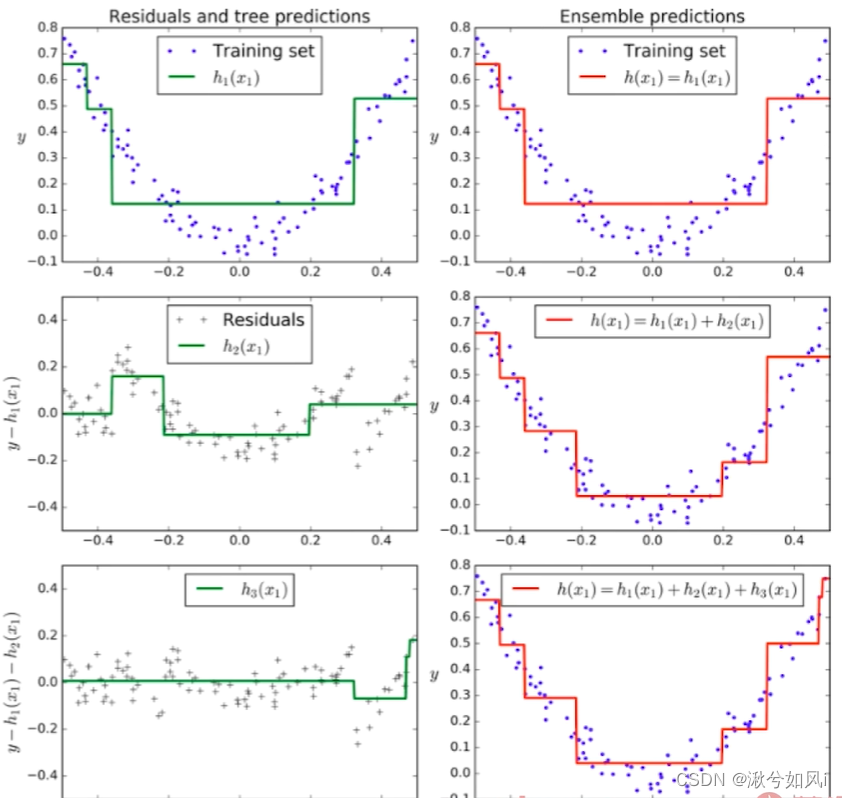

from sklearn.ensemble import GradientBoostingClassifier

gb_clf = GradientBoostingClassifier(max_depth=2, n_estimators=30)

gb_clf.fit(X_train, y_train)
gb_clf.score(X_test, y_test)

1
2
3
4
5
6
7

---

4. Stacking

将训练集分为两份，首先使用第一份训练集subset1，把底下3个模型训练好。然后用我们训练出的这 3 个模型，对 subset2 数据集中的每一个数据进行预测。这样，对于 subset2 数据集中的每一条数据，我们都产生了 3 个结果。同时，subset2 数据集是包含 y 值（真值）的。将这3个结果也就是3个新特征和subset2的y值结合，形成新的数据集，再用来训练上层模型。

新的数据集的特征数量，和原先数据集的特征数量无关，而是和 stacking 中第一层集合了多少学习算法相关！

---

总结

优缺点

1. 优点

• 提高预测性能，直接级联不同模型，容易实现，参数较少

2. 缺点

• 多个模型混合在一起是预测结果不可理解，黑盒系统

Bagging和Boosting区别

1. 样本选择上：

   • Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。
   • Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2. 样例权重：

   • Bagging：使用均匀取样，每个样例的权重相等。
   • Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3. 预测函数：

   • Bagging：所有预测函数的权重相等。
   • Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4. 并行计算：

   • Bagging：各个预测函数可以并行生成。
   • Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

问题

1. 待完善