C++11之追踪返回类型

系列文章

C++11之正则表达式（regex_match、regex_search、regex_replace）

C++11之线程库（Thread、Mutex、atomic、lock_guard、同步）

C++11之智能指针（unique_ptr、shared_ptr、weak_ptr、auto_ptr）浅谈内存管理

C++11之强制类型转换（static_cast,const_cast,dynamic_cast,reinterpret_cast）

C++11之Lanbda表达式(匿名函数)

C++11之右值引用：移动语义和完美转发(带你了解移动构造函数、纯右值、将亡值、右值引用、std::move、forward等新概念)

C++11之委派构造函数

C++11之内联名字空间（inline namespace）和ADL特性(Argument-Dependent name Lookup)

C++11之模板的别名

C++11之一般化的SFINAE规则

C++11之auto类型推导

C++11之decltype类型推导（使用场景、推导四规则、cv限定符）

---

---

追踪返回类型

追踪返回类型的引入

前面我们讲了auto和decltype在泛式编程中的作用，今天我们在学一个能够让auto和decltype在泛式编程中更加强大的----追踪返回类型

在函数模板中，函数的类型取决于参数的类型，那么当参数类型是动态时，返回类型也是动态的。
下面我以俩数相加函数为例：

template<typename T1, typename T2>
decltype(t1 + t2) Sum(T1& t1, T2& t2)
{
	return t1 + t2;
}
1
2
3
4
5

输入的类型不确定 返回的类型不确定
就会写出下面这种返回类型。由于C++编译器是从左往右顺序读入的，按照变量需要先声明后使用的规则，所以这种写法注定是不会编译器允许的。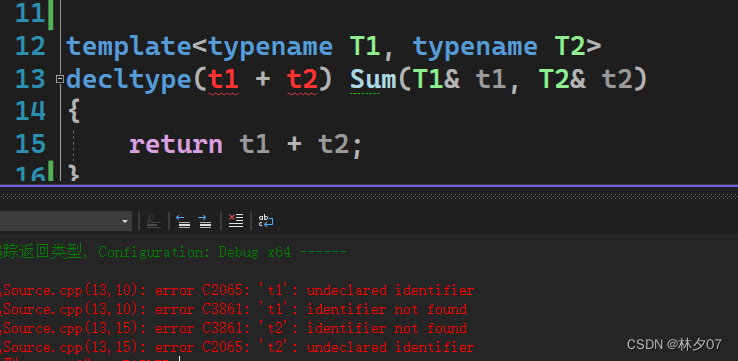

为了满足C/C++编译器的规则，所以我们可以将计算得到的结果从返回值的形式转为出参。

template<typename T1, typename T2>
void Sum(T1& t1, T2& t2, decltype(t1 + t2)& ret)
{
	ret = t1 + t2;
}
1
2
3
4
5

这样的写法的确满足了编译器的规则，但是在使用方上并没有提高便捷性，因为这种的函数模板需要在使用时就需要确定出参类型，因为要先定义。

int main()
{
	int i = 9;
	double j = 3.3;

	double s = 0;
	Sum(i, j, s);
	cout << s << endl;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11

使用追踪返回类型的函数

上述的解决方案都并不是那么的完美，为此C++11引入了新语法 追踪返回类型，类似于lanbda的表达式中的返回类型的写法。
追踪返回类型：将函数的返回类型移到函数最后部分，格式：->返回类型 原本返回类型的位置将会由auto去占位。这样完美就可以让编译器来推导Sum函数模板的返回类型了。auto占位符 与
->return_type 就构成了追踪返回类型函数的俩个基本必备要素。

下面就是使用追踪返回类型的方法实现的俩数相加的函数

template<typename T1, typename T2>
auto Sum(T1& t1, T2& t2)->decltype(t1 + t2)
{
	return 0;
}
1
2
3
4
5

常规/普通函数中也可以使用追踪返回类型

这种追踪返回类型不仅仅局限于上述的场景，在常规/普通函数中也可以使用。

int TestFunction1(int i)
{
	return i * 2;
}

auto TestFunction2(int i)->int
{
	return i * 2;
}
1
2
3
4
5
6
7
8
9

返回类型如果和函数的作用域相同或者被包含时则返回类型处可以省略作用域

令人糟糕的是，上述的例子在写法上复杂了，而且易读性也降低了。但它也有好处，返回类型如果和函数的作用域相同或者被包含时则返回类型处可以省略作用域。

下面我创建了一个OuterType类，还有一个成员函数，其中这个函数返回类型的作用域也是在OuterType类内，所以返回类型的作用域就可以省略掉。

class OuterType
{
public:
	struct InnerType
	{
		int i;
	};

	InnerType GetInner();
	InnerType it;
};

auto OuterType::GetInner()->/*OuterType::*/InnerType
{
	return it;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

C++11引追踪返回类型后，对于模板编程中的类型推导也提高了一个台阶，让泛式编程更加强大 直观的看代码，有种python的感觉，模板函数中没有一个具体的类型。而对于模板的设计者提供了极高的便捷性，编写上也极大的简化了代码的体积。

下面实现了俩数相加、俩数相乘的函数，均采用追踪返回类型的方式。那么在调用者使用的过程中是非常的便捷。

#include 

using namespace std;

template<typename T1, typename T2>
auto Sum(const T1& t1, const T2& t2)->decltype(t1 + t2)
{
	return t1 + t2;
}

template<typename T1, typename T2>
auto Mul(const T1& t1, const T2& t2)->decltype(t1 * t2)
{
	return t1 * t2;
}

int main()
{
	auto a = 3;
	auto b = 4LL;
	auto pi = 3.14;

	auto c = Mul(Sum(a, b), pi);

	cout << c << endl;

	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

在处理函数简化问题上,追踪返回类型也是一把好手

下面定义了令人头疼的pf函数，我们可以使用追踪返回类型很容易的将其简化。而且我们还可以通过is_same模板类来测试俩个函数是否相同。

#include 
#include 
using namespace std;


int (*(*pf())())()
{
	return nullptr;
}

/*
 * auto (*)() -> int(*)()  一个返回函数指针的函数 该函数没有参数，返回值类型为int  设这个函数为x
 * auto pf1() ->auto (*)() -> int(*)()  一个返回a函数指针的函数
 */
auto pf1() ->auto(*)()->int(*)()
{
	return nullptr;
}

int main()
{
	cout << boolalpha << is_same<decltype(pf), decltype(pf1)>::value << endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

参数与返回值类型不同时的转发

追踪返回类型的强大远不止于此，在模板函数中加入追踪返回类型可以实现参数与返回值类型不同时的转发。

在下面的代码中，我们实现了int转double和double转int的同名函数，还实现了一个Forward转发函数，其返回类型是通过fool(参数)的方式进行确定的。这样就可以根据输入的类型动态的变化返回的类型。

#include 

using namespace std;

double foo(int a)
{
	return static_cast<double>(a) + 0.1;
}

int foo(double d)
{
	return static_cast<int>(d);
}

template<class T>
auto Forward(T t)->decltype(foo(t))
{
	return foo(t);
}

int main()
{
	cout << Forward(1.2) << endl;
	cout << Forward(2) << endl;

	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

还可以广泛应用于函数指针、普通函数、函数应用等等中。没有返回类型的函数也可以被声明为追踪返回类型，只需要将最后的return_type写为void即可。