-
微分中值定理—罗尔中值定理
我们所说的微分中值定理,一般指三大微分中值定理。它包含
-
以米歇尔·罗尔的名字命名的--罗尔中值定理
-
以约瑟夫·路易·拉格朗日的名字命名的--拉格朗日中值定理
-
以及以奥古斯丁-路易·柯西的名字命名的--柯西中值定理

其中罗尔中值定理是基础,拉格朗日中值定理是罗尔中值定理的推广,柯西中值定理,是拉格朗日中值定理的推广。那么它们到底在讲什么呢?这节课,我们就来学习它们中的第一个,罗尔中值定理。
1 定义
定理(罗尔中值定理). 如果函数
满足:
那么
,使得
。
若
是这样一个函数,在
内闭区间连续,开区间可导。则,在
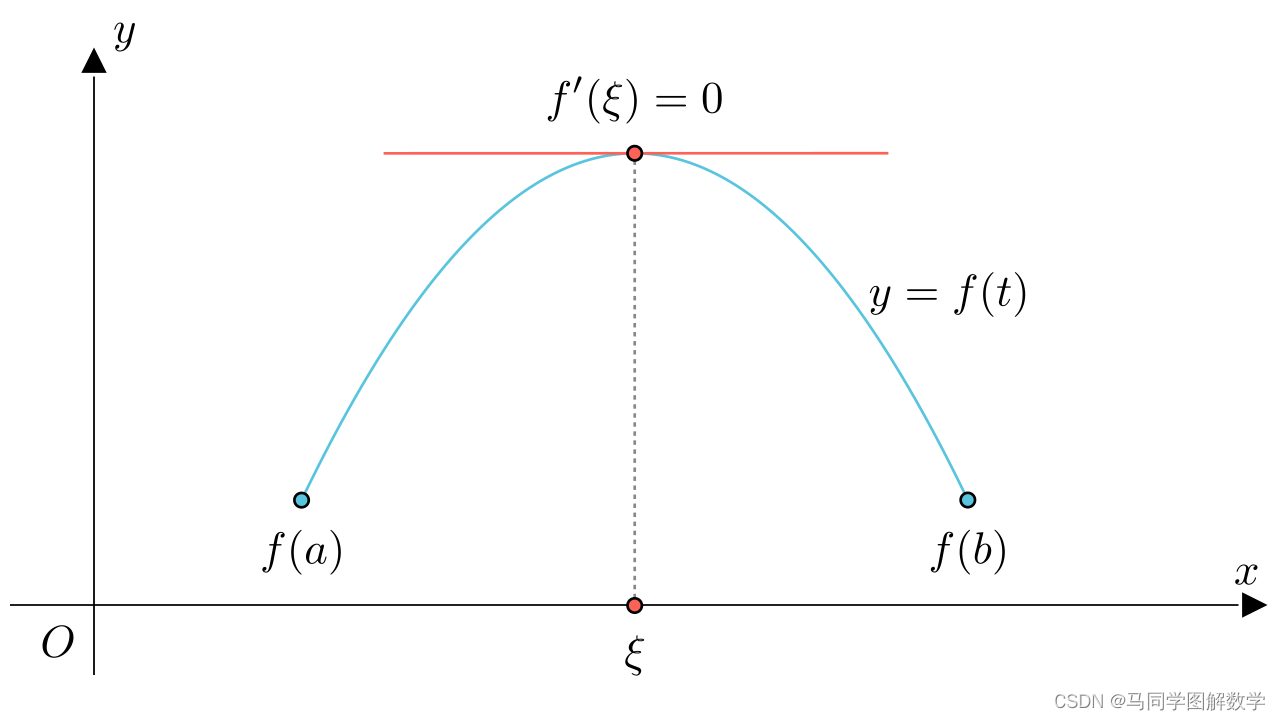
区间内,至少存在一个导数为零的点。而我们知道,导数就是切线的斜率。斜率为零,意味着是水平的。那么存在一个导数为零的点,从几何上看,就是存在一个点,这个点的切线是水平的。
2 往返跑
对于折返跑,相信大家并不陌生,它的最大特点是,起点和终点在同一个位置。

下面,我们以时间为横坐标,位移为纵坐标建立坐标系。假设开始的时刻为
,此时的位移为
。

当跑到最远位置的时候,位移最大,也就是函数值来到了最高点。
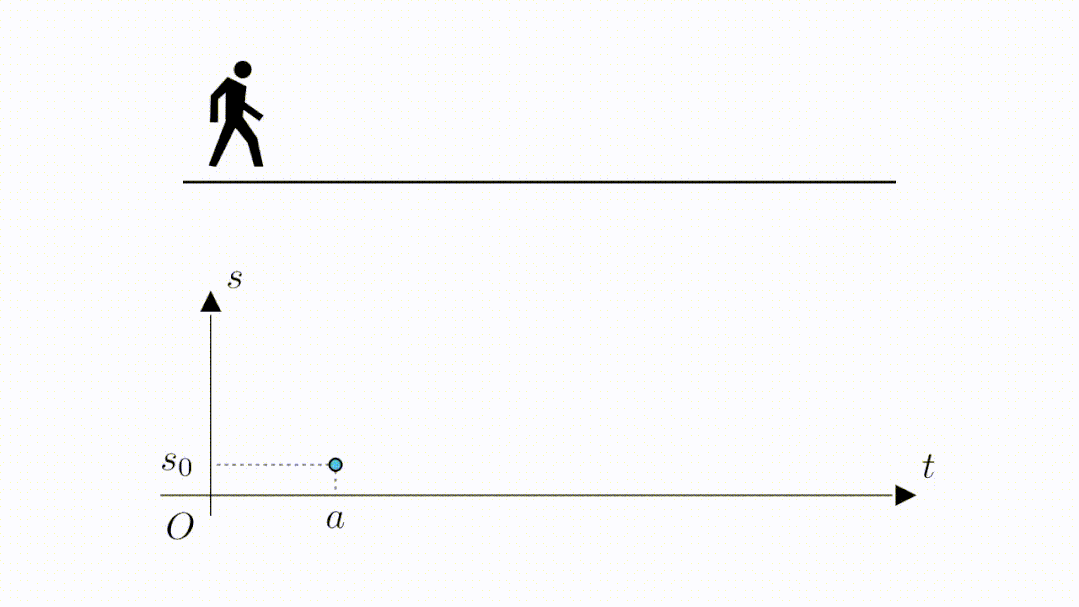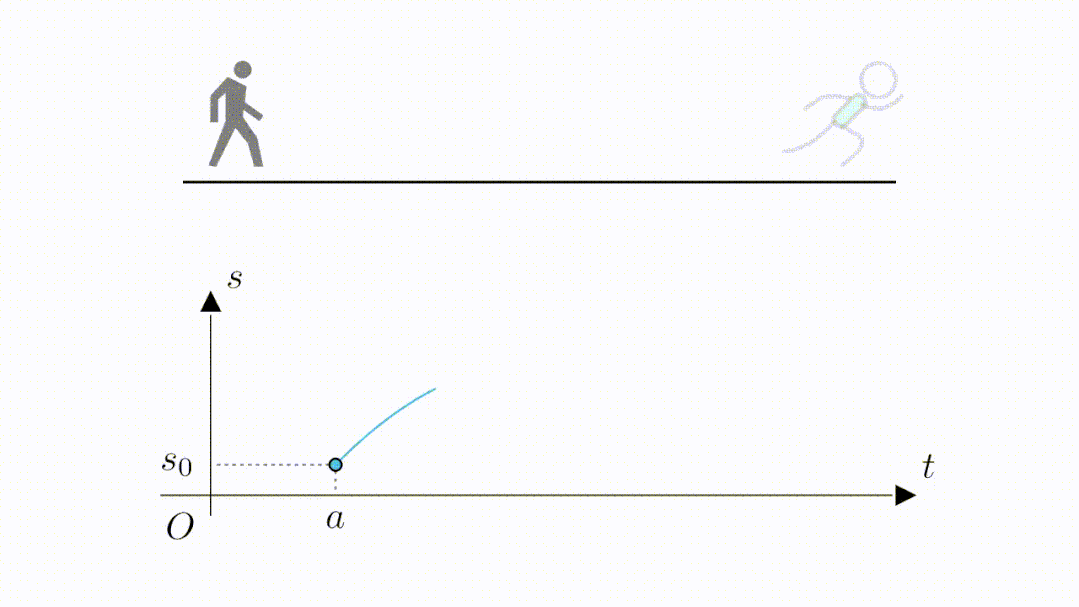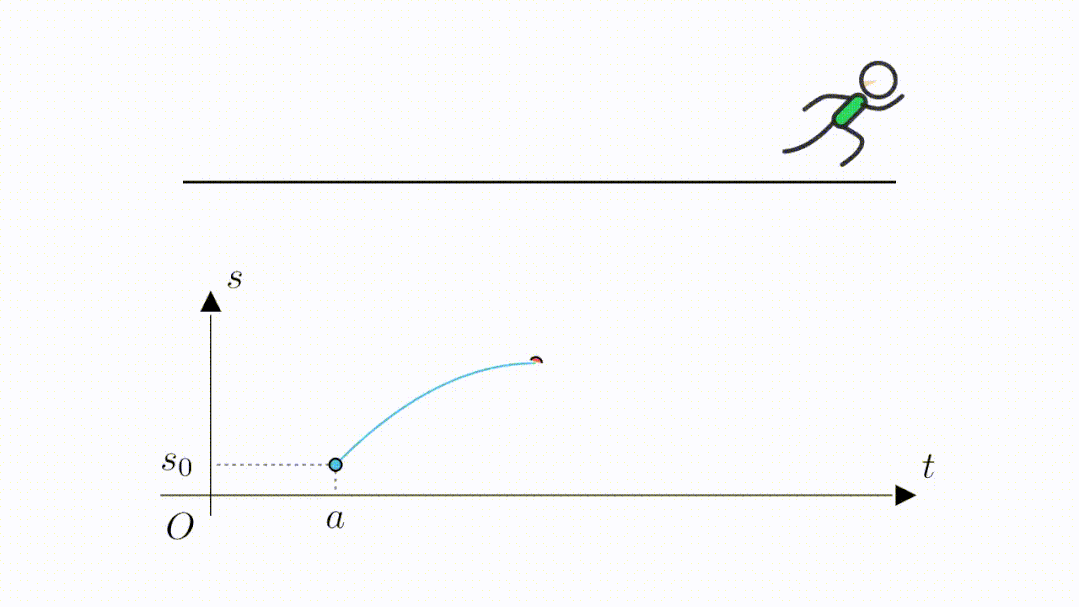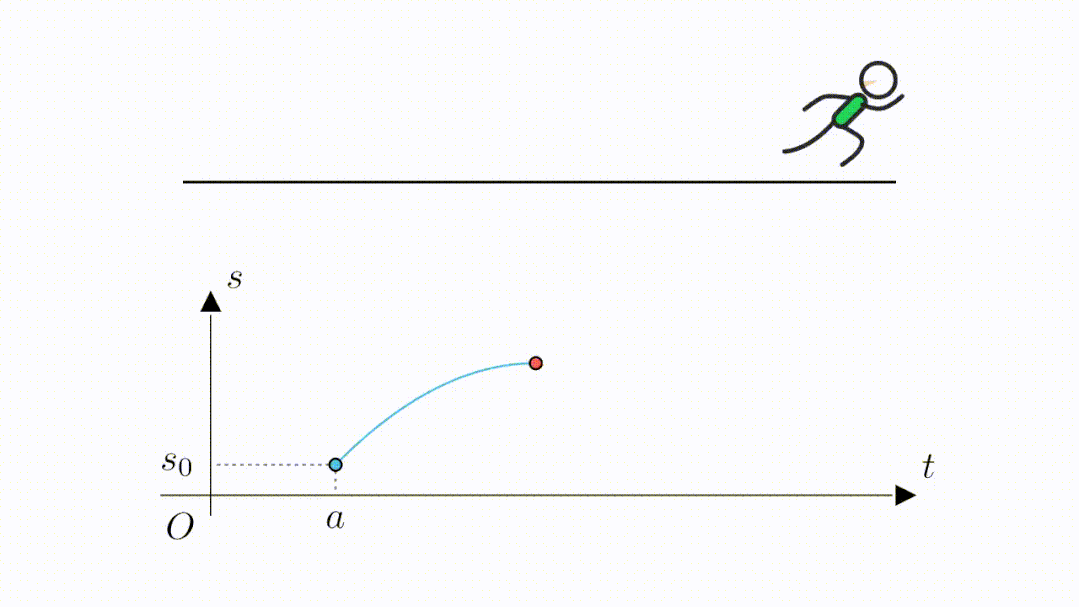
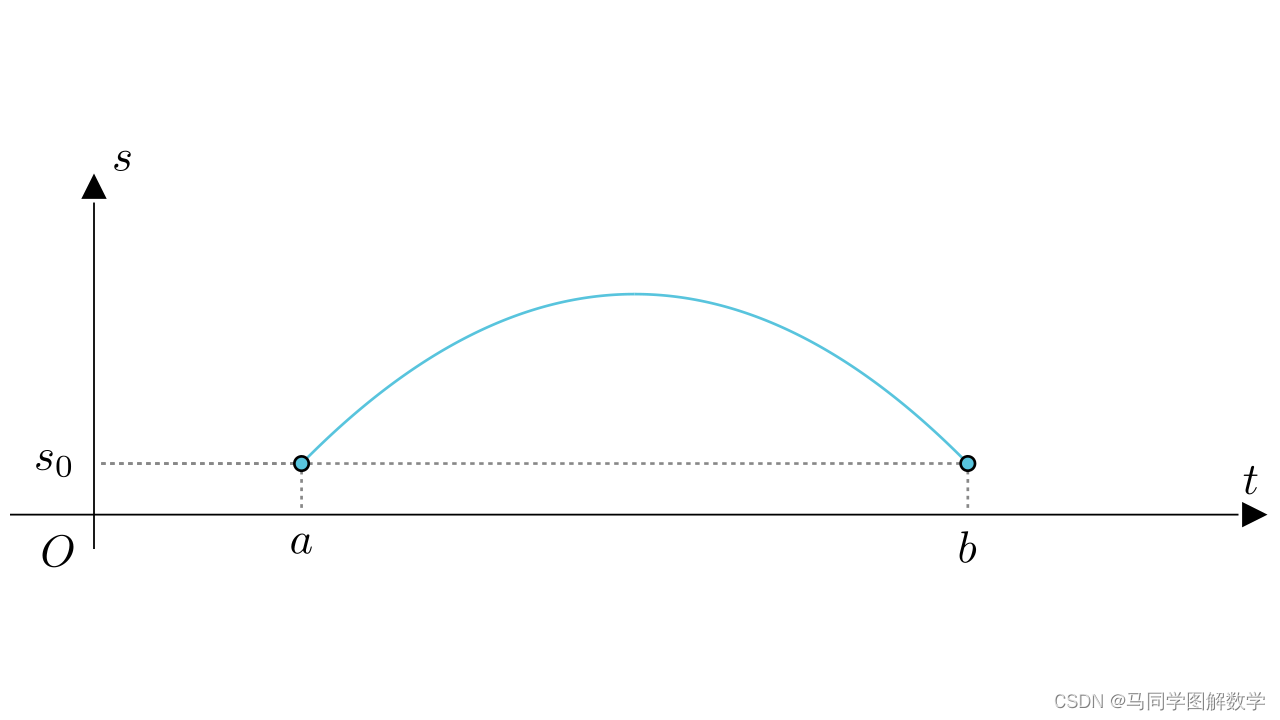
接着开始折返往回跑,函数值也就开始回落,当最后回到起点位置时,又来到了位移为
的位置。

可以看到,此时这个时间位移函数,在
内,闭区间连续,开区间可导,且在起点时刻(
),与终点时刻(
),的函数值(
)是相同的,也就是说,这个时间位移函数,是符合罗尔中值定理的条件的。
那么按照定理的描述,就应该有个点导数为零,哪个点呢---最高这个点。
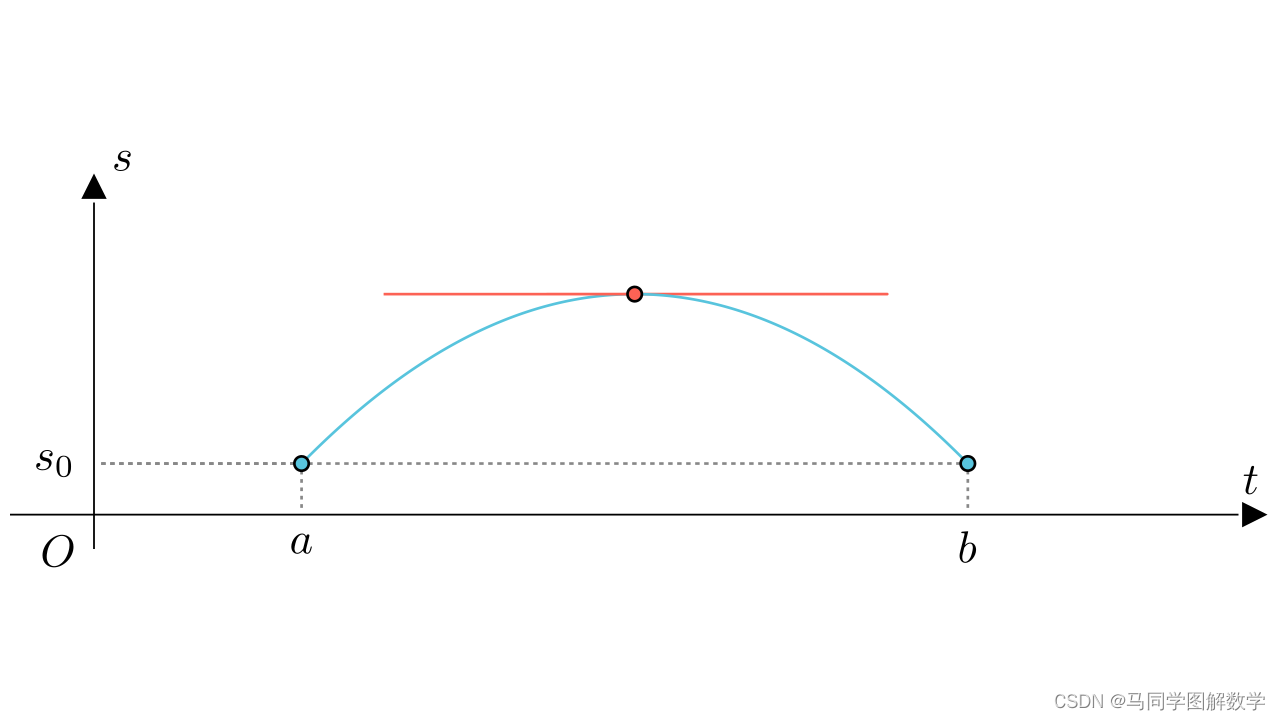
因为纵坐标为位移,那么最高这个点,其实就是距离起点最远的这个位置,此时折返跑要完成转向,因此必然出现一个速度为零的时刻。

而我们知道,瞬时速度就是位移相对于时间的导数,假设我们在
这个时间点,速度为零,那么过
点的切线就是水平的
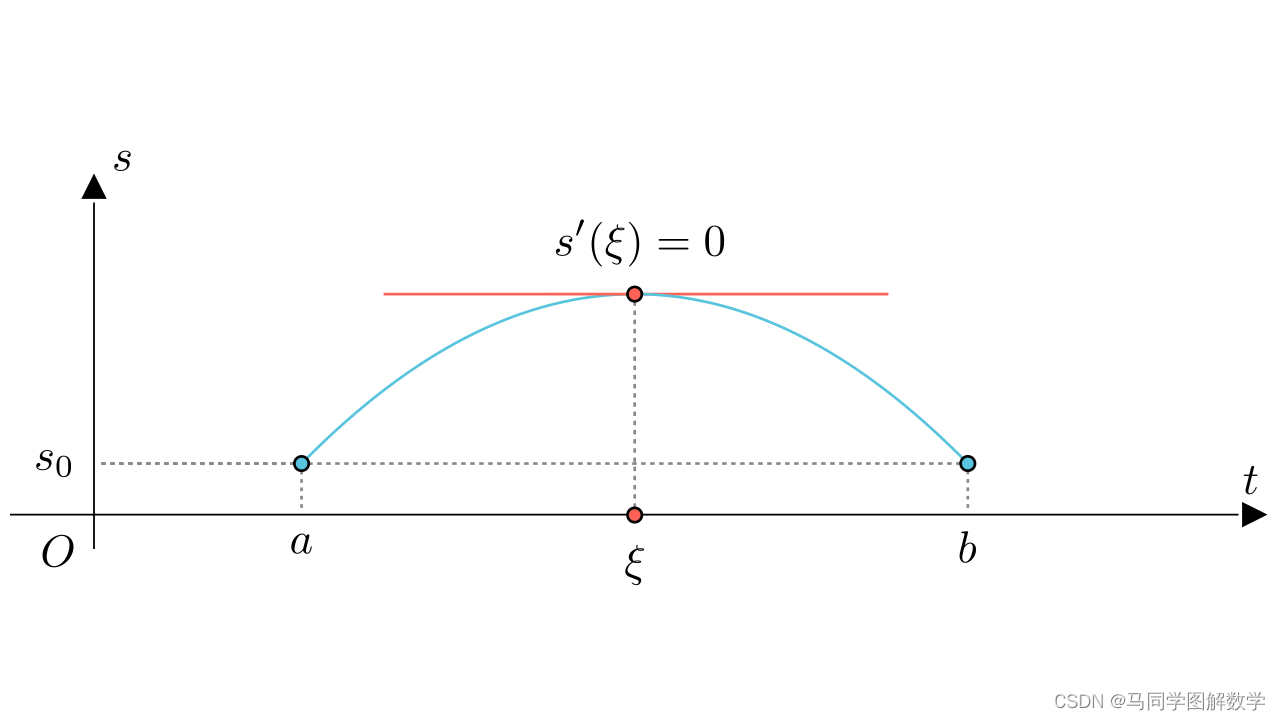
3 细节
3.1 至少一个点导数为零
罗尔中值定理中说的是,导数为零的点至少有一个,隐含意思是,导数为零的点可能有多个。

3.2 开区间可导
不少同学会疑惑,能不能将罗尔中值定理的条件进行如下修改?
答案是不可以,因为这样的修改并不等价,比如:
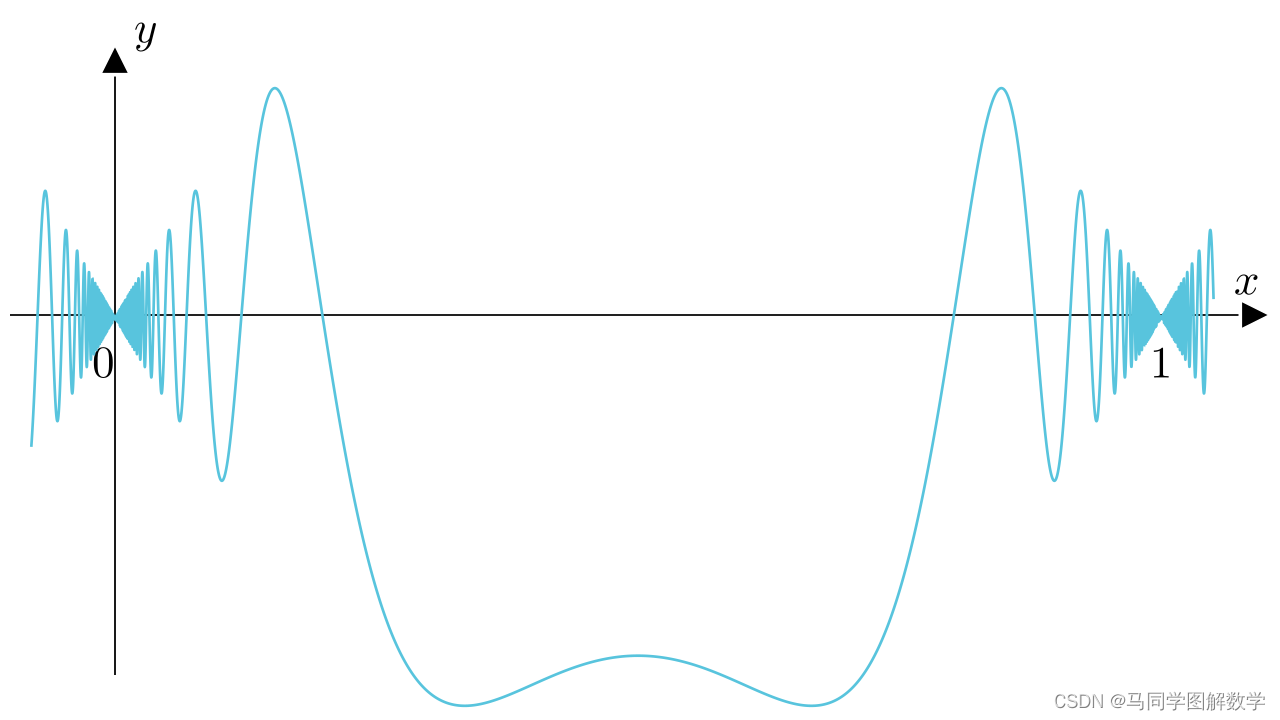
上述函数
就刚好满足“在闭区间
上连续,在开区间
上可导”,其在端点
和
处不可导,它也是可以运用罗尔中值定理的,即
使得
(甚至还有无穷多个):
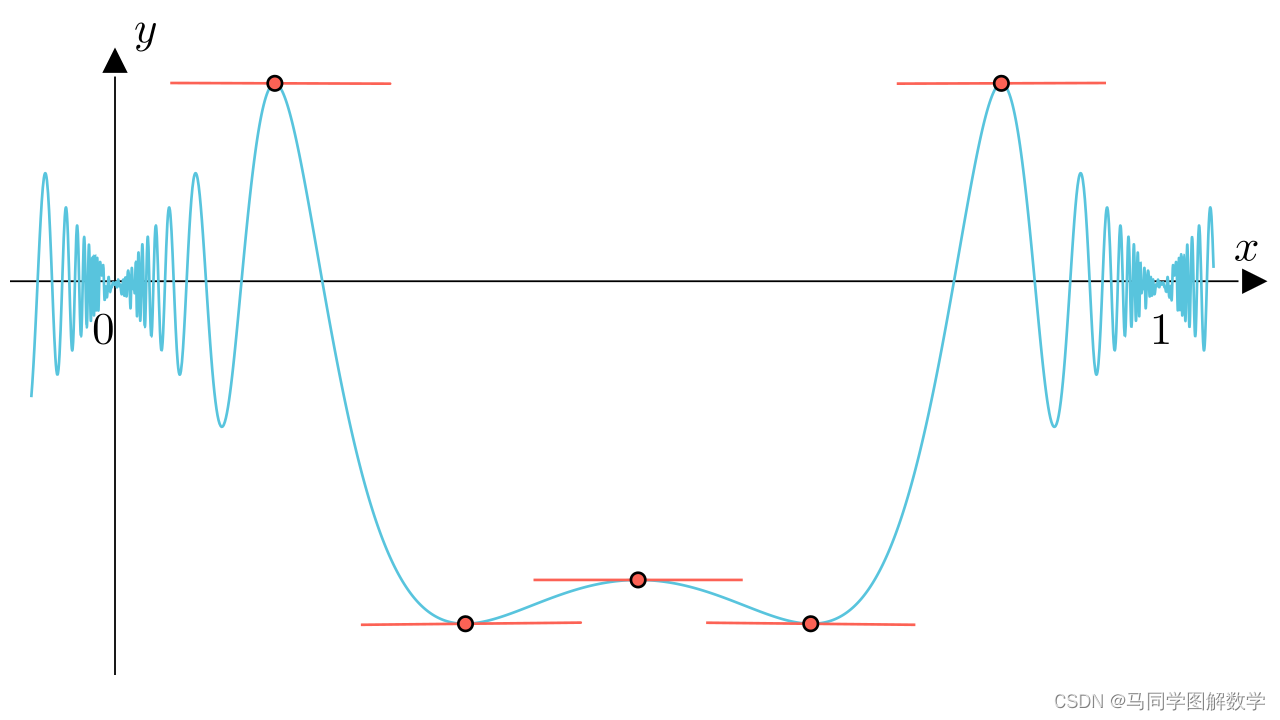
-
-
相关阅读:
Mysql知识点
C++征途 --- List链表容器
千亿播放量!年轻人又迷上了这些解压方式!!!
嵌软工程师要掌握的硬件知识2:一文看懂什么是开漏和推挽电路(open-drain / push-pull)
Springboot考研教材查询系统wi7pz计算机毕业设计-课程设计-期末作业-毕设程序代做
LeetCode 768. 最多能完成排序的块 II
从0开始学习JavaScript--JavaScript类型化数组进阶
day04 51单片机-矩阵按键
创建vue项目教程
ESP8266-Arduino编程实例-OLED显示DS18B20传感器数据
- 原文地址:https://blog.csdn.net/ccnt_2012/article/details/127384372