-
单源赋权最短路径
单源赋权最短路径指给定一个赋权图
和一个输入顶点
,从
出发到图中其他顶点的最短路径就称为单源赋权最短路径。
Djkstra算法:
解决单源赋权最短路径问题的一般方法叫作Djkstra算法(迪杰斯特拉算法)。迪杰斯特拉算法是一种贪婪算法,它是分阶段进行的,在每个阶段都认为选择是最好的。迪杰斯特拉算法只能解决非负权值的最短路径问题。
在该方法中,图中的每个顶点保留与无权最短路径中同样的信息。known表示是否该顶点是否已知,d表示该顶点到输入顶点的距离,path表示引起该顶点距离变化的最后一个顶点,在顶点
的邻接表中,除了要保存邻接顶点的编号外,还要额外保存该顶点到其邻接顶点的边的权值dvw。
迪杰斯特拉算法正是基于这些信息来实现的。首先我们选择d最小的未知顶点
,因为这是我们在这个阶段所能做的最好选择,而且事实上,从输入顶点
开始,首先找到其邻接顶点并改变邻接顶点的d,并标记
为已知,接下来从d最小的未知顶点
开始,显然这个未知顶点的最小距离就是d,因为从
开始,不论从任何其他顶点回到
,都需要经过
以外的边,显然这会导致距离大于d,所以每当我们选择到d最小的未知顶点时,它的最短距离就是d,并且我们可以将它标记为已知。接下来,我们考察
的未知邻接顶点。当顶点
的距离d加上其与邻接顶点之间边的权值dvw小于邻接顶点当前的距离d时,就更新邻接顶点的d,并改变邻接顶点的path,重复上述操作直到所有顶点都变为已知,就解决了单源赋权最短路径问题。
以下图为例,选择输入顶点
为
,通过表格来说明Djkstra算法的具体过程,首先将图中顶点(除
外)的距离d都设置为inf(无穷),显然
的距离d为0.
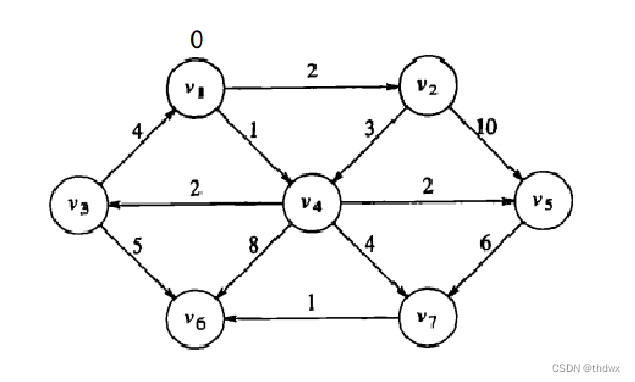
Known d path 0 0 -1 0 inf -1 0 inf -1 0 inf -1 0 inf -1 0 inf -1 0 inf -1 下一步,将
标记为已知(用 * 表示),并处理
的邻接顶点:
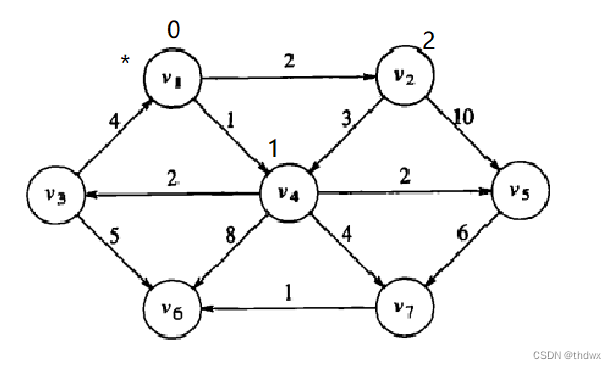
Known d path 1 0 -1 0 2 0 inf -1 0 1 0 inf -1 0 inf -1 0 inf -1 下一步,找到d最小的未知顶点
,做和
相同的处理:
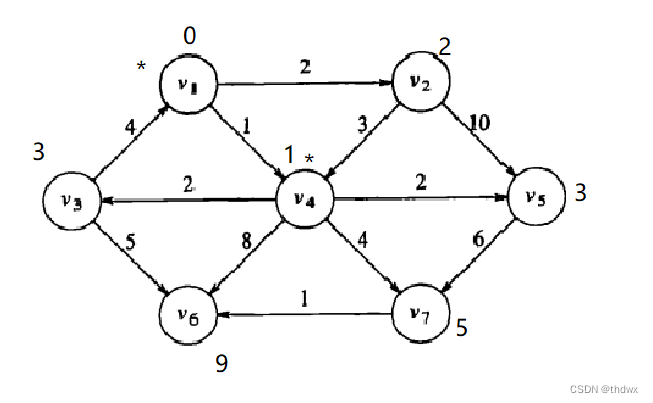
Known d path 1 0 -1 0 2 0 3 1 1 0 3 0 9 0 5 接下来处理
,在处理邻接顶点时,
已知,不做处理,处理
时,因为
当前的d=3,而
的d=2,再加上dvw=10,所以
的d保持不变,path也保持不变。

Known d path 1 0 -1 1 2 0 3 1 1 0 3 0 9 0 5 接下来处理
,同
的处理方法一样,显然
的d和path需要更新:
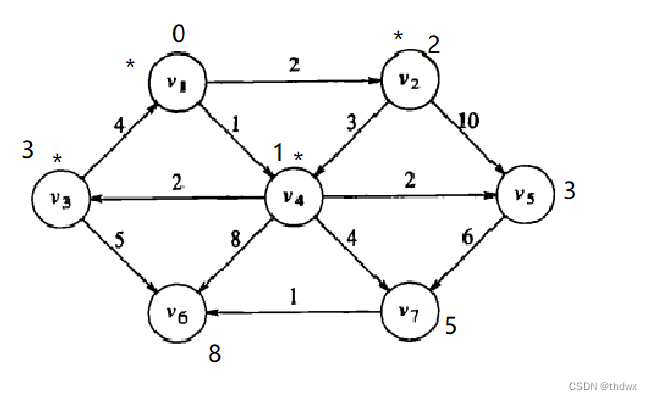
Known d path 1 0 -1 1 2 1 3 1 1 0 3 0 8 0 5 下一步,处理
:
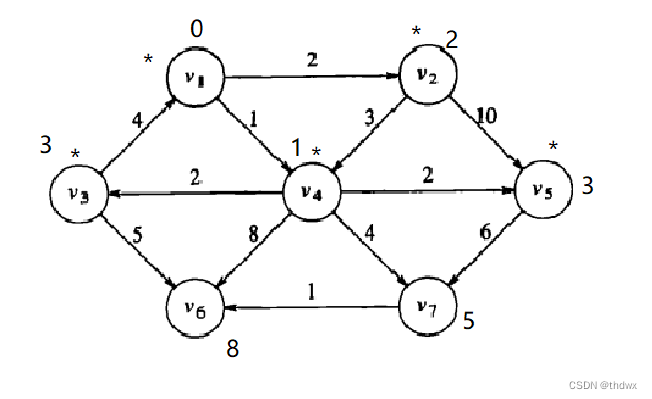
Known d path 1 0 -1 1 2 1 3 1 1 1 3 0 8 0 5 下一步处理
:

Known d path 1 0 -1 1 2 1 3 1 1 1 3 0 8 1 5 最后处理
:
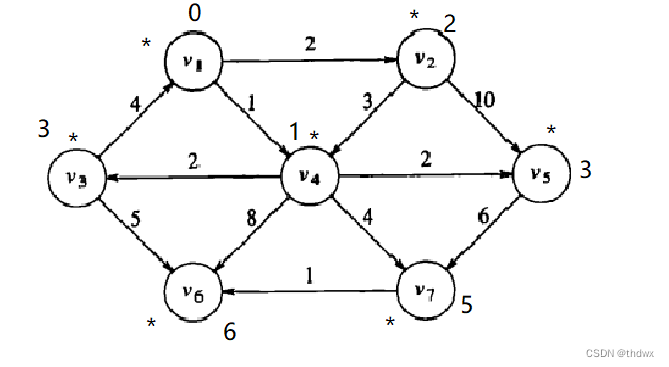
Known d path 1 0 -1 1 2 1 3 1 1 1 3 1 6 1 5 到此就得到了所有顶点的赋权最短路径。
代码实现:
- void Djkstra(g* p) {
- int min, dmin;
- for (;;) {
- dmin = inf;
- int i;
- for (i = 0; i < 7; i++) {//找到d最小的未知顶点
- if (p->v[i]->known == 0 && p->v[i]->d < dmin) {
- dmin = p->v[i]->d;
- min = i;
- }
- }
- if (dmin == inf) {//dmin没有改变说明要么所有顶点都是已知,要么虽然有的顶点未知,但是从输入顶点出发不能到达,这两种情况都应该退出循环
- break;
- }
- p->v[min]->known = 1;
- l* tmp = p->v[min]->next;
- while (tmp != NULL) {//处理min顶点的邻接顶点
- if (p->v[tmp->val]->known == 0) {
- if (p->v[min]->d + tmp->dvw < p->v[tmp->val]->d) {
- p->v[tmp->val]->d = p->v[min]->d + tmp->dvw;
- p->v[tmp->val]->path = min;
- }
- }
- tmp = tmp->next;
- }
- }
- }
显然,Djkstra算法包含两层for循环,所以它的时间复杂度为
。
Djkstra算法能够处理没有负边的赋权最短路径问题,但是它并不能解决有负边的最短路径问题,这是因为Djkstra算法对已知的顶点不会再做处理,但是有负边时,已知的顶点有可能邻接于其之后处理的顶点,而从这个顶点返回已知顶点的路径更短,这个时候Djkstra算法就不能正确的更新d以及path。
带有负值边的赋权最短路径:
一种处理具有负边图的办法是:给所有边都加上一个常数C,使得所有边都变为正值,这种方法看似可行,实际上那些具有较多边的路径的权重会大于那些较少边的路径,即使之前它们之间的关系不是这样。
另一种方法是:将赋权和无权的方法结合起来,但是舍弃掉Known这个信息。这种方法使用一个队列来存放将要处理的顶点,首先将
入队,当队列不为空时,队头顶点出队,然后对该顶点的邻接顶点的信息进行更新,并将更新过且不在队列中的顶点入队,重复操作直到队列为空。这个算法基于这样一个事实,如果存在负边,那么所有顶点当前的d都不一定是最小的,那么它们可能仍然需要被更新,所以当处理完当前顶点后,如果该顶点的邻接顶点信息被改变,那么该邻接顶点的邻接顶点信息也要被改变。
但是如果负值边指向的顶点能够到达图中的任何一个其他顶点(如图),那么这种方法就可能陷入死循环,这个时候就必须设置终止条件,这个条件可以是在任意顶点已经出队
次后。在图中,每个顶点的最小d实际上应该是负无穷(如果一直循环下去)。但如果将-10改为-2或是-1,那么这条边又会变得没有意义,因为经过这条边到达
并不会比
本来的d更小。实际上可以总结为,如果能通过负边减小d的顶点,就可以通过不断地经过负边来使它的d越来越小,而不能通过负边改变d的顶点,它们的信息也就与没有负边时相同。并且在现实生活中,负的权值是很少见的,我们一般处理的权值,比如价格、距离、时间等因素,都是非负的。
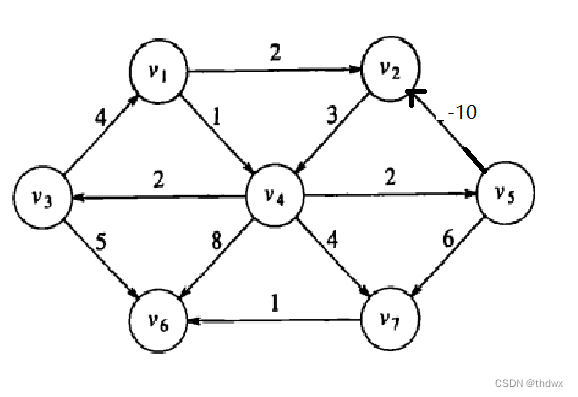
使用队列的赋权最短路径算法:
- void WeightedNegative(g* p) {
- q* pq = CreatQueue();//建立队列
- enqueue(pq, 0);//将输入顶点s入队
- p->v[0]->known = 1;//将该顶点标记为已在队列中
- while (!isempty(pq)) {//当队列不为空时
- int n = dequeue(pq);//出队
- p->v[n]->known = 0;//将出队顶点标记为不在队中
- if (p->v[n]->dequeuenum == 8)//循环结束条件
- break;
- p->v[n]->dequeuenum++;//出队后,出队次数+1
- l* tmp = p->v[n]->next;
- while (tmp != NULL) {//对出队顶点的邻接顶点更新,如果邻接顶点更新了就入队
- if (p->v[n]->d + tmp->dvw < p->v[tmp->val]->d) {
- p->v[tmp->val]->d = p->v[n]->d + tmp->dvw;
- p->v[tmp->val]->path = n;
- if (p->v[tmp->val]->known == 0) {
- enqueue(pq, tmp->val);
- p->v[tmp->val]->known = 1;
- }
- }
- tmp = tmp->next;
- }
- }
- }
运行结果:
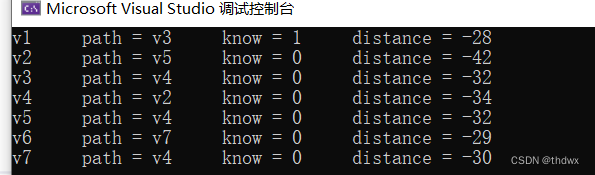
将循环结束条件改为
:
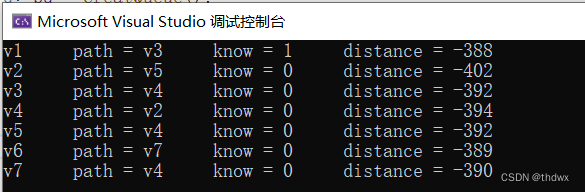
将循环结束条件改为
:
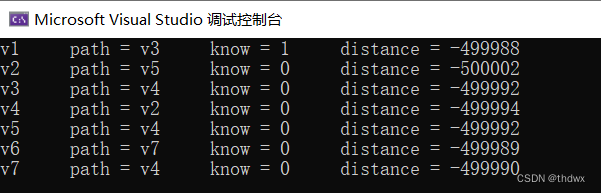
将图中的-10改为-2,运行结果为:
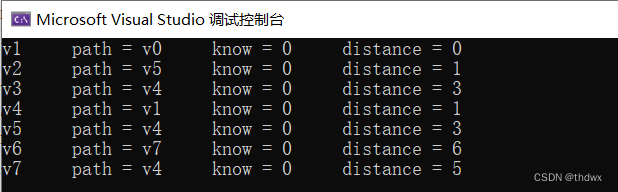
可以看到此时的运行结果和没有负边的结果是相同的。
图的建立和测试代码:
- #define inf 99999999
- //图
- typedef struct list {//邻接表
- int val;
- int dvw;
- struct list* next;
- }l;
- typedef struct table {//图中顶点的信息
- int known;
- int d;
- int path;
- int dequeuenum;
- l* next;//指向邻接表的指针
- }t;
- typedef struct graph {//指向定点信息的指针
- t* v[7];
- }g;
- g* CreatGraph() {
- g* pg = (g*)malloc(sizeof(g));
- for (int i = 0; i < 7; i++) {
- t* p = (t*)malloc(sizeof(t));
- p->next = NULL;
- p->d = inf;
- p->known = 0;
- p->path = -1;
- p->dequeuenum = 0;
- pg->v[i] = p;
- }
- l* p = (l*)malloc(sizeof(l));
- p->val = 1;
- p->dvw = 2;
- p->next = pg->v[0]->next;
- pg->v[0]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 3;
- p->dvw = 1;
- p->next = pg->v[0]->next;
- pg->v[0]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 3;
- p->dvw = 3;
- p->next = pg->v[1]->next;
- pg->v[1]->next = p;
- /*p = (l*)malloc(sizeof(l));
- p->val = 4;
- p->dvw = 10;
- p->next = pg->v[1]->next;
- pg->v[1]->next = p;*/
- p = (l*)malloc(sizeof(l));
- p->val = 0;
- p->dvw = 4;
- p->next = pg->v[2]->next;
- pg->v[2]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 5;
- p->dvw = 5;
- p->next = pg->v[2]->next;
- pg->v[2]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 2;
- p->dvw = 2;
- p->next = pg->v[3]->next;
- pg->v[3]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 4;
- p->dvw = 2;
- p->next = pg->v[3]->next;
- pg->v[3]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 5;
- p->dvw = 8;
- p->next = pg->v[3]->next;
- pg->v[3]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 6;
- p->dvw = 4;
- p->next = pg->v[3]->next;
- pg->v[3]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 6;
- p->dvw = 6;
- p->next = pg->v[4]->next;
- pg->v[4]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 1;
- p->dvw = -10;
- p->next = pg->v[4]->next;
- pg->v[4]->next = p;
- p = (l*)malloc(sizeof(l));
- p->val = 5;
- p->dvw = 1;
- p->next = pg->v[6]->next;
- pg->v[6]->next = p;
- return pg;
- }
- //队列
- typedef struct queue {
- int arr[50];
- int front;
- int rear;
- int num;
- }q;
- int dequeue(q* p) {
- p->num--;
- return p->arr[p->front++ % 50];
- }
- void enqueue(q* p, int x) {
- p->num++;
- p->arr[(++p->rear) % 50] = x;
- }
- q* CreatQueue() {
- q* p = (q*)malloc(sizeof(q));
- p->front = 0;
- p->rear = -1;
- p->num = 0;
- return p;
- }
- int isempty(q* p) {
- return p->num == 0;
- }
- //打印函数
- void print(g* p) {
- for (int i = 0; i < 7; i++) {
- printf("v%d path = v%d know = %d distance = %d\n", i + 1, p->v[i]->path + 1, p->v[i]->known, p->v[i]->d);
- }
- }
- //测试函数
- int main() {
- g* pg = CreatGraph();
- pg->v[0]->d = 0;
- WeightedNegative(pg);
- print(pg);
- return 0;
- }
-
相关阅读:
SpringCloud - Spring Cloud Netflix 之 Hystrix ;turbine(十)
【JavaEE】多线程(四)
Lfu缓存在Rust中的实现及源码解析
猿创征文|【C++之new和delete运算符】创建数组
【毕业设计】基于javaEE+SSH+mysql的码头船只出行及配套货柜码放管理系统设计与实现(毕业论文+程序源码)——码头船只出行及配套货柜码放管理系统
电脑网速慢怎么解决?推荐这3个方法
【0205】哪些信号可kill掉postmaster?内核如何实现?
中国地表水体、大坝、水库和湖泊数据集
【图文详解】深入理解 Hbase 架构 Deep Into HBase Architecture
AJAX为什么叫AJAX
- 原文地址:https://blog.csdn.net/thdwx/article/details/127442385
