【概率论与数理统计】

一、概率论的基本概念

1.1 样本空间，样本点，随机试验

样本空间：所有可能结果的集合
样本点：样本空间的一个结果
随机试验：结果未知（所有结果已知），可重复，多种结果
例子：扔骰子的点数
样本空间：{1,2，3,4，5,6}
样本点：其中任何一个点数

1.2事件的关系及其运算

事件关系

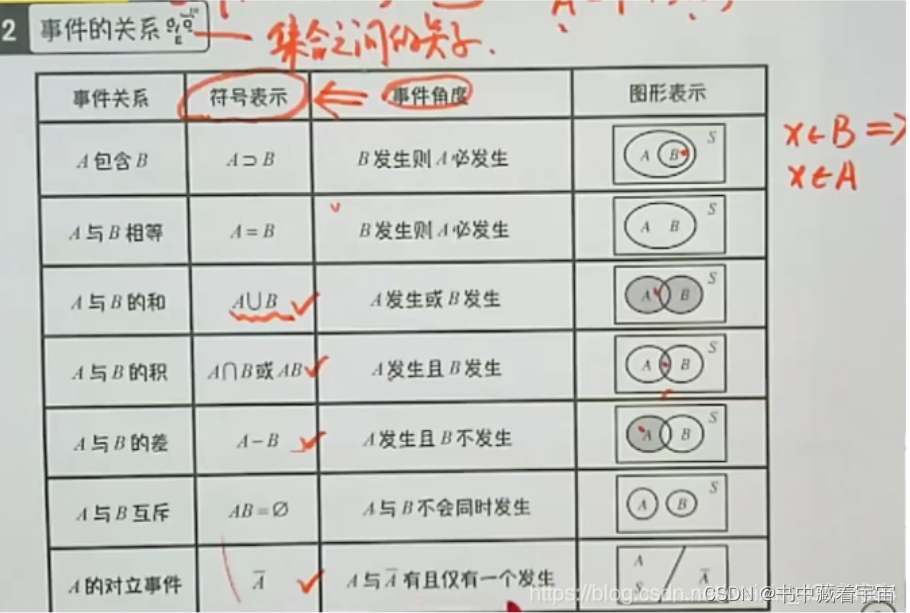
事件运算
-------------------------------------------------------------------------
P（A）=1-P（A非）
P（A+B）=P（A）+P（B）-P（AB）
P（A-B）=P（A）-P（AB）
-------------------------------------------------------------------------

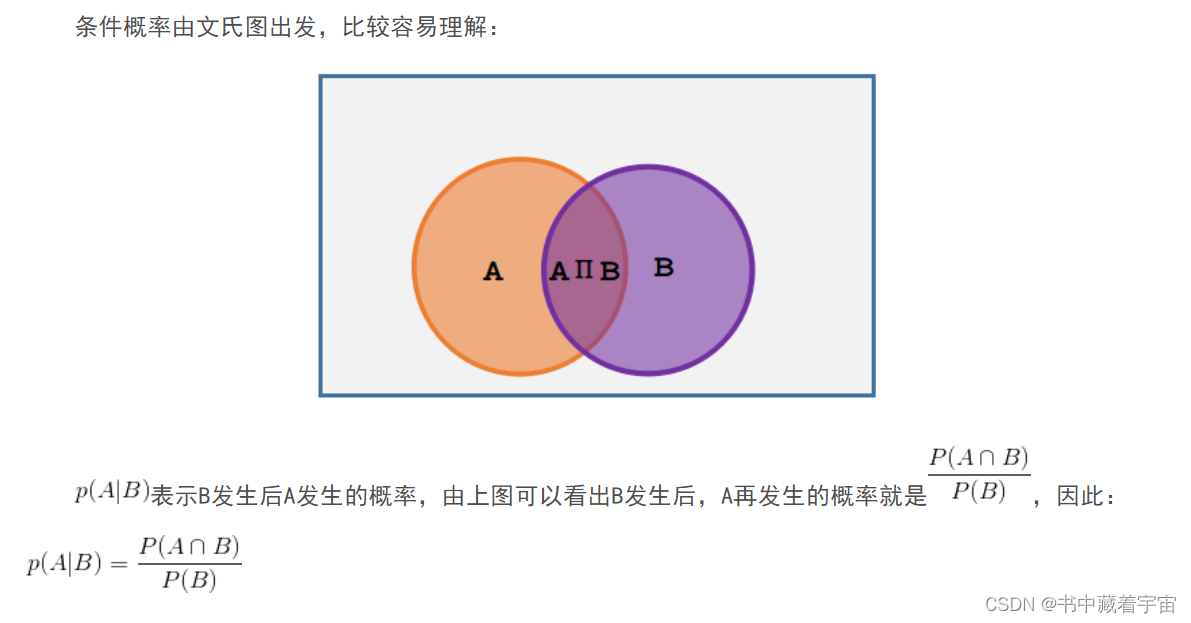
1.3 条件概率

1.4全概率与贝叶斯

全概率：也就是我们常说的先验概率。比如我们在回家过程中，有三条路可以去公司，但是每条路都假设有一个迟到概率，现在问某人迟到的概率是多少？


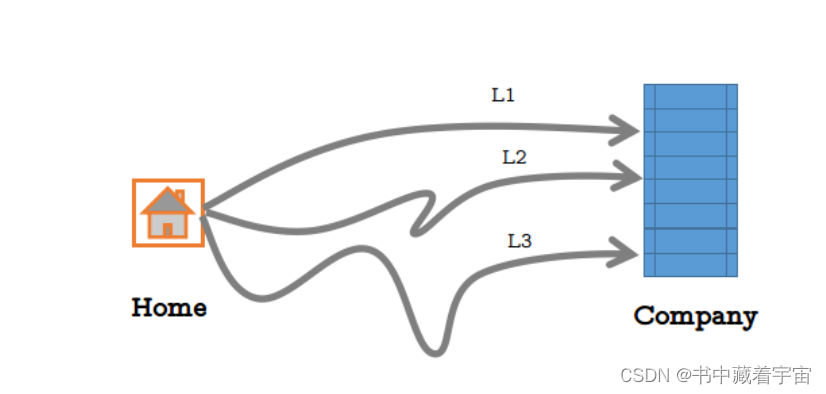
贝叶斯：贝叶斯就是我们所说的后验概率，就是我们已经知道我们已经迟到的情况下，问是选了某条路迟到的概率。

二、随机变量及其分布

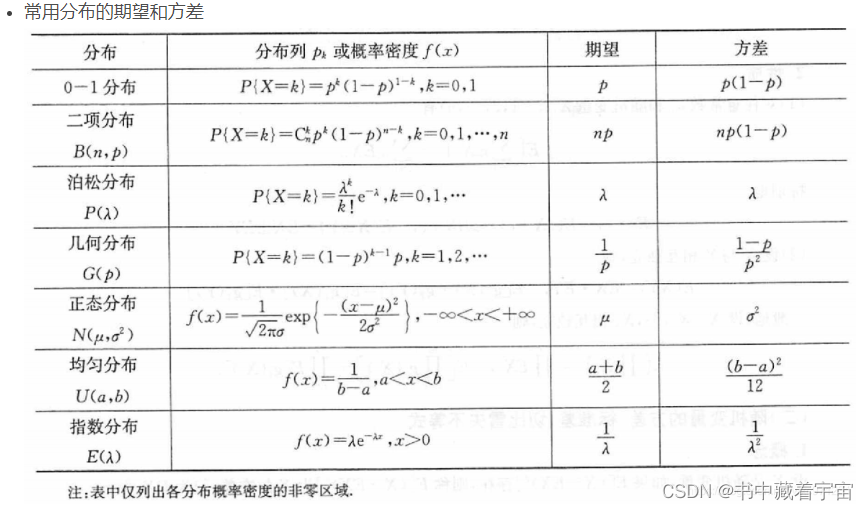
2.1 离散分布

定义：随机变量为离散型，即所说的可能的结果为离散的
（1）0-1分布

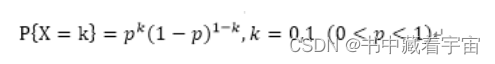
（2）二项分布
当重复做某种实验时，某一种结果出现次数的概率

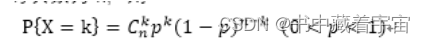
1.3possion分布

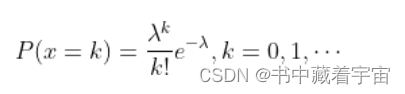
2.2 连续分布

（1）高斯分布

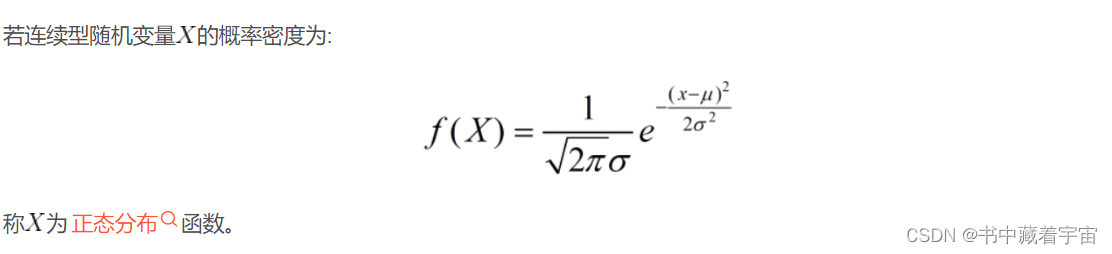
（2）均匀分布

（3）指数分布

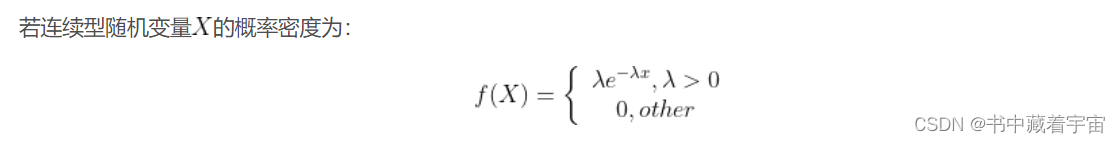
三、多维随机变量及其分布

定义：
规律：

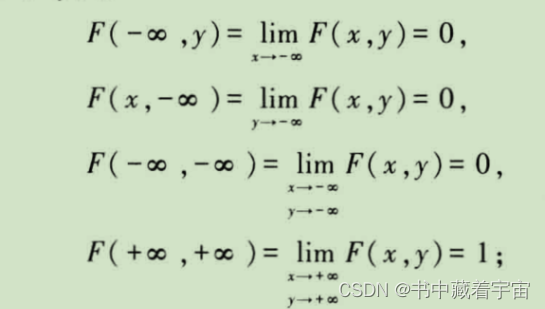
边缘分布

二维正态分布

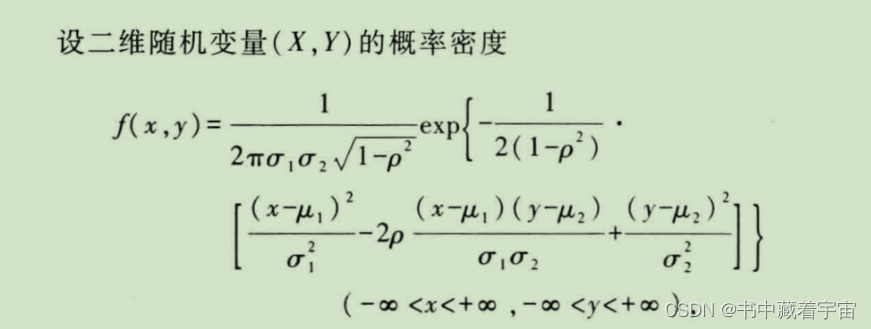
其中：

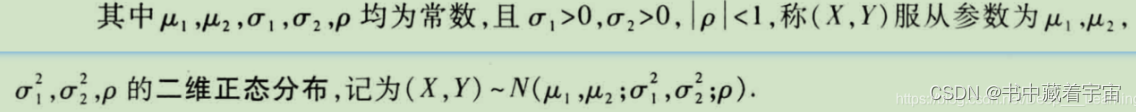
示意图

四、 随机变量及其数字特征

4.1 期望

（1）离散型

（2）数字型

推广

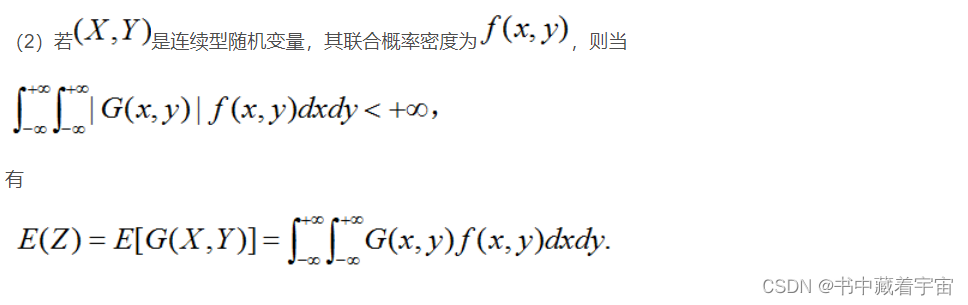
4.2性质

4.3 方差

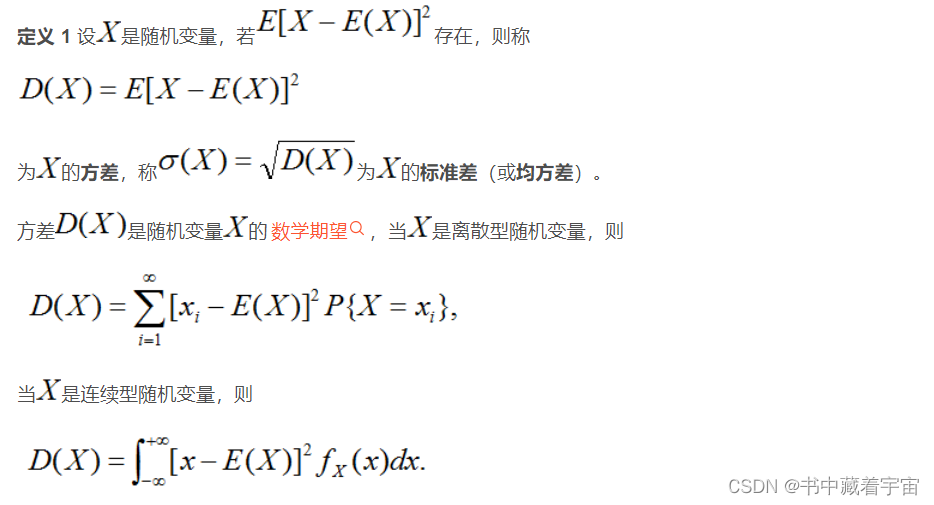
性质

------------------------------------------------------------------

------------------------------------------------------------------

-------------------------------------------------------------------
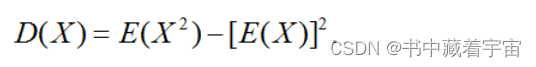
备注：协方差性质


--------------------------------------------------------------------
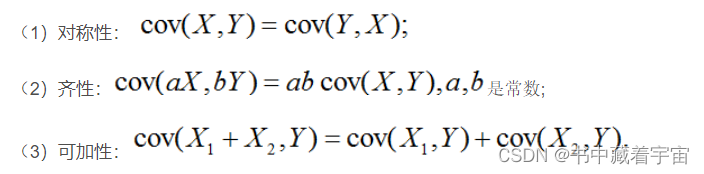
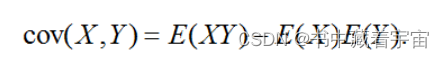
相关函数

五、大数定律及其中心极限定理

参考资料
链接: linkhttps://blog.csdn.net/qq_41437512/article/details/106408437?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166627004616782425163441%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=166627004616782425163441&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-106408437-null-null.142^v59pc_rank_34_1,201^v3add_ask&utm_term=%E5%A4%A7%E6%95%B0%E5%AE%9A%E5%BE%8B%E4%B8%8E%E4%B8%AD%E5%BF%83%E6%9E%81%E9%99%90&spm=1018.2226.3001.4187

六、样本及其抽样分布

统计量



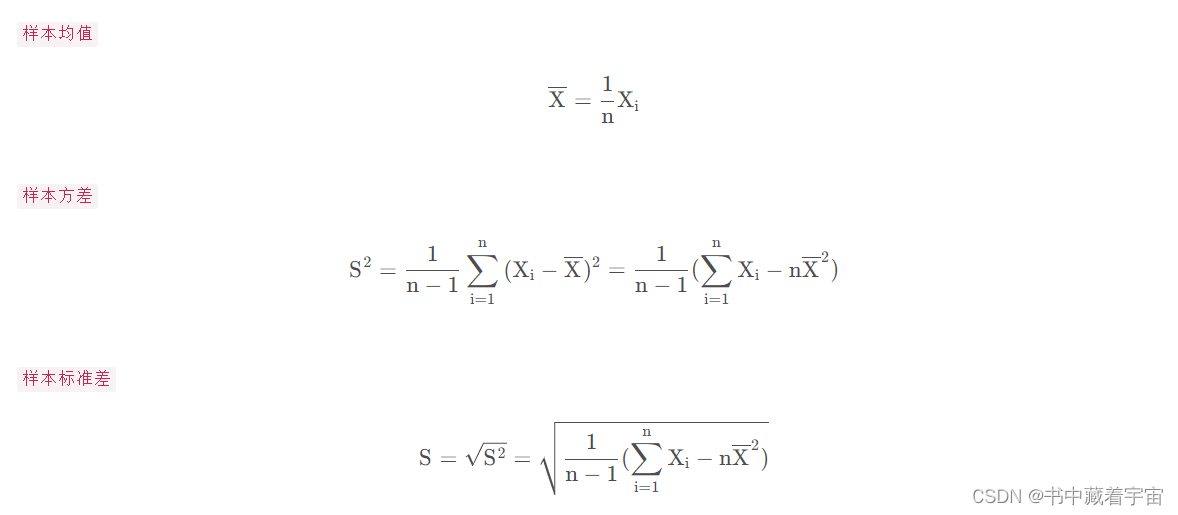
三大分布

-------------------------------------------------------------------------

------------------------------------------------------------------------------

备注：总体正态分布的样本情况
样本均值与样本方差


------------------------------------------------------------
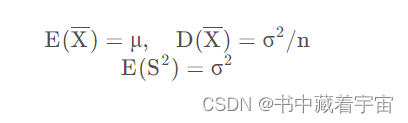
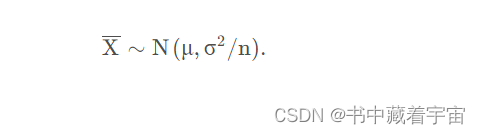
样本均值与样本方差是独立的

----------------------------------------------------------------------
t分布

-------------------------------------------------------------------------------

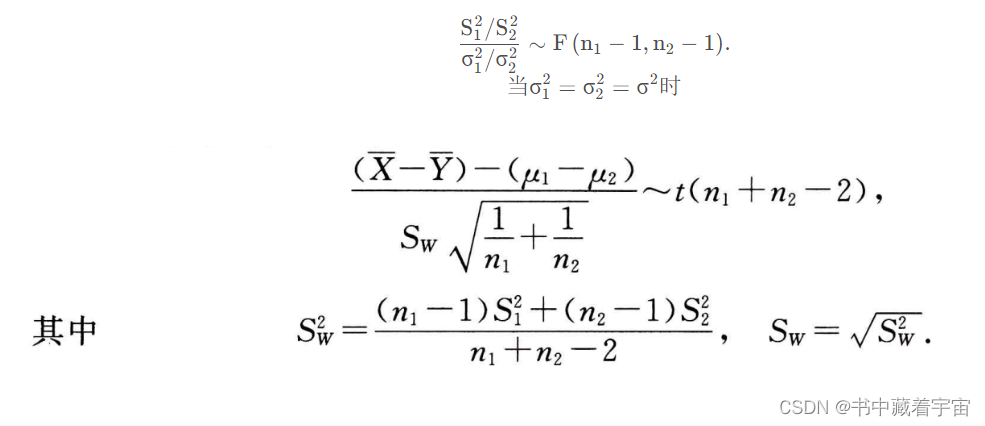
七、参数估计

7.1点估计

核心原理：令总体的k阶原点矩等于它样本的k阶原点矩

7.2 区间估计

区间估计是依据抽取的样本，根据一定的正确度与精确度的要求，构造出适当的区间，作为总体分布的未知参数或参数的函数的真值所在范围的估计。

例如人们常说的有百分之多少的把握保证某值在某个范围内，即是区间估计的最简单的应用。

求置信区间常用的三种方法:

利用已知的抽样分布。
利用区间估计与假设检验的联系。
利用大样本理论。
区间估计可以告知置信区间范围，但不能直接告知人们“未知参数是多少”。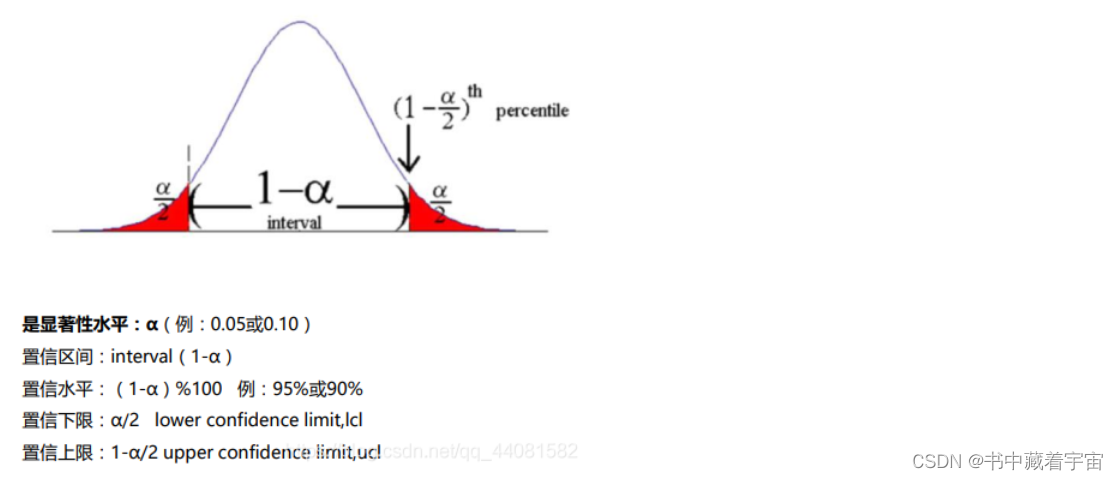

八、假设检验

九、随机过程