games101——作业5

---

总览

在这部分的课程中，我们将专注于使用光线追踪来渲染图像。在光线追踪中
最重要的操作之一就是找到光线与物体的交点。一旦找到光线与物体的交点，就可以执行着色并返回像素颜色。在这次作业中，我们需要实现两个部分：光线的生成和光线与三角的相交。本次代码框架的工作流程为：

1. 从 main 函数开始。我们定义场景的参数，添加物体（球体或三角形）到场景中，并设置其材质，然后将光源添加到场景中。
2. 调用 Render(scene) 函数。在遍历所有像素的循环里，生成对应的光线并将返回的颜色保存在帧缓冲区（framebuffer）中。在渲染过程结束后，帧缓冲区中的信息将被保存为图像。
3. 在生成像素对应的光线后，我们调用 CastRay 函数，该函数调用 trace 来查询光线与场景中最近的对象的交点。
4. 然后，我们在此交点执行着色。我们设置了三种不同的着色情况，并且已经为你提供了代码。
   你需要修改的函数是：
   • Renderer.cpp 中的 Render()：这里你需要为每个像素生成一条对应的光线，然后调用函数 castRay() 来得到颜色，最后将颜色存储在帧缓冲区的相应像素中。
   • Triangle.hpp 中的 rayTriangleIntersect(): v0, v1, v2 是三角形的三个顶点，orig 是光线的起点，dir 是光线单位化的方向向量。tnear, u, v 是你需要使用我们课上推导的 Moller-Trumbore 算法来更新的参数。

---

开始编写

在本次作业中，你将使用一个新的代码框架。和之前作业相似的是，你可以
选择在自己电脑的系统或者虚拟机上完成作业。请下载项目的框架代码，并使用以下命令像以前一样构建项目：

$ mkdir build
$ cd build
$ cmake ..
$ make
1
2
3
4

之后，你就可以使用./Raytracing 来运行代码。现在我们对代码框架中的一
些类做一下概括性的介绍：
• global.hpp：包含了整个框架中会使用的基本函数和变量。
• Vector.hpp: 由于我们不再使用 Eigen 库，因此我们在此处提供了常见的向量操作，例如：dotProduct，crossProduct，normalize。
• Object.hpp: 渲染物体的父类。Triangle 和 Sphere 类都是从该类继承的。
• Scene.hpp: 定义要渲染的场景。包括设置参数，物体以及灯光。
• Renderer.hpp: 渲染器类，它实现了所有光线追踪的操作。

---

代码框架详解

main.cpp

从 main.cpp 入手，首先将场景的屏幕的尺寸为 $1280\times 960$

Scene scene(1280, 960);
1

然后在场景中的加入了两个球体 sph1 与 sph2，创建时指定其球心坐标以及半径，sph1 的反射类型为漫反射，sph2 的反射类型为反射+折射，ior 为其材质折射率

auto sph1 = std::make_unique<Sphere>(Vector3f(-1, 0, -12), 2);
sph1->materialType = DIFFUSE_AND_GLOSSY;
sph1->diffuseColor = Vector3f(0.6, 0.7, 0.8);

auto sph2 = std::make_unique<Sphere>(Vector3f(0.5, -0.5, -8), 1.5);
sph2->ior = 1.5;
sph2->materialType = REFLECTION_AND_REFRACTION;

scene.Add(std::move(sph1));
scene.Add(std::move(sph2));
1
2
3
4
5
6
7
8
9
10

之后又在场景中加入了两个三角形，或者说是一个由两个三角形组成的矩形，设定其顶点坐标，st坐标，以及反射类型为漫反射

Vector3f verts[4] = {{-5,-3,-6}, {5,-3,-6}, {5,-3,-16}, {-5,-3,-16}};
uint32_t vertIndex[6] = {0, 1, 3, 1, 2, 3};
Vector2f st[4] = {{0, 0}, {1, 0}, {1, 1}, {0, 1}};
auto mesh = std::make_unique<MeshTriangle>(verts, vertIndex, 2, st);
mesh->materialType = DIFFUSE_AND_GLOSSY;

scene.Add(std::move(mesh));
1
2
3
4
5
6
7

然后再在场景中加入两个点光源，初始化其点光源的坐标与光线强度

scene.Add(std::make_unique<Light>(Vector3f(-20, 70, 20), 0.5));
scene.Add(std::make_unique<Light>(Vector3f(30, 50, -12), 0.5));
1
2

最后渲染场景

Renderer r;
r.Render(scene);
1
2

Render

在 Render 方法中，首先定义了尺度scale与宽高比imageAspectRatio，以及相机位置在 $(0,0,0)$。

std::vector<Vector3f> framebuffer(scene.width * scene.height);

float scale = std::tan(deg2rad(scene.fov * 0.5f));
float imageAspectRatio = scene.width / (float)scene.height;

// Use this variable as the eye position to start your rays.
Vector3f eye_pos(0);
int m = 0;
1
2
3
4
5
6
7
8

然后对于每一个像素，从相机向像素射出一条射线，这里屏幕要从光栅空间转换到世界空间中，具体说明放在作业代码部分。

对于射出的光线获得的颜色，使用 castRay 获取，获取到的颜色信息保存到 framebuffer 中，最后写入 binary.ppm 文件中

// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
     static unsigned char color[3];
     color[0] = (char)(255 * clamp(0, 1, framebuffer[i].x));
     color[1] = (char)(255 * clamp(0, 1, framebuffer[i].y));
     color[2] = (char)(255 * clamp(0, 1, framebuffer[i].z));
     fwrite(color, 1, 3, fp);
}
fclose(fp); 
1
2
3
4
5
6
7
8
9
10
11

下面具体看 castRay 里的代码

castRay

一开始对 depth 进行比较，这里应该是对光线折射次数的定义（因为Whitted风格的光线追踪考虑光线是不断反射的），在这里场景中的光线折射次数限定为 5 次。然后给颜色初始化为背景颜色

if (depth > scene.maxDepth) {
   return Vector3f(0.0,0.0,0.0);
}
Vector3f hitColor = scene.backgroundColor;
1
2
3
4

然后使用 trace 判断光线是否与场景中的物体有交点，有交点执行之后的代码，没有交点直接返回背景颜色

if (auto payload = trace(orig, dir, scene.get_objects()); payload)
1

在 trace 获得的 payload->tNear 按照光线方程，可以计算出对应的交点坐标 hitPoint。

Vector3f hitPoint = orig + dir * payload->tNear;
1

然后使用 getSurfaceProperties 计算交点所在平面的法向量，以及交点的st坐标(只有三角形有)。

Vector3f N; // normal
Vector2f st; // st coordinates
payload->hit_obj->getSurfaceProperties(hitPoint, dir, payload->index, payload->uv, N, st);
1
2
3

对于球体求法向量，就是球中心连向交点就是法向量方向

    void getSurfaceProperties(const Vector3f& P, const Vector3f&, const uint32_t&, const Vector2f&,
                              Vector3f& N, Vector2f&) const override
    {
        N = normalize(P - center);
    }
1
2
3
4
5

对于三角形求法向量，就是两个边法向量的叉积

    void getSurfaceProperties(const Vector3f&, const Vector3f&, const uint32_t& index, const Vector2f& uv, Vector3f& N,
                              Vector2f& st) const override
    {
        const Vector3f& v0 = vertices[vertexIndex[index * 3]];
        const Vector3f& v1 = vertices[vertexIndex[index * 3 + 1]];
        const Vector3f& v2 = vertices[vertexIndex[index * 3 + 2]];
        Vector3f e0 = normalize(v1 - v0);
        Vector3f e1 = normalize(v2 - v1);
        N = normalize(crossProduct(e0, e1));
        const Vector2f& st0 = stCoordinates[vertexIndex[index * 3]];
        const Vector2f& st1 = stCoordinates[vertexIndex[index * 3 + 1]];
        const Vector2f& st2 = stCoordinates[vertexIndex[index * 3 + 2]];
        st = st0 * (1 - uv.x - uv.y) + st1 * uv.x + st2 * uv.y;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

然后就是根据触碰到的物体的材质，执行不同的算法获得对应颜色

switch (payload->hit_obj->materialType)
1

REFLECTION_AND_REFRACTION

字面意思，既有反射也有折射，首先使用reflect函数计算反射方向，reflect 函数如下

// Compute reflection direction
Vector3f reflect(const Vector3f &I, const Vector3f &N)
{
    return I - 2 * dotProduct(I, N) * N;
}
1
2
3
4
5

然后使用refract函数计算折射方向，refract 函数如下

Vector3f refract(const Vector3f &I, const Vector3f &N, const float &ior)
{
    float cosi = clamp(-1, 1, dotProduct(I, N));
    float etai = 1, etat = ior;
    Vector3f n = N;
    if (cosi < 0) { cosi = -cosi; } else { std::swap(etai, etat); n= -N; }
    float eta = etai / etat;
    float k = 1 - eta * eta * (1 - cosi * cosi);
    return k < 0 ? 0 : eta * I + (eta * cosi - sqrtf(k)) * n;
}
1
2
3
4
5
6
7
8
9
10

折射方向推导如下


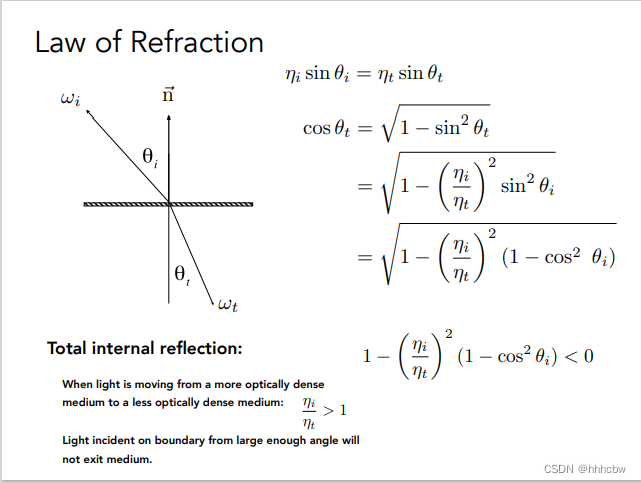
然后计算反射光线与折射光线的起始点，这里为什么要 $\pm N\ast epsilon$，是因为之后可能会继续判断射线是否与物体有接触，所以要加上或减取一个很小的值，防止有接触到当前点。

Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
                                             hitPoint - N * scene.epsilon :
                                             hitPoint + N * scene.epsilon;
Vector3f refractionRayOrig = (dotProduct(refractionDirection, N) < 0) ?
                                             hitPoint - N * scene.epsilon :
                                             hitPoint + N * scene.epsilon;
1
2
3
4
5
6

然后因为在 Whitted风格的光线追踪模型中 REFLECTION_AND_REFRACTION 的光完全由反射和折射光决定，所以之后再用 castRay 计算出反射颜色reflectionColor与折射颜色refractionColor。

Vector3f reflectionColor = castRay(reflectionRayOrig, reflectionDirection, scene, depth + 1);
Vector3f refractionColor = castRay(refractionRayOrig, refractionDirection, scene, depth + 1);
1
2

那么涉及到反射与折射，使用菲涅尔项计算出对应的反射比例kr，然后加权出对应的颜色 hitColor

float kr = fresnel(dir, N, payload->hit_obj->ior);
hitColor = reflectionColor * kr + refractionColor * (1 - kr);
break;
1
2
3

fresnel 的对应公式与代码如下

float fresnel(const Vector3f &I, const Vector3f &N, const float &ior)
{
    float cosi = clamp(-1, 1, dotProduct(I, N));
    float etai = 1, etat = ior;
    if (cosi > 0) {  std::swap(etai, etat); }
    // Compute sini using Snell's law
    float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi));
    // Total internal reflection
    if (sint >= 1) {
        return 1;
    }
    else {
        float cost = sqrtf(std::max(0.f, 1 - sint * sint));
        cosi = fabsf(cosi);
        float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost));
        float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost));
        return (Rs * Rs + Rp * Rp) / 2;
    }
    // As a consequence of the conservation of energy, transmittance is given by:
    // kt = 1 - kr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

REFLECTION

这个与上面 REFLECTION_AND_REFRACTION类似，就是没有折射项。

 case REFLECTION:
{
        float kr = fresnel(dir, N, payload->hit_obj->ior);
         Vector3f reflectionDirection = reflect(dir, N);
         Vector3f reflectionRayOrig = (dotProduct(reflectionDirection, N) < 0) ?
                                             hitPoint + N * scene.epsilon :
                                             hitPoint - N * scene.epsilon;
         hitColor = castRay(reflectionRayOrig, reflectionDirection, scene, depth + 1) * kr;
         break;
}
1
2
3
4
5
6
7
8
9
10

default(DIFFUSE_AND_GLOSSY)

默认项就是漫反射类型的材质，其使用 Phong 模型计算对应的漫反射项与镜面反射项。其公式如下，这里不使用 $L_a$ 项：

首先判断当前点与光线的连线是否与物体接触(即是否被遮挡住)，如果被遮挡住，其 漫反射项 lightAmt 就是 0

Vector3f lightDir = light->position - hitPoint;
// square of the distance between hitPoint and the light
float lightDistance2 = dotProduct(lightDir, lightDir);
lightDir = normalize(lightDir);
float LdotN = std::max(0.f, dotProduct(lightDir, N));
// is the point in shadow, and is the nearest occluding object closer to the object than the light itself?
auto shadow_res = trace(shadowPointOrig, lightDir, scene.get_objects());
bool inShadow = shadow_res && (shadow_res->tNear * shadow_res->tNear < lightDistance2);

lightAmt += inShadow ? 0 : light->intensity * LdotN;
1
2
3
4
5
6
7
8
9
10

然后计算出镜面反射项

Vector3f reflectionDirection = reflect(-lightDir, N);

specularColor += powf(std::max(0.f, -dotProduct(reflectionDirection, dir)),
payload->hit_obj->specularExponent) * light->intensity;
1
2
3
4

当前点的 hitColor 就是漫反射项*Kd+镜面反射项*Ks，这里使用 evalDiffuseColor(st) 渲染出地板的效果，具体什么原理还未搞懂，欢迎大佬指教

hitColor = lightAmt * payload->hit_obj->evalDiffuseColor(st) * payload->hit_obj->Kd + specularColor * payload->hit_obj->Ks;
break;
1
2

trace

trace 就是判断当前射线是否与空间中的物体有交点，如果有交点，返回最近的交点。

std::optional<hit_payload> trace(
        const Vector3f &orig, const Vector3f &dir,
        const std::vector<std::unique_ptr<Object> > &objects)
{
    float tNear = kInfinity;
    std::optional<hit_payload> payload;
    for (const auto & object : objects)
    {
        float tNearK = kInfinity;
        uint32_t indexK;
        Vector2f uvK;
        if (object->intersect(orig, dir, tNearK, indexK, uvK) && tNearK < tNear)
        {
            payload.emplace();
            payload->hit_obj = object.get();
            payload->tNear = tNearK;
            payload->index = indexK;
            payload->uv = uvK;
            tNear = tNearK;
        }
    }

    return payload;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

当然每个物体判断方式各不相同，这里放在作业代码部分进一步说明

---

作业代码

屏幕映射回世界坐标

世界坐标轴屏幕中心位于 $(0,0,-1)$



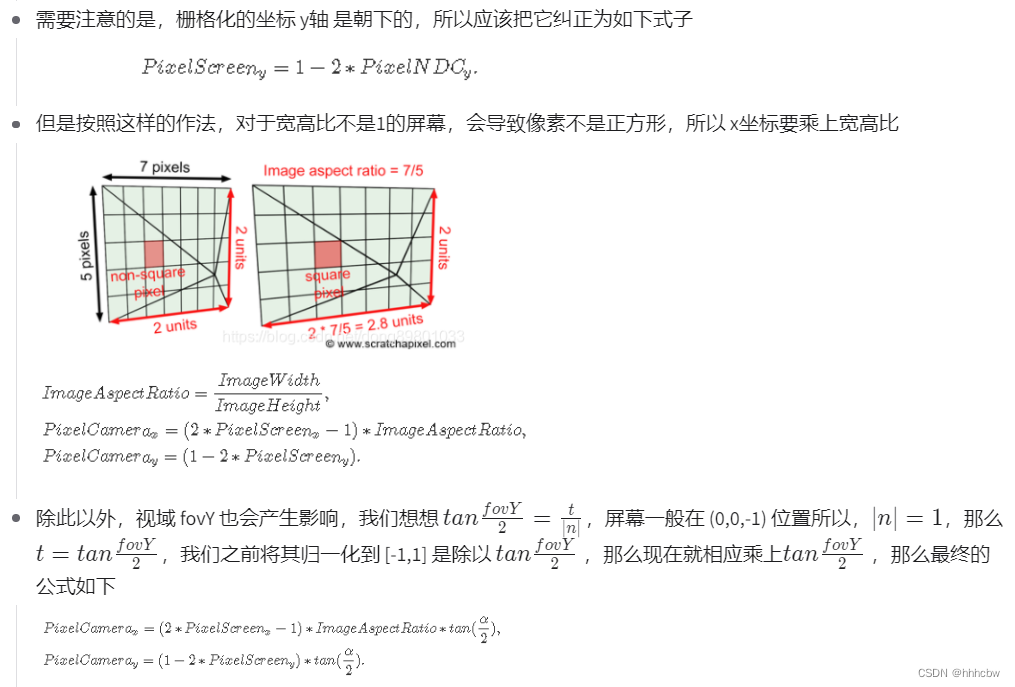
因此这里对应获得 x 和 y 的代码为

float x = (2.0f*(float(i)+0.5f)/scene.width-1.0f)*scale*imageAspectRatio;
float y = (1.0f-2.0f*(float(j)+0.5f)/scene.height)*scale;
1
2

判断光线与物体的交点

球体

光线与球体交点的过程与公式如下（就是光线方程代入球体方程得出）



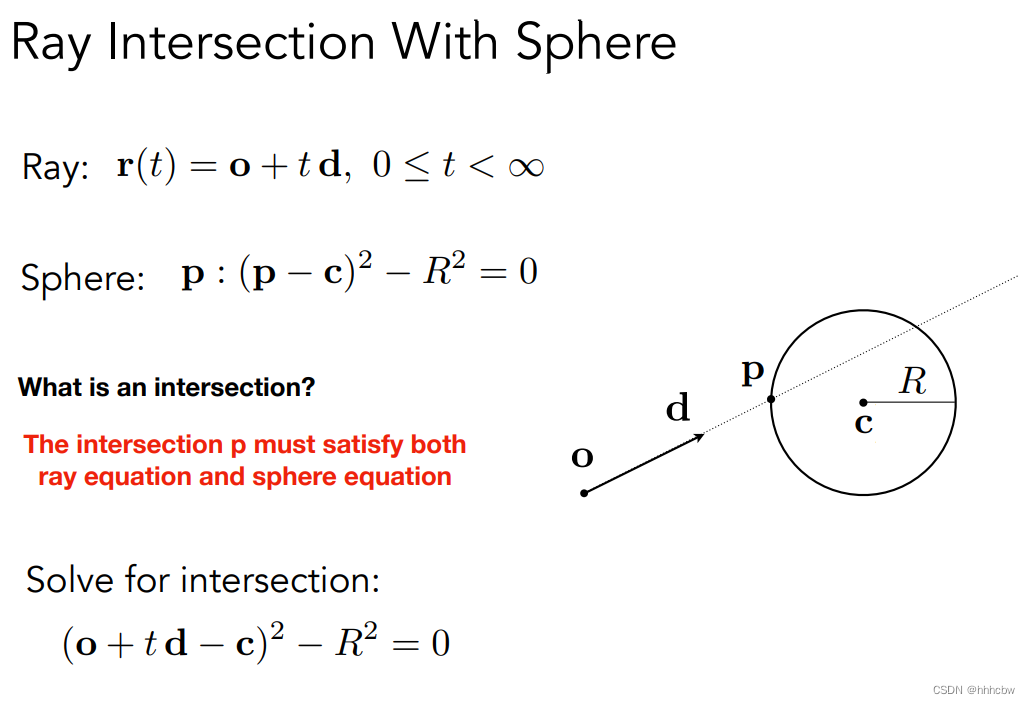
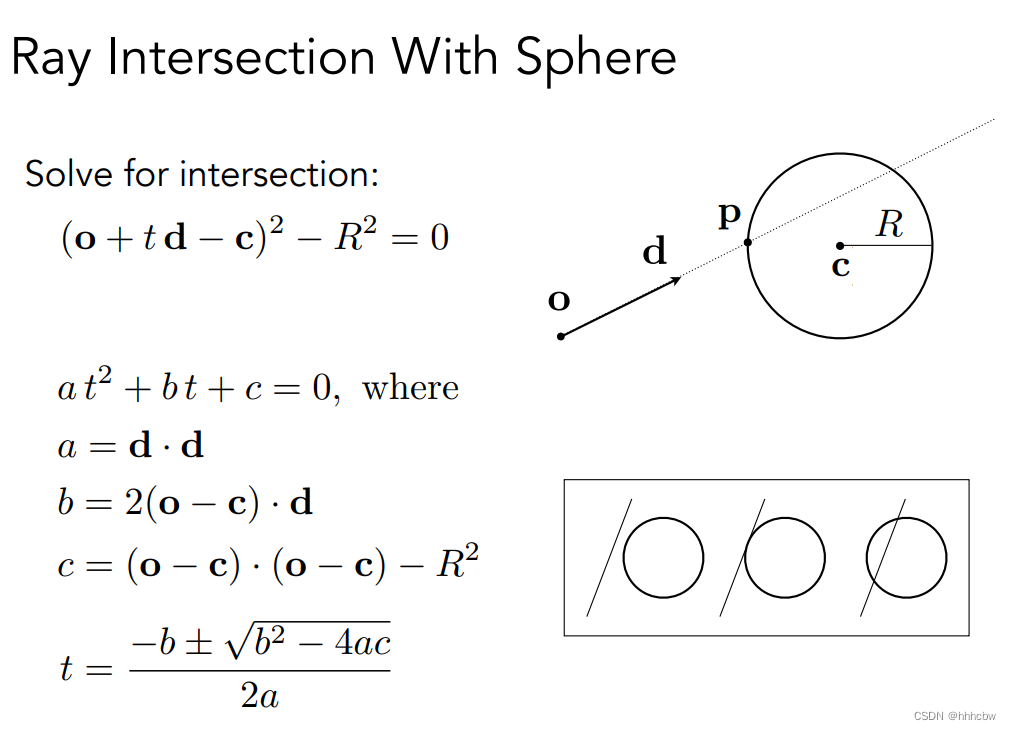
其代码如下

bool intersect(const Vector3f& orig, const Vector3f& dir, float& tnear, uint32_t&, Vector2f&) const override
    {
        // analytic solution
        Vector3f L = orig - center;
        float a = dotProduct(dir, dir);
        float b = 2 * dotProduct(dir, L);
        float c = dotProduct(L, L) - radius2;
        float t0, t1;
        if (!solveQuadratic(a, b, c, t0, t1))
            return false;
        if (t0 < 0)
            t0 = t1;
        if (t0 < 0)
            return false;
        tnear = t0;

        return true;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

三角形

判断光线与三角形是否有交点，一般先判断光线与三角形所在平面是否有交点，在判断交点是否在三角形内部。这里使用的 Möller Trumbore Algorithm可以更快判断光线与三角形交点，其公式如下，具体推导可以看这篇文章
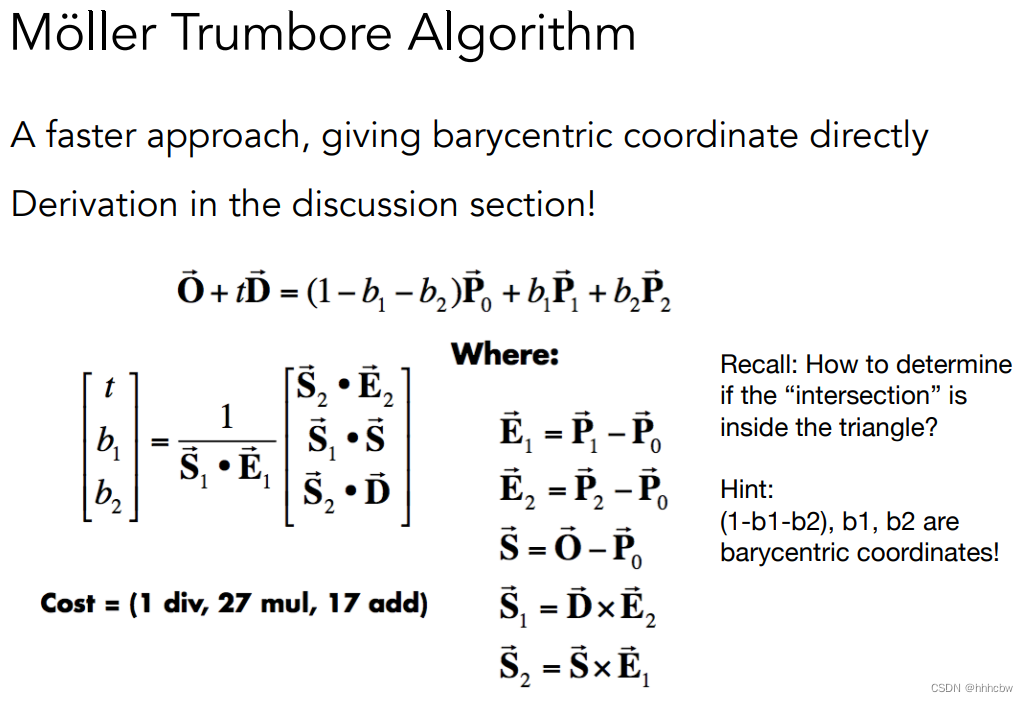
其代码如下，注意最后判断是否在三角形内的条件(前提不能在射线后面，即tnear>0)

bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
                          const Vector3f& dir, float& tnear, float& u, float& v)
{
    // TODO: Implement this function that tests whether the triangle
    // that's specified bt v0, v1 and v2 intersects with the ray (whose
    // origin is *orig* and direction is *dir*)
    // Also don't forget to update tnear, u and v.
    Vector3f E1 = v1 - v0;
    Vector3f E2 = v2 - v0;
    Vector3f S = orig - v0;
    Vector3f S1 = crossProduct(dir, E2);
    Vector3f S2 = crossProduct(S, E1);
    float n = 1.0f/dotProduct(S1, E1);
    Vector3f res(dotProduct(S2,E2),dotProduct(S1,S),dotProduct(S2,dir));
    res = n*res;
    tnear = res.x;
    u = res.y;
    v = res.z;
    if(tnear > 0.f && 1-u-v>=0.f && u>=0.f && v>=0.f)    
        return true;
    else  
        return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

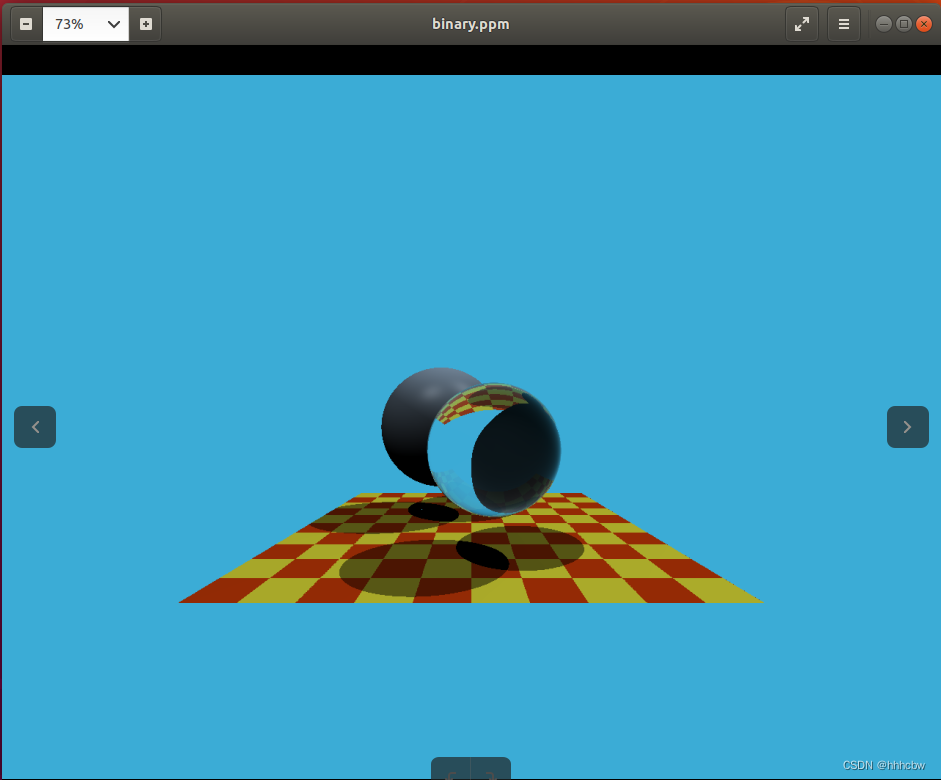
最终的运行结果如下