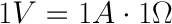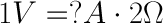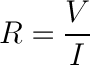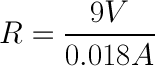创意电子学-小知识：电压、电流、电阻和欧姆定律

电压、电流、电阻和欧姆定律

原文地址

电基础知识

在开始探索电和电子世界时，从了解电压，电流和电阻的基础知识开始至关重要。这些是操纵和利用电所需的三个基本组成部分。起初，这些概念可能很难理解，因为我们无法“看到”它们。人们无法用肉眼看到流经电线的能量或放在桌子上的电池的电压。即使是天空中的闪电，虽然可见，但并不是真正的从云层到地球的能量交换，而是空气中对通过它的能量的反应。为了检测这种能量转移，我们必须使用万用表、频谱分析仪和示波器等测量工具来可视化系统中电荷的变化。但是，不用担心，本教程将为您提供有关电压，电流和电阻的基本了解以及这三者之间的关系。

格奥尔格·欧姆

本教程介绍

• 电荷与电压、电流和电阻的关系。
• 什么是电压、电流和电阻。
• 欧姆定律是什么，以及如何用它来理解电。
• 一个简单的实验来演示这些概念。

推荐阅读

• 什么是电
• 什么是电路？

电荷

电是电子的运动。电子产生电荷，我们可以利用电荷来做功。你的灯泡，你的立体声，你的手机，等等，都在利用电子的运动来做工作。它们都使用相同的基本电源：电子的运动。

本教程的三个基本原理可以用电子来解释，或者更具体地说，它们产生的电荷：

• 电压是两点之间的电荷差。
• 电流是电荷流动的速率。
• 电阻是材料抵抗电荷流动（电流）的倾向。

所以，当我们谈论这些值时，我们实际上是在描述电荷的运动，从而描述电子的行为。电路是一个闭环，允许电荷从一个地方移动到另一个地方。电路中的组件允许我们控制此电荷并使用它来完成工作。

格奥尔格·欧姆是一位研究电的巴伐利亚科学家。欧姆首先描述了由电流和电压定义的电阻单位。所以，让我们从电压开始，然后从那里开始。

电压

我们将电压定义为电路上两点之间的势能量。一个点比另一个点有更多的电荷。两点之间的电荷差称为电压。它是以伏特为单位测量的，从技术上讲，这是两点之间的势能差，每通过它的一库仑电荷将产生一焦耳的能量。单位“伏特”以意大利物理学家亚历山德罗·沃尔塔的名字命名，他发明了被认为是第一个化学电池的东西。电压在方程式和原理图中用字母“V”表示。

在描述电压、电流和电阻时，一个常见的类比是水箱。在这个类比中，电荷由水量表示，电压由水压表示，电流由水流表示。所以对于这个类比，请记住：

• 水 = 电荷
• 压力 = 电压
• 流量 = 电流

考虑一个高出地面一定高度的水箱。在这个水箱的底部有一个软管。

软管末端的压力可以表示电压。水箱中的水代表电荷。水箱中的水越多，电荷越高，软管末端测量的压力就越大。

我们可以把这个水塔想象成一个电池，一个我们存储一定量能量然后释放它的地方。如果我们将水箱排掉一定量，软管末端产生的压力就会下降。我们可以认为这是降低电压，就像当手电筒随着电池电量耗尽而变暗一样。流经软管的水量也会减少。压力越小，流水就越少，这让我们流淌到水流。

电流

我们可以将水箱中流经软管的水量视为电流。压力越高，流量越高，反之亦然。对于水，我们将测量一定时间内流经软管的水的体积。通过电，我们测量一段时间内流经电路的电荷量。电流以安培为单位进行测量（通常简称为“安培”）。安培定义为每秒6.241 * 10 ¹⁸个电子（1库仑）通过电路中的点。安培在等式中用字母“I”表示。

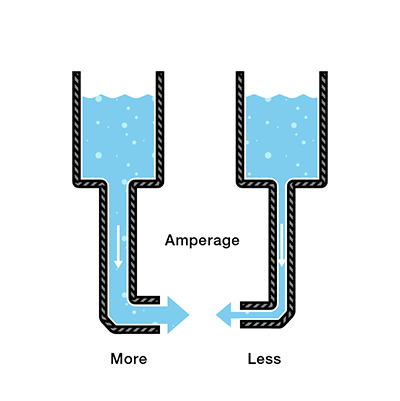
现在假设我们有两个水箱，每个水箱都有一个来自底部的软管。每个水箱都有完全相同的水量，但一个水箱上的软管比另一个水箱上的软管窄。

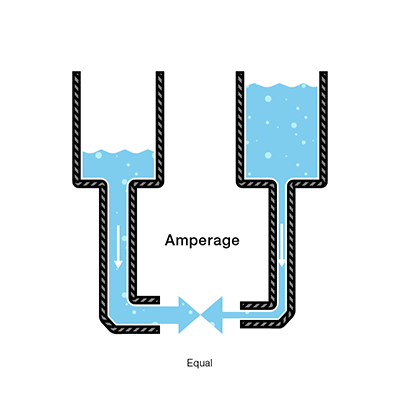
我们在任一软管的末端测量相同的压力量，但是当水开始流动时，使用较窄的软管的水箱中的水的流速将小于使用较宽的软管的水箱中的水的流速。在电气术语中，通过较窄软管的电流小于通过较宽软管的电流。如果我们希望通过两个软管的流量相同，则必须使用较窄的软管增加水箱中的水量（电荷）。

这增加了较窄软管末端的压力（电压），从而将更多的水推入水箱。这类似于电压增加导致电流增加。

现在我们开始看到电压和电流之间的关系。但这里需要考虑第三个因素：软管的宽度。在这个类比中，软管的宽度就是电阻。这意味着我们需要在模型中添加另一个项：

• 水 = 电荷（以库仑为单位测量）
• 压力 = 电压（以伏特为单位测量）
• 流量 = 电流（以安培或简称“安培”为单位测量）
• 软管宽度 = 电阻

电阻

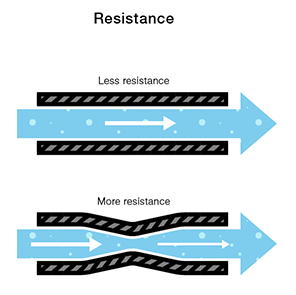
再想想我们的两个水箱，一个有窄管，一个有宽管。

按理说，在相同的压力下，我们无法通过狭窄的管道容纳比较宽的管道更多的体积。这就是阻力。窄管“抵抗”水流通过它，即使水与具有较宽管道的水箱处于相同的压力。

在电气术语中，这由两个具有相同电压和不同电阻的电路表示。具有较高电阻的电路将允许较少的电荷流动，这意味着具有较高电阻的电路流过它的电流较少。

这让我们回到了格奥尔格·欧姆。欧姆将“1欧姆”的电阻单位定义为导体中两点之间的电阻，其中施加1伏将推动1安培，或6.241×10 ¹⁸电子。该值通常用希腊字母“Ω”（称为omega）表示，发音为“ohm”。

欧姆定律

结合电压、电流和电阻等元素，欧姆开发了以下公式：

• V = 电压（以伏特为单位）
• I = 电流（以安培为单位）
• R = 电阻（以欧姆为单位）

这被称为欧姆定律。例如，假设我们有一个电位为1伏，电流为1安培，电阻为1欧姆的电路。使用欧姆定律，我们可以说：

假设这代表了我们的水箱带有宽软管。水箱中的水量定义为1伏，软管的“窄度”（流动阻力）定义为1欧姆。使用欧姆定律，这给了我们1安培的流量（电流）。

使用这个类比，现在让我们看一下带有窄软管的油箱。由于软管较窄，因此其流动阻力较高。让我们将此电阻定义为 2 欧姆。水箱中的水量与其他水箱相同，因此，使用欧姆定律，我们对带有窄软管的水箱的方程是

但目前的情况如何呢？因为电阻更大，电压相同，这给了我们0.5安培的电流值：

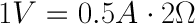
因此，油箱中的电流较低，电阻较高。现在我们可以看到，如果我们知道欧姆定律的两个值，我们就可以求解第三个值。让我们通过实验来证明这一点。

欧姆定律实验

对于此实验，我们希望使用9伏电池为LED供电。LED是脆弱的，在烧坏之前只能有一定量的电流流过它们。在 LED 的文档中，始终会有一个“额定电流”。这是在特定LED烧坏之前可以流过的最大电流。

所需材料

为了执行本教程末尾列出的实验，您需要：

• 万用表
• 9 伏电池
• 560欧姆电阻（或下一个最接近的值）
• 发光二极管

**注意：**LED是所谓的“非欧姆”设备。这意味着流经LED本身的电流方程并不像V=IR那么简单。LED在电路中引入一种称为“压降”的东西，从而改变流经它的电流量。然而，在这个实验中，我们只是试图保护LED免受过流的影响，因此我们将忽略LED的电流特性，并使用欧姆定律选择电阻值，以确保通过LED的电流安全地低于20mA。

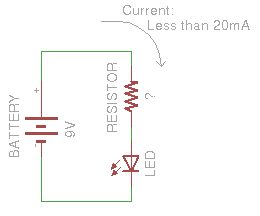
对于此示例，我们有一个 9 伏电池和一个额定电流为 20 毫安或 0.020 安培的红色 LED。为了安全起见，我们宁愿不以最大电流驱动LED，而是将其建议电流驱动，该电流在其数据表中列为18mA或0.018 A。如果我们简单地将LED直接连接到电池，欧姆定律的值如下所示：

因此：

由于我们还没有抵抗力：

除以零会给我们无限的电流！好吧，在实践中不是无限的，而是电池可以提供的电流。由于我们不希望有那么多电流流过我们的LED，因此我们需要一个电阻器。我们的电路应该如下所示：

我们可以以完全相同的方式使用欧姆定律来确定将给我们提供所需电流值的重磁器值：

因此：

带入公式：

解决阻力问题：

因此，我们需要一个大约500欧姆的电阻值，以将通过LED的电流保持在最大额定电流以下。

500欧姆不是现成电阻器的常用值，因此该器件使用560欧姆电阻器代替。以下是我们的设备组合在一起的样子。

成功！我们选择的电阻值足够高，可以将通过LED的电流保持在最大额定值以下，但又要足够低，使电流足以保持LED的美观和明亮。

这种LED/限流电阻器的例子在业余爱好电子产品中很常见。您经常需要使用欧姆定律来改变流过电路的电流量。这种实现的另一个例子是在莉莉帕德LED板中看到的。

通过这种设置，不必为LED选择电阻器，而是电阻器已经与LED一起板载，因此无需手动添加电阻器即可完成限流。

LED 之前或之后的电流限制？

为了使事情变得更加复杂，您可以将限流电阻放在LED的任一侧，其工作原理也一样！

许多第一次学习电子学的人都在努力思考这样一种观点，即限流电阻器可以位于LED的任一侧，电路仍将照常工作。

想象一下，一条连续循环中的河流，一条无限的，圆形的，流动的河流。如果我们要在其中设置一个水坝，整个河流将停止流动，而不仅仅是一侧。现在想象一下，我们在河里放了一个水车，它减缓了河水的流动。无论水车放在圆圈中的哪个位置，它仍然会减慢整个河流的流量。

这是一种过度简化，因为限流电阻不能放置在电路中的任何位置。它可以放置在LED的任一侧以执行其功能。

为了获得更科学的答案，我们转向基尔霍夫电压定律。正是由于这个定律，限流电阻可以放在LED的任一侧，并且仍然具有相同的效果。有关更多信息和使用KVL的一些练习问题，请访问此网站。

资源和进一步发展

现在，您应该了解电压，电流，电阻的概念以及这三者之间的关系。祝贺！用于分析电路的大多数方程和定律可以直接从欧姆定律中推导出来。通过了解这个简单的定律，您就了解了作为分析任何电路基础的概念！

有兴趣了解更多基础主题吗？

请参阅我们的**工程基础**页面，了解有关电气工程基石主题的完整列表。

带我去那里！

这些概念只是冰山一角。如果您希望进一步研究欧姆定律的更复杂的应用和电路设计，请务必查看以下教程。

• 串联与并联电路
• 电
• 模拟电路与数字电路
• 电阻
• 发光二极管
• 如何使用万用表