Java数据结构：稀疏数组的实现与应用

---

1 稀疏数组引入

1.1 使用场景

笔者在课程设计中曾写过一个扫雷小游戏，为了便于讲解，我们来做个简化（实际比这个复杂），只考虑当前位置有雷与无雷两种状况：雷用1表示，非雷用0表示。则将当前状态用二维数组表示如下：

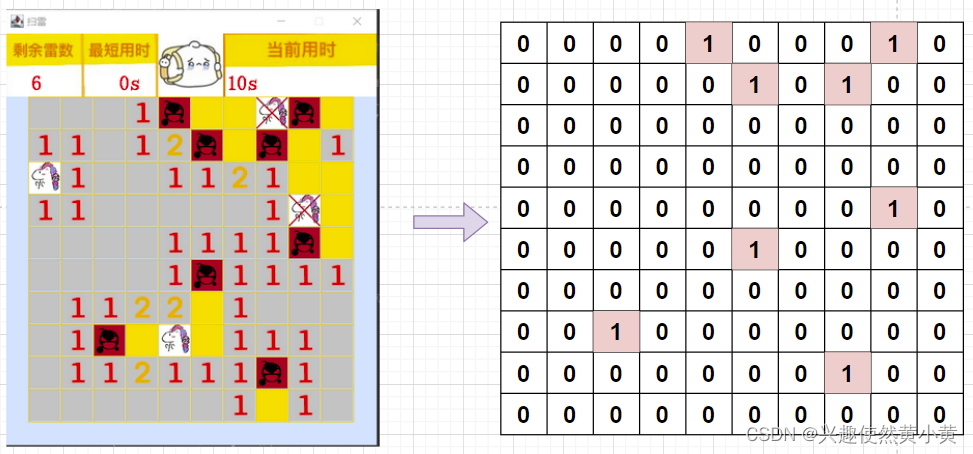
在右侧的二维数组中，很多都是0，即记录了很多没有意义的数据，因此，我们考虑使用稀疏数组进行存储结构的优化。

1.2 稀疏数组简介

当一个数组中的大部分元素都是0（或者为相同的某一值），可以考虑使用稀疏数组来优化保存。
而稀疏数组的基本处理方式为：

• 记录数组有几行几列，有几个有效值；
• 把有效值的元素的行、列及值记录在一个小规模的数组中，从而缩小程序的规模。

例如上述的二维数组用稀疏数组表示，可以创建一个n*3列的稀疏数组。其中，n为有效值个数加1，第一行用于存储二维数组的行数、列数及有效值的个数，便于恢复二维数组时使用。
而从第二行开始后的每一行，都记录某个有效值的所在行、列索引与值。
上述二维数组用稀疏数组表示如下：

• 以索引0那行，10 10 8为例：表示原二维数组有10行10列，共有8个有效值。
• 以索引1那行，0 4 1为例：即第一个有效值在原数组的第0行第4列（索引为0和4），值为1，以此类推…

---

2 稀疏数组的实现

2.1 案例概述

1.使用稀疏数组来保存前面1.1样例中的二维数组（见下图）；
2.可以由稀疏数组恢复成二维数组。

2.2 思路分析

二维数组转稀疏数组：

1. 遍历原始的二维数组，得到有效数据的个数 amount；
2. 根据 amount 可以创建稀疏数组 sparseArray[amount+1][3];
3. 将二维数组中的有效值存入稀疏数组中。

稀疏数组恢复二维数组：

1. 先读取稀疏数组的第一行，根据第一行的数据，创建原始二维数组；
2. 读取第二行及以后行的数据，按照每行的行、列、值恢复有效值，录入二维数组中。

2.3 代码实现

根据如上思路，逐步实现稀疏数组，详情可见代码注释

参考代码：

/**
 * @author 兴趣使然黄小黄
 * @version 1.0
 * 二维数组转稀疏数组、稀疏数组还原二维数组的实现
 */
public class SparseArray {

    public static void main(String[] args) {
        //先创建原始二维数组
        int[][] originalArray = new int[10][10];
        originalArray[0][4] = 1;
        originalArray[0][8] = 1;
        originalArray[1][5] = 1;
        originalArray[1][7] = 1;
        originalArray[4][8] = 1;
        originalArray[5][5] = 1;
        originalArray[7][2] = 1;
        originalArray[8][7] = 1;
        //输出原始的二维数组
        System.out.println("原始的二维数组:");
        for (int[] row: originalArray) {
            for (int data : row) {
                System.out.printf("%d\t", data);
            }
            System.out.println();
        }

        //将二维数组转成稀疏数组
        //1.遍历二维数组，得到非0的有效数据的个数
        int amount = 0;
        for (int i = 0; i < originalArray.length; i++) {
            for (int j = 0; j < originalArray[i].length; j++) {
                if (originalArray[i][j] != 0){
                    amount++;
                }
            }
        }
        System.out.println("amount = " + amount);
        //2.创建对应的稀疏数组 sparseArray[amount+1][3], 并初始化稀疏数组第一行的数据
        //第一行第一列: 原数组的行数   第一行第二列: 原数组的列数  第一行第三列: 原数组的有效数据个数
        int[][] sparseArray = new int[amount + 1][3];
        sparseArray[0][0] = 10;
        sparseArray[0][1] = 10;
        sparseArray[0][2] = amount;
        //3.遍历二维数组,将非0值存储进稀疏数组
        int count = 0; //用于记录是第几个非零数据
        for (int i = 0; i < originalArray.length; i++) {
            for (int j = 0; j < originalArray[i].length; j++) {
                if (originalArray[i][j] != 0){
                    count++;
                    sparseArray[count][0] = i; //记录所在行
                    sparseArray[count][1] = j; //记录所在列
                    sparseArray[count][2] = originalArray[i][j]; //记录值
                }
            }
        }
        //输出稀疏数组
        System.out.println("稀疏数组:");
        for (int i = 0; i < sparseArray.length; i++) {
                System.out.printf("%d\t%d\t%d\n", sparseArray[i][0], sparseArray[i][1], sparseArray[i][2]);
        }

        //将稀疏数组恢复成为二维数组
        //1.根据稀疏数组的第一行初始化二维数组
        int[][] recoveredArray = new int[sparseArray[0][0]][sparseArray[0][1]];
        //2.读取稀疏数组的后面行数据，赋值给原始二维数组
        for (int i = 1; i < sparseArray.length; i++) {
            recoveredArray[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];
        }
        //输出二维数组
        System.out.println("恢复后的二维数组:");
        for (int[] row: recoveredArray) {
            for (int data : row) {
                System.out.printf("%d\t", data);
            }
            System.out.println();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

运行结果：

原始的二维数组:
0	0	0	0	1	0	0	0	1	0	
0	0	0	0	0	1	0	1	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	1	0	
0	0	0	0	0	1	0	0	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	1	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	1	0	0	
0	0	0	0	0	0	0	0	0	0	
amount = 8
稀疏数组:
10	10	8
0	4	1
0	8	1
1	5	1
1	7	1
4	8	1
5	5	1
7	2	1
8	7	1
恢复后的二维数组:
0	0	0	0	1	0	0	0	1	0	
0	0	0	0	0	1	0	1	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	0	1	0	
0	0	0	0	0	1	0	0	0	0	
0	0	0	0	0	0	0	0	0	0	
0	0	1	0	0	0	0	0	0	0	
0	0	0	0	0	0	0	1	0	0	
0	0	0	0	0	0	0	0	0	0	
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

比对结果如下：

经过比较，恢复后的二维数组与原二维数组保持一致！
分析可知：原二维数组需要的空间为：10 * 10 *（int），而稀疏数组只需要 9 * 3 * (int)，相对节省了73(int)的空间！

---

写在最后

 本文被 Java数据结构 收录点击订阅专栏 ， 持续更新中。
 创作不易，如果你有任何问题，欢迎私信，感谢您的支持！