-
simple-HGN 介绍 - 一种简单有效的异构图建模方法
参考论文:http://keg.cs.tsinghua.edu.cn/jietang/publications/KDD21-Lv-et-al-HeterGNN.pdf
KDD 2021论文
这里只是把作者提出的这个模型拿出来介绍了!!!
目录
受简单 GAT 相对于高级专用异构 GNN 的优势的启发,作者提出了 Simple-HGN,这是一种简单有效的异构图建模方法。
Simple-HGN 采用 GAT 作为主干,对三种众所周知的技术进行了重新设计:可学习的边类型嵌入、残差连接和输出嵌入的 L2 归一化。图 1 说明了使用 Simple-HGN 的完整pipeline;紫色部分是 Simple-HGN 中对 GAT 的改进。
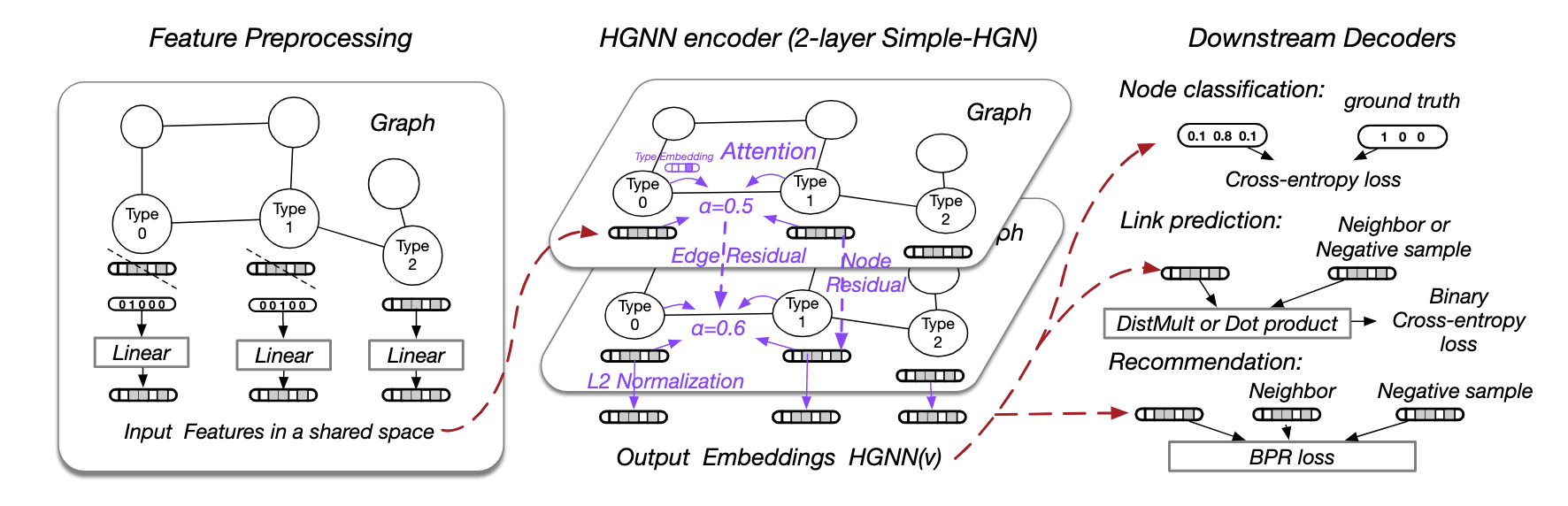
1 可学习的边类型嵌入
GAT缺陷:虽然 GAT 在建模同构图方面具有强大的能力,但由于忽略了节点或边的类型,它对于异构图可能不是最优的。
方法概括:为了解决这个问题,作者通过将边类型信息包含到注意力计算中来扩展原始的图注意力机制;
具体来说:(1)在每一层,作者为每个边类型
分配
维嵌入
;
(2)并使用边类型嵌入和节点嵌入来计算注意力分数,如下所示:

其中
表示节点和节点之间的边类型,而
是转换类型嵌入的可学习矩阵。
2 残差连接
前人研究:由于过度平滑和梯度消失问题,GNN 很难深入表示 [23, 38]。在计算机视觉中缓解这个问题的一个著名解决方案是残差连接[15]。然而,原始的 GCN 论文 [21] 在图卷积上显示了残差连接的否定结果。
最近的研究 [22] 发现,精心设计的预激活实现可以使 GNN 中的残差连接再次变得更好。
节点残差:作者为跨层的节点表示添加了预激活残差连接。
层的聚合可以表示为:
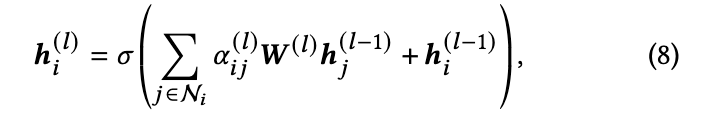
其中
是关于边
的注意力权重,
是一个激活函数(默认为 ELU)。当第l 层的维度发生变化时,需要额外的增加一个可学习线性变换
,即
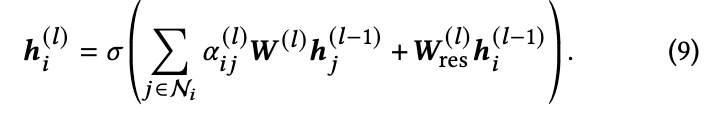
边残差: 最近,Realformer 揭示了注意力分数的残差连接也很有帮助。在通过等式(7)获得原始注意力分数之后,作者向它们添加残差连接:
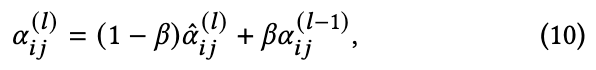
其中超参数
是缩放因子;
多头注意力:与 GAT 类似,作者采用多头注意力来增强模型的表达能力。具体来说,作者根据等式(8)执行独立的注意力机制,并将它们的结果连接起来作为最终表示。对应的更新规则为:
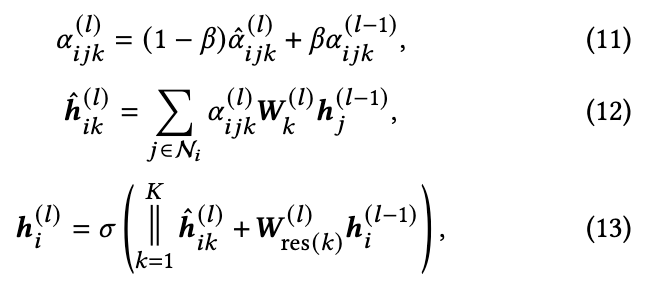
其中||表示连接操作,
是根据等式(9)通过
线性变换计算的注意力分数。
通常输出维度不能完全除以头数。
在 GAT 之后,作者不再使用连接,而是对最终 L层中的表示采用平均,即

适应链接预测:作者稍微修改了模型架构,以获得更好的链接预测性能。 边缘残差被移除,最终嵌入是所有层的嵌入的连接。这个改编版本类似于 JKNet[38]。
3 L2 归一化
作者发现输出嵌入的 L2 归一化非常有用,即

其中
是节点的输出嵌入,
是等式 (14) 的最终表示;
输出嵌入的归一化对于基于检索的任务来说非常常见,因为归一化后的点积将等同于余弦相似度。
优点:但作者也发现它对分类任务的改进,这在计算机视觉中也得到了观察 [26]。此外,它建议将缩放参数乘以输出嵌入[26]。作者现调整适当的值确实可以提高性能,但在不同的数据集中差异很大。因此为简单起见,保持方程式 (15) 的形式为简单起见。
-
相关阅读:
力扣打卡之链表反转
最小生成树之Kruskal、Prim
Java中List不同实现类的对比
瑞吉外卖项目 基于spring Boot+mybatis-plus开发 超详细笔记,有源码链接
数据结构:多栈共享技术
【Linux中的自旋锁、信号量、互斥体】通俗的解释
读书笔记——C++高性能编程(一至三)
【Turtle合集】火遍抖音的五款魔法阵终于被我找到了(初代萌王,童年的小樱回来了)
【MySQL从入门到精通】【高级篇】(十)MyISAM的索引方案&&索引的优缺点
Lib文件和netlist的关系,DDC文件和netlist的区别
- 原文地址:https://blog.csdn.net/qq_40671063/article/details/127422851