排序算法复习 | 插入排序(直接插入排序、希尔排序)与选择排序(直接选择排序、堆排序)

目录

插入排序

直接插入排序 

希尔排序 

选择排序 

直接选择排序 

堆排序 

---

插入排序

插入排序就是将一个记录插入到已经排好序的一个有序序列中，从而得到一个新的、有序的序列

直接插入排序 

把待排序的记录按其关键码值的大小逐一插入到一个已排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列. 

例如一个序列，{1，5，2，4，3}，按照升序进行排序.

开始时有序序列{1}，待排序记录{5，2，4，3}

第一趟排序后，有序序列 {1，5}，待排序记录{2，4，3}

第二趟排序后，有序序列 {1，2，5}，待排序记录{4，3}

....

最终结果，有序序列 {1，2，3，4，5}，待排序记录{}

import java.util.Arrays;
public class InsertSort {
    /**
     * 直接插入排序
     * 数据复杂度：最好O(n)  最坏O(n^2)
     * 空间复杂度：O(1)
     * 稳定的排序算法
     * @param arr
     */
    public static void insertSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int tmp = arr[i];
            int j = i - 1;
            for (; j >= 0; j--) {
                if (arr[j] > tmp) {
                    arr[j + 1] = arr[j];
                } else {
                    break;
                }
            }
            arr[j + 1] = tmp;
        }
    }
    public static void main(String[] args) {
        int[] arr = {1,3,4,7,6,2,7};
        insertSort(arr);
        System.out.println(Arrays.toString(arr));
    }
 
}

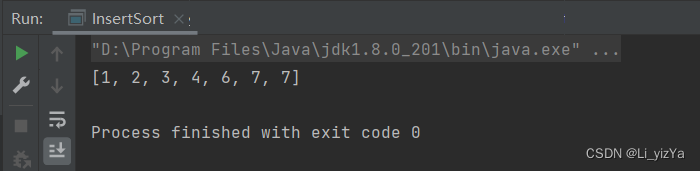
直接插入排序的空间复杂度为O(1)，时间复杂度最好情况下为数据有序的情况，时间复杂度为O(n)，最坏情况下时间复杂度为O(n^2). 

希尔排序 

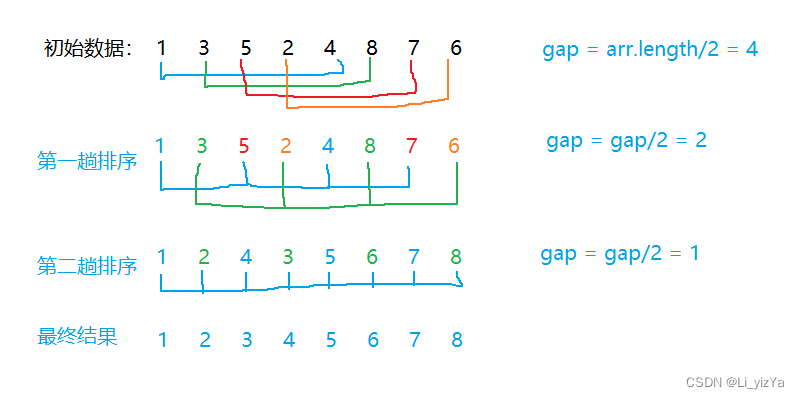
 希尔排序也是一种插入排序，它是直接插入排序改进后的一个更高效的版本，也称为缩小增量法，其基本思想是：先选定一个整数d，将待排序数组中所有记录分成组，所有距离为d的倍数的记录为同一个组，先在每个组内进行直接插入排序，然后取第二个增量，一直重复上述操作，当d=1时，所有记录有序.

 

import java.util.Arrays;
public class InsertSort {
    /**
     * 希尔排序
     * 时间复杂度：最好O(n)  最坏O(n^2)
     * 空间复杂度O(1)
     * 不稳定的排序算法
     * @param arr
     */
    public static void shellSort(int[] arr) {
        int n = 1;//记录排序次数
        int gap = arr.length;
        while (gap > 1) {
            gap /= 2;
            shell(arr, gap);
            System.out.println("第" + (n++) + "次排序结果为: " + Arrays.toString(arr));
        }
        shell(arr, 1);
    }
    public static void shell(int[] arr, int gap) {
        for (int i = gap; i < arr.length; i++) {
            int j = i - gap;
            int tmp = arr[i];
            for (; j >= 0; j -= gap) {
                if (arr[j] > tmp) {
                    arr[j + gap] = arr[j];
                } else {
                    break;
                }
            }
            arr[j + gap] = tmp;
        }
    }
    public static void main(String[] args) {
        int[] arr = {1,3,4,7,6,2,7};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

 

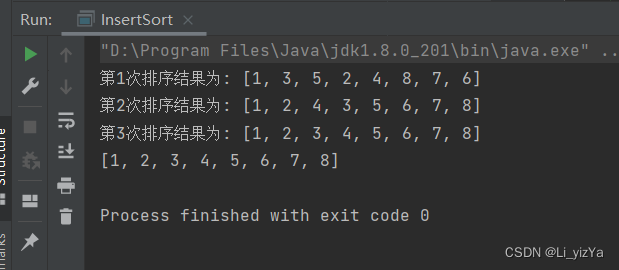
希尔排序的空间复杂度为O(1)，最好情况下时间复杂度为O(n)，最坏时间复杂度为O(n^2)，平均情况下时间复杂度为O(nlog2n)

选择排序 

直接选择排序 

每一次从待排序序列中选出一个最大(最小)的一个元素，存放到序列的起始位置，直至全部待排序的元素排列完毕 

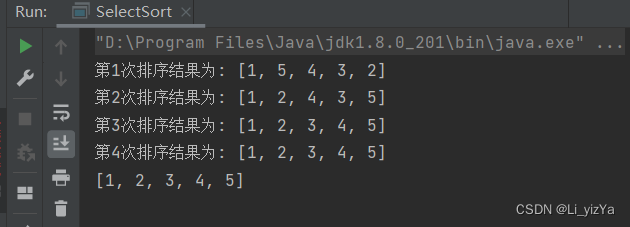
例如一个待排序序列{1，5，4，3，2}，排升序

第一次从待排序序列中选择一个最小的放在第一个位置{1，5，4，3，2}，第二次排序继续选择一个最小的放在第二个位置{1，2，4，3，5}，以此类推，最终得到一个排好序的序列

import java.util.Arrays;
 
public class SelectSort {
    /**
     * 直接选择排序
     * 时间复杂度：O(n^2)
     * 空间复杂度: O(1)
     * 不稳定的排序算法
     * @param arr
     */
    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length-1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            int tmp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = tmp;
            System.out.println("第" + (i+1) + "次排序结果为: " + Arrays.toString(arr));
        }
    }
    public static void main(String[] args) {
        int[] arr = {1, 5, 4, 3, 2};
        //int[] arr = {5,4,3,2,1};
        selectSort(arr);
        System.out.println(Arrays.toString(arr));
    }
 
}

堆排序 

 堆排序是指利用堆这种数据结构所设计的一种排序算法，它是选择排序的一种，它是通过堆来选择数据的。当要排升序的时候建立大根堆，排降序时建立小根堆.

例如要排升序：

 1.首先建立大根堆(若要排降序则建立小根堆)

2.将堆顶元素与堆最后一个元素进行交换，使末尾元素最大；

3.继续调整堆，再将堆顶元素与堆最后一个元素进行交换，得到第二大元素；

4.重复2和3，直至end == 0，排序结束.

 

import java.util.Arrays;
 
public class SelectSort {
    public static void main(String[] args) {
        int[] arr = {1, 5, 4, 3, 2};
        //int[] arr = {5,4,3,2,1};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void heapSort(int[] arr) {
        //创建大根堆，时间复杂度O(n)
        createHeap(arr);
        //排序
        int end = arr.length - 1;
        while (end > 0) {
            swap(arr, 0, end);
            shiftDown(arr, 0, end);
            end--;
        }
 
    }
    //创建大根堆
    private static void createHeap(int[] arr) {
        for (int parent = (arr.length-1-1) / 2; parent >= 0; parent--) {
            shiftDown(arr, parent, arr.length);
        }
    }
    //向下调整
    private static void shiftDown(int[] arr, int parent, int len) {
        int child = (2*parent) + 1;
        while (child < len) {
            if (child+1 < len && arr[child] < arr[child+1]) {
                child++;
            }
            if (arr[child] > arr[parent]) {
                swap(arr, child, parent);
                parent = child;
                child = 2*parent + 1;
            } else {
                break;
            }
        }
    }
    //交换元素
    private static void swap(int[] arr, int i, int end) {
        int tmp = arr[i];
        arr[i] = arr[end];
        arr[end] = tmp;
    }
 
}

堆排序的时间复杂度为O(n*logn)，空间复杂度为O(1)，是不稳定的排序算法