误差反向传播法原理

计算图

计算图将计算过程用图形表示出来。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。为了让大家熟悉计算图，先用计算图解一些简单的问题。从这些简单的问题开始，逐步深入，最终抵达误差反向传播法。问题如下：

太郎在超市买了2个苹果、3个橘子。其中，苹果每个100元，橘子每个150元。消费税是10%，请计算支付金额。

如图所示，构建了计算图后，从左向右进行计算。就像电路中的电流流动一样，计算结果从左向右传递。到达最右边的计算结果后，计算过程就结束了。从左向右进行计算”是一种正方向上的传播，简称为正向传播（forward propagation）。正向传播是从计算图出发点到结束点的传播。既然有正向传播这个名称，当然也可以考虑反向（从图上看的话，就是从右向左）的传播。实际上，这种传播称为反向传播（backward propagation）。反向传播将在接下来的导数计算中发挥重要作用。

链式法则

前面介绍的计算图的正向传播将计算结果正向（从左到右）传递，其计算过程是我们日常接触的计算过程，所以感觉上可能比较自然。而反向传播将局部导数向正方向的反方向（从右到左）传递，一开始可能会让人感到困惑。传递这个局部导数的原理，是基于链式法则（chain rule）的。

链式法则是关于复合函数的导数的性质，定义如下：如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。设有复合函数z=(x+y)²。该函数由如下两个函数复合而成：
∂ z/∂ x(z关于x的导数)可以用∂ z/∂ t(z关于t的导数)和∂ z/∂ x(t关于x的导数)的乘积表示：

而∂ t正好可以像下面这样“互相抵消”：

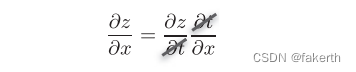
现在我们使用链式法则求函数的z=(x+y)²的导数。为此，我们要先求局部导数：


用计算图表示如下：

如图所示，计算图的反向传播从右到左传播信号。反向传播的计算顺序是，先将节点的输入信号乘以节点的局部导数，然后再传递给下一个节点。比如，反向传播时，上游传入“**2”节点的导数是∂ z/∂ z(也就是1)，将其乘以局部导数 （因为正向传播时输入是t、输出是z，所以这个节点的局部导数是∂ t/∂ t），然后传递给下一个节点。也就是说，反向传播是基于链式法则的。

反向传播

加法结点的反向传播

首先来考虑加法节点的反向传播。这里以z = x + y为对象，观察它的反向传播。z = x + y的导数可由下式（解析性地）计算出来：

如式所示， ∂ z/∂ x和∂ z/∂ y同时都等于1，用计算图表示：

反向传播将从上游传过来的导数∂ L/∂ z乘以1，然后传向下游。也就是说，因为加法节点的反向传播只乘以1，所以输入的值会原封不动地流向下一个节点。

乘法结点的反向传播

接下来，我们看一下乘法节点的反向传播。这里我们考虑z = x*y。这个式子的导数如下图所示：

用计算图表示如下：

乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系，正向传播时信号是x的话，反向传播时则是y；正向传播时信号是y的话，反向传播时则是x。另外，加法的反向传播只是将上游的值传给下游，并不需要正向传播的输入信号。但是，乘法的反向传播需要正向传播时的输入信号值。因此，实现乘法节点的反向传播时，要保存正向传播的输入信号。

简单层的实现

加法层的实现

层的实现中有两个共通的方法（接口）forward()和backward()。forward()对应正向传播，backward()对应反向传播。现在来实现加法层：

class AddLayer:
    def __init__(self):
        pass
    
    def forward(self, x, y):
        out = x + y
        return out
    
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy
1
2
3
4
5
6
7
8
9
10
11
12

加法层不需要特意进行初始化，所以__init__()中什么也不运行（pass语句表示“什么也不运行”）。加法层的forward()接收x和y两个参数，将它们相加后输出。backward()将上游传来的导数（dout）原封不动地传递给下游。

乘法层的实现

接下来，我们实现乘法层，乘法层作为MulLayer类，其实现过程如下所示：

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
    
    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y
        return out
    
    def backward(self, dout):
        dx = dout * self.y # 翻转x和y
        dy = dout * self.x
        return dx, dy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

init()中会初始化实例变量x和y，它们用于保存正向传播时的输入值。forward()接收x和y两个参数，将它们相乘后输出。backward()将从上游传来的导数（dout）乘以正向传播的翻转值，然后传给下游。

现在，我们使用加法层和乘法层，实现下图所示的购买2个苹果和3个橘子的例子：

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3)
price = mul_tax_layer.forward(all_price, tax)  # (4)
# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1)
print(price)  # 715
print(dapple_num, dapple, dorange, dorange_num, dtax)  # 110 2.2 3.3 165 650
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

这个实现稍微有一点长，但是每一条命令都很简单。首先，生成必要的层，以合适的顺序调用正向传播的forward()方法。然后，用与正向传播相反的顺序调用反向传播的backward()方法，就可以求出想要的导数。综上，计算图中层的实现（这里是加法层和乘法层）非常简单，使用这些层可以进行复杂的导数计算。下篇文章，我们来实现神经网络中使用的层。