自底向上的构建二叉堆

知识点

• 堆结构分为 大顶堆 和 小顶堆 。堆只能使用数组来构建，不能基于链表来实现。

• 堆( 二叉堆 )是完全二叉树结构。因此，若堆中父节点的索引为 i ，则左孩子节点的索引为 2*i + 1，右孩子节点的索引为 2*i + 2

• 大顶堆的 父节点的值 一定比 左右孩子节点的值 大。

  arr[i] >= arr[2*i + 1] && arr[i] >= arr[2*i + 2];
  1

• 小顶堆的 父节点的值 一定比 左右孩子节点的值 小。

  arr[i] <= arr[2*i + 1] && arr[i] <= arr[2*i + 2];
  1

自底向上建堆思路

1) 堆的构建需要从最后一个非叶子节点开始，采用自下而上、从右往左的顺序进行构建。

2) 最后一个非叶子节点的下标为 i = (array.length / 2) - 1;

// 构建堆（堆是在已有数组的基础上进行构建的）
private static void buildHead(int[] arr) {
    // 从最后一个非叶子结点开始
    for (int i = arr.length / 2 - 1; i >= 0; i--) {
        // 从最后一个非叶子结点自下而上，自左往右调整结构
        adjustHeap(arr, i, arr.length);
    }
}
1
2
3
4
5
6
7
8

3) 其中 adjustHeap() 方法的作用是用于调整子树的结构，保证以 i 为根节点的子树的父节点都比子节点大。

构建过程

第1轮：8 是最后一个非叶子节点，调用adjustHeap()方法进行调整，如果左右孩子的值比父节点的值大，则交换它们的位置。这里8比6和4大，所以不用交换位置。



第2轮：4 比 3 和 1 大，调用adjustHeap()方法时，不用交换位置。

第3轮：14 比 7 和 9 大，调用adjustHeap()方法时，不用交换位置。



第4轮：15 比 8 和 5 大，调用adjustHeap()方法时，不用交换位置。



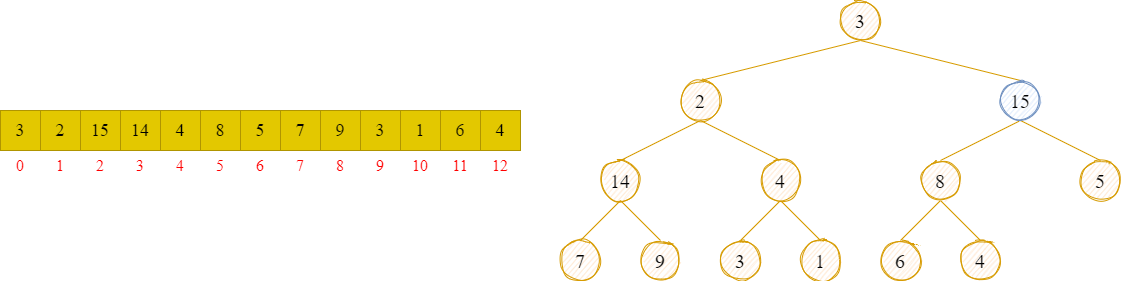
第5轮：2 比 14 和 4 小，调用adjustHeap()方法调整时，取左右孩子中最大的哪个同父节点交换位置。

• 但需要注意的是：这一轮并没有结束。因为交换了 2 和 14 的位置，导致父节点为 2 的子树不符合大顶堆的结构。
• 所以交换2 和 14的位置后，需要再次调用adjustHeap()方法，重新调整其结构( 交换 2 和 9 的位置，使其符合大顶堆结构 )。
  

第6轮：3 比 14 和 15 小，调用adjustHeap()方法调整时，取左右孩子中最大的哪个同父节点交换位置，即 3 和 15 交换位置。

• 这一轮并没有结束。交换了 3 和 15 的位置后，导致父节点为 3 的子树不符合大顶堆的结构。递归调用adjustHeap()进行调整（交换3 和 8 的位置）。

• 调整之后，父节点为 3 的子树还是不符合大顶堆的结构，继续递归调用adjustHeap()进行调整（交换3 和 6 的位置）。直至符合堆结构为止。

至此，堆构建完成。

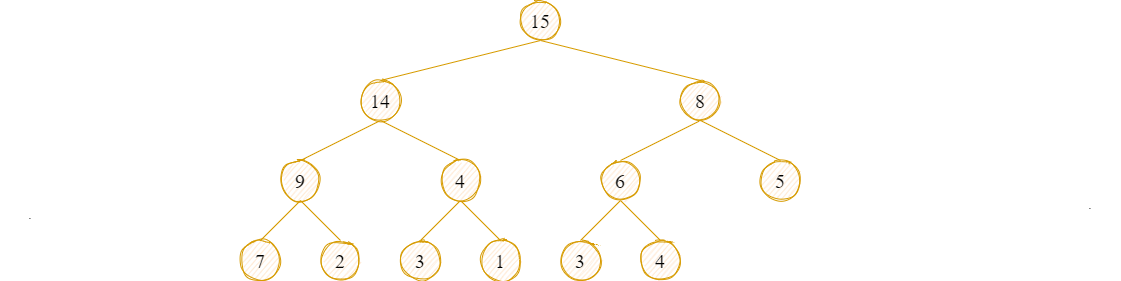
堆构建代码

import java.util.Arrays;

public class BuildHeap {

    public static void main(String[] args) {
        int[] array = new int[]{3, 2, 5, 7, 4, 8, 15, 9, 14};
        BuildHeap.buildHeap(array);
        System.out.println(Arrays.toString(array));  // 打印[15, 14, 8, 9, 4, 3, 5, 2, 7]
    }

    private static void buildHeap(int[] arr) {
        // 最后一个非叶子节点的索引
        int index = arr.length/2 - 1;

        // 从最后一个非叶子节点开始，自下往上、子右往左调整
        for (int i = index; i >= 0; i--) {
            adjustHeap(arr, i, arr.length);
        }
    }

    private static void adjustHeap(int[] arr, int i, int len){
        int left = 2*i + 1;  // i 节点左孩子的索引
        int right = 2*i + 2;  // i 节点右孩子的索引
        // 临时变量记录父节点与左右孩子节点中最大值的索引位置，初始时为父节点的索引
        int maxIndex = i;

        
        if(left < len && arr[left] > arr[maxIndex]){
            maxIndex = left;
        }

        if(right < len && arr[right] > arr[maxIndex]){
            maxIndex = right;
        }

        // 如果最大值不是父节点
        if(maxIndex != i){
            // 则交换父节点和最大值的的位置
            swap(arr, maxIndex, i);
            // 为保证交换节点位置后，导致索引为maxIndex的节点比其子节点的值小，从而不符合堆结构，所以递归调用adjustHeap()进行调整，具体原因看上述堆构建过程得到第 5 轮
            adjustHeap(arr, maxIndex, len);
        }
    }

    // 交换位置
    private static void swap(int[] arr, int a, int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

其中最关键的是下面这部分代码，对于初学者而言比较难理解。(作者开始的时候，也不是很理解为什么 swap() 交换节点位置后，还要跟着调用 adjustHeap()，这个问题在上面堆构建过程的第 5、6 轮有详细讲解)

 // 如果最大值不是父节点
if(maxIndex != i){
    // 则交换父节点和最大值的的位置
    swap(arr, maxIndex, i);
    // 为保证交换节点位置后，导致索引为maxIndex的节点比其子节点的值小，从而不符合堆结构，所以递归调用adjustHeap()进行调整，具体原因看上述堆构建过程得到第 5 轮
    adjustHeap(arr, maxIndex, len);
}
1
2
3
4
5
6
7

复杂度分析

• 构建堆的时间复杂度是$O(n)$

为什么自底向上建堆的时间复杂度是$O(n)$？

• 该建堆方式是从倒数第二层的最后一个非叶子节点开始，从右向左，从下到上的向下进行调整。

假设这个堆是满二叉树，共有 n 个节点，树高为h。

• 第一层有 1 个节点(根节点)，该结点最多向下进行 h - 1 次调整。
• 第二层有 2 个节点，每个节点最多向下进行 h - 2 次调整。
• 第三层有 4 个节点，每个节点最多向下进行 h - 3 次调整。
  .
  .
  .
• 第 h 层共有 $2^{h-1}$ 个节点，每个节点最多向下进行 h - h = 0 次调整。

T(n) = $2^0$ × (h - 1) + $2^1$ × (h - 2) + $2^2$ × (h - 3) + . . . + $2^{h-2}$ × 1 + $2^{h-1}$ × 0

     = $2^0$ × (h - 1) + $2^1$ × (h - 2) + $2^2$ × (h - 3) + . . . + $2^{h-2}$ × 1

根据错位相减法，左右两边同时乘以2：

2T(n) =                $2^1$ × (h - 1) + $2^2$ × (h - 2) + $2^3$ × (h - 3) + . . . + $2^{h-1}$ × 1
 T(n) = $2^0$ × (h - 1) + $2^1$ × (h - 2) + $2^2$ × (h - 3) + $2^3$ × (h - 4) + . . . + $2^{h-2}$ × 1

2T(n) - T(n) = -$2^0$ × (h - 1) + $2^1$ + $2^2$ + $2^3$ + . . . + $2^{h-1}$

             = $2^h$ - $2^1$ - $2^0$ × (h - 1)
             = $2^h$ - 1 - h

所以 T(n) = $2^h$ - 1 - h

因为满二叉树得总结点个数 n = $2^h$ - 1 个节点，树高 h = ${\log }_2^{n+1}$

所以自底向上建堆的最坏得时间复杂度为 T(n) = n - ${\log }_2^{n+1}$，即$O(n)$

堆有什么作用呢？

优先队列的底层是用小顶堆来实现的。