• 长短时记忆网络(Long Short Term Memory，LSTM)详解

      长短时记忆网络是循环神经网络(RNNs)的一种，用于时序数据的预测或文本翻译等方面。LSTM的出现主要是用来解决传统RNN长期依赖问题。对于传统的RNN，随着序列间隔的拉长，由于梯度爆炸或梯度消失等问题，使得模型在训练过程中不稳定或根本无法进行有效学习。与RNN相比，LSTM的每个单元结构——LSTM cell增加了更多的结构，通过设计门限结构解决长期依赖问题，所以LSTM可以具有比较长的短期记忆，与RNN相比具有更好的效果。

    一：基本原理

      关于LSTM，其整体结构与RNN基本完全相同，都是由多个cell串联起来，并且也有双向LSTM、深层LSTM，结构与RNN也完全相同。所以兔兔在这里不在赘述，需要了解的同学可以参考兔兔的上一篇循环神经网络(Recurrent Neural Network)详解。兔兔在下面着重讲述LSTM cell结构。

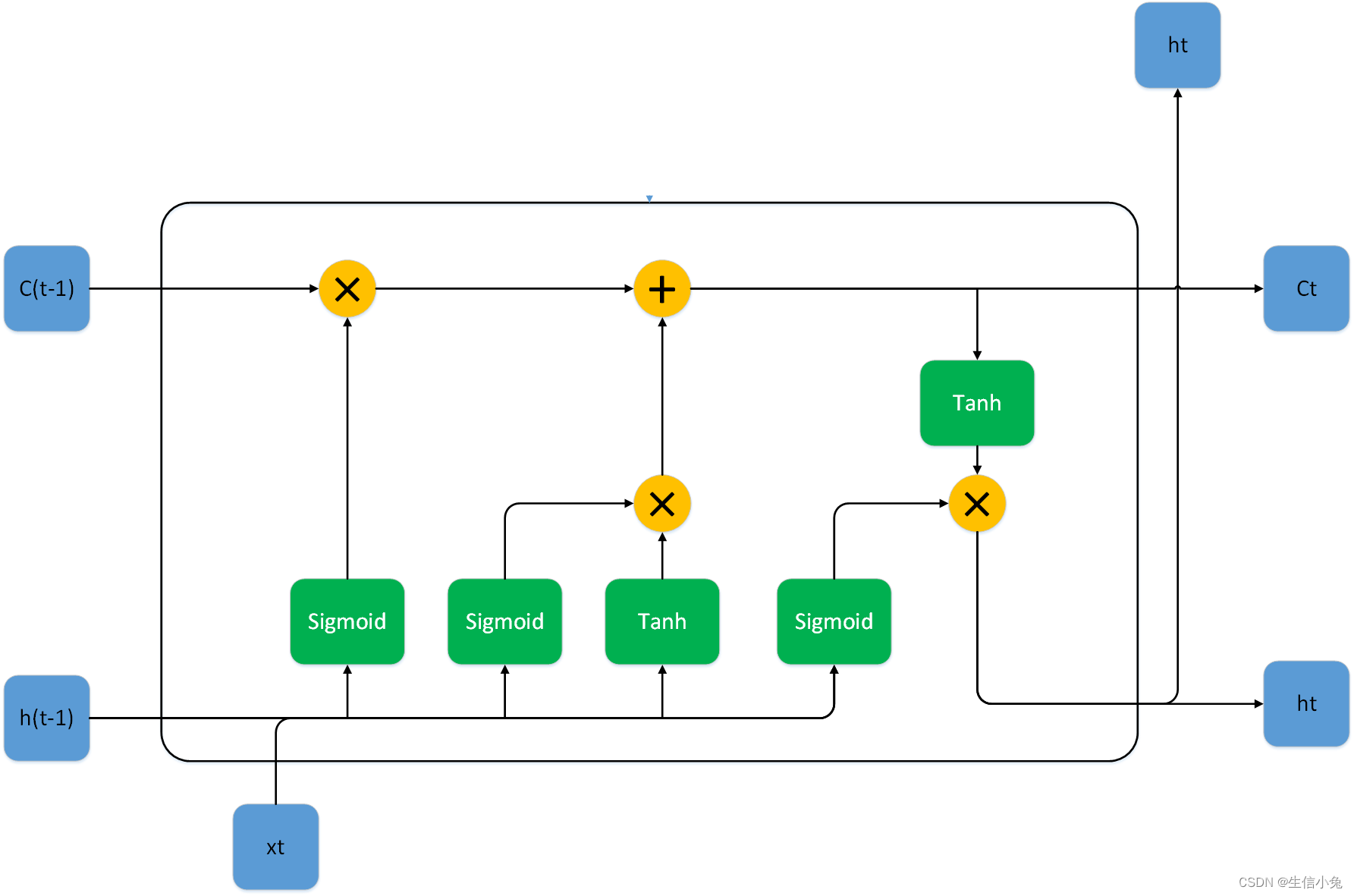
      上图为一个LSTM cell的整体结构，与RNN相比，我们发现在cell直间除了之前的隐藏状态ht,还多了一个Ct，并且内部结构也相对较为复杂。对于LSTM cell，内部分为三个部分：遗忘门(也称为保持门 keep gate)、输入门(也称为更新门update gate，写入门write gate)与输出门。

      （1）遗忘门(Forget Gate)

      在LSTM cell中，保持门用于控制记忆单元里那些信息舍弃(遗忘)或保留。设输入数据xt特征数量为p，则dim=(p,1)，h(t-1)的维度为dim=(q,1)，参数矩阵W_{if}的维度为dim=(q,p)，偏置b_{if}：dim=(q,1)，W_{hf}：dim=(q,q),偏置b_{hf}：dim=(q,1)。最终的输出ft为：

    f_t=sigmoid(W_{if}.x_t+b_{if}+W_{hf}.h_{t-1}+b_{hf})

      （2）输入门(Input Gate)

      输入门决定更新记忆单元的信息，包括Sigmoid与Tanh两个部分，它们两个都包含当前时刻的输入xt与上一时刻隐藏状态h(t-1)。Sigmoid部分的参数有W_{ii}、b_{ii}、W_{hi}、b_{hi}，dim分别为(q,p),(q,1),(q,q),(q,1)；Tanh部分的参数W_{ig}、b_{ig}、W_{hg}、b_{hg}，dim分别为(q,p),(q,1),(q,q),(q,1)。

      得到输入门的两个输出it、gt后，再由遗忘门得到的ft与上一时刻的状态C(t-1)进行计算，可以得到更新的状态Ct。

    i_t=sigmoid(W_{ii}.x_t+b_{ii}+W_{hi}.h_{t-1}+b_{hi}) \\g_t=tanh(W_{ig}.x_t+b_{ig}+W_{hg}.h_{t-1}+b_{hg})\\c_t=f_t*c_{t-1}+i*g_t

      这里的乘法"*"是两个向量对应位置相乘，准确来说是哈达玛乘积，一般也可以用\odot表示。而且这里ft、c(t-1)、it、gt、ct的维度都为(q,1)。

      （3）输出门(Output Gate)

       输出门的功能是读取刚刚更新过的神经网络状态，对记忆单元进行输出，而具体哪些信息可以输出受输出门的控制。

      输出层的参数有W_{io}、h_{io}、W_{ho}、b_{ho}。通过输出门得到ot，最终由ot与ct得到此时刻的输出ht，并且也可以继续传递到下一个cell。

    o_t=sigmoid(W_{io}.x_t+b_{io}+W_{ho}.h_{t-1}+b_{ho}) \\ h_t=o_t*tanh(c_t)

    LSTM与RNN同样权值共享，每一个LSTM cell都使用相同的参数。在这个模型中，所需要的参数有W_{if},W_{ii},W_{ig},W_{io},W_{hf},W_{hi},W_{hg},W_{ho}与b_{if},b_{ii},b_{ig},b_{io},b_{hf},b_{hi},b_{hg},b_{ho}，有时根据需要也可以不需要偏置b。

    二：方法实现

    1.使用Pytorch设计LSTMCell与LSTM

    1. import torch
    2. from torch import nn
    3. from torch.utils.data import DataLoader
    4. import numpy as np
    5. class LSTMCell(nn.Module):
    6.     def __init__(self,input_size,hidden_size):
    7.         '''
    8.         :param input_size: 输入特征个数
    9.         :param hidden_size: 隐藏层c、h的特征数
    10.         '''
    11.         super().__init__()
    12.         self.w_if=nn.Parameter(torch.randn(size=(input_size,hidden_size)))
    13.         self.w_ii=nn.Parameter(torch.randn(size=(input_size,hidden_size)))
    14.         self.w_ig=nn.Parameter(torch.randn(size=(input_size,hidden_size)))
    15.         self.w_io=nn.Parameter(torch.randn(size=(input_size,hidden_size)))
    16.         self.w_hf=nn.Parameter(torch.randn(size=(hidden_size,hidden_size)))
    17.         self.w_hi=nn.Parameter(torch.randn(size=(hidden_size,hidden_size)))
    18.         self.w_hg=nn.Parameter(torch.randn(size=(hidden_size,hidden_size)))
    19.         self.w_ho=nn.Parameter(torch.randn(size=(hidden_size,hidden_size)))
    20.         self.b_if=nn.Parameter(torch.randn(size=(1,hidden_size)))
    21.         self.b_ii=nn.Parameter(torch.randn(size=(1,hidden_size)))
    22.         self.b_ig=nn.Parameter(torch.randn(size=(1,hidden_size)))
    23.         self.b_io=nn.Parameter(torch.randn(size=(1,hidden_size)))
    24.         self.b_hf=nn.Parameter(torch.randn(size=(1,hidden_size)))
    25.         self.b_hi=nn.Parameter(torch.randn(size=(1,hidden_size)))
    26.         self.b_hg=nn.Parameter(torch.randn(size=(1,hidden_size)))
    27.         self.b_ho=nn.Parameter(torch.randn(size=(1,hidden_size)))
    28.         self.sigmoid=nn.Sigmoid()
    29.         self.tanh=nn.Tanh()
    30.     def forward(self,input,h,c):
    31.         ft=self.sigmoid(torch.matmul(input,self.w_if)+self.b_if+torch.matmul(h,self.w_hf)+self.b_hf)
    32.         it=self.sigmoid(torch.matmul(input,self.w_ii)+self.b_ii+torch.matmul(h,self.w_hi)+self.b_hi)
    33.         gt=self.tanh(torch.matmul(input,self.w_ig)+self.b_ig+torch.matmul(h,self.w_hg)+self.b_hg)
    34.         ct=torch.mul(ft,c)+torch.mul(it,gt)
    35.         ot=self.sigmoid(torch.matmul(input,self.w_io)+self.b_io+torch.matmul(h,self.w_ho)+self.b_ho)
    36.         ht=torch.mul(ot,self.tanh(ct))
    37.         return ht,ct
    38. class LSTM(LSTMCell):
    39.     def __init__(self,input_size,hidden_size):
    40.         super().__init__(input_size,hidden_size)
    41.         self.input_size=input_size
    42.         self.hidden_size=hidden_size
    43.         self.lstmcell=LSTMCell(input_size,hidden_size)
    44.     def forward(self,input):
    45.         b,l,h=input.shape
    46.         output=[]
    47.         h0=torch.zeros(size=(1,self.hidden_size))
    48.         c0=torch.zeros(size=(1,self.hidden_size))
    49.         for i in range(l):
    50.             ht,ct=self.lstmcell(input[:,i,:],h0,c0)
    51.             output.append(ht)
    52.             h0,c0=ht,ct
    53.         return torch.stack(output).permute(1,0,2),c0
    54.  
    55. a=np.arange(0,100,0.1)
    56. b=np.sin(a)
    57. data=[]
    58. label=[]
    59. for i in range(1000-20):
    60.     data.append(b[i:i+10].reshape(-1,1))
    61.     label.append(b[i+10:i+20].reshape(-1,1))
    62.  
    63. class dataset:
    64.     def __init__(self):
    65.         self.data=torch.tensor(np.array(data),dtype=torch.float32)
    66.         self.label=torch.tensor(np.array(label),dtype=torch.float32)
    67.         self.n=len(data)
    68.     def __len__(self):
    69.         return self.n
    70.     def __getitem__(self, item):
    71.         return self.data[item],self.label[item]
    72.  
    73. if __name__=='__main__':
    74.     lstm=LSTM(input_size=1,hidden_size=1)
    75.     optim=torch.optim.Adam(params=lstm.parameters())
    76.     Loss=nn.MSELoss()
    77.     data=DataLoader(dataset(),shuffle=True,batch_size=4)
    78.     for i in range(10):
    79.         for d in data:
    80.             yp=lstm(d[0])[0]
    81.             loss=Loss(yp,d[1])
    82.             optim.zero_grad()
    83.             loss.backward()
    84.             optim.step()
    85.             print(loss)

    2.使用Pytorch中LSTM方法

      Pytorch中LSTMCell与LSTM方法中参数与RNN方法中的参数完全一致，意义相同，并且也可以控制参数来设置双向LSTM、深层LSTM等模型，兔兔在这里不再赘述，需要的同学可以参考兔兔前面的文章。唯一不同的是，LSTMcell除了input 和h，还需要c。LSTM的输出除了所有LSTM cell的输出，还有最后一个cell的ct、ht的输出。

      兔兔在这里仍以Bitcoin数据为例，利用三个月的数据进行训练，从而能够进行未来数据的预测。这部分代码与之前RNN那里的代码几乎相同，只是把nn.RNN改成了nn.LSTM。

    1. import pandas as pd
    2. import numpy as np
    3. import re
    4. import torch
    5. from torch import nn
    6. from torch.utils.data import DataLoader
    7.  
    8. df=pd.DataFrame(pd.read_csv('Bitcoin.csv'))
    9. n=len(df)
    10. opening=[]
    11. closing=[]
    12. transaction=[]
    13. for i in range(n):
    14.       a = re.split(',',df['开盘'].loc[i])
    15.       a=float(a[0])*1000+float(a[1])
    16.       b = re.split(',', df['收盘'].loc[i])
    17.       b = float(b[0]) * 1000 + float(b[1])
    18.       c=re.split('K',df['交易量'].loc[i])[0]
    19.       c=float(c)
    20.       opening.append(a)
    21.       closing.append(b)
    22.       transaction.append(c)
    23. data=np.array([opening,closing,transaction]).transpose()
    24.  
    25. seq_size=10 #RNN长度
    26. train_num=1000#训练数据个数
    27. epoch=100
    28.  
    29. train_data=[]
    30. train_label=[]
    31. for i in range(1000):
    32.       j=np.random.randint(0,n-seq_size-2)
    33.       train_data.append(data[j:j+seq_size])
    34.       train_label.append(data[j+2:j+seq_size+2])
    35.  
    36. train_data=np.float32(np.array(train_data,dtype=object))
    37. train_label=np.float32(np.array(train_label,dtype=object))
    38. class dataset:
    39.       def __init__(self):
    40.           self.data=torch.tensor(train_data,dtype=torch.float32)
    41.           self.label=torch.tensor(train_label,dtype=torch.float32)
    42.       def __len__(self):
    43.           return train_num
    44.       def __getitem__(self, item):
    45.            return self.data[item],self.label[item]
    46.  
    47. lstm=nn.LSTM(input_size=3,hidden_size=3,bidirectional=False,batch_first=True,num_layers=2)
    48. optim=torch.optim.Adam(params=lstm.parameters(),lr=1e-12)
    49. Loss=nn.MSELoss()
    50. data=DataLoader(dataset(),batch_size=10)
    51.  
    52. for i in range(epoch):
    53.       print('the {} epoch'.format(i))
    54.       for d in data:
    55.             yp=lstm(d[0])[0]
    56.             loss=Loss(yp,d[1])
    57.             optim.zero_grad()
    58.             loss.backward()
    59.             optim.step()
    60.             print(loss.data)

    三：总结

      长短时记忆网络作为RNN的一种改进方法，在一定程度上克服了长期依赖问题，并且成为目前循环神经网络在实际应用中的常用模型之一。当然，该模型在更为复杂的问题上仍有一定的不足，所以在RNNs中仍有其它种类的循环神经网络，用以解决不同的问题。

  • 相关阅读:
    opencv c++ 霍夫圆检测
    【卷积神经网络】ResNets 残差网络
    从键盘任意输出一个整数n，若n不是素数，则计算并输出其所有因子（不包括1），否则输出该数为素数
    Vue学习笔记（七）：绑定css样式
    算法趣题-Q34
    Cisco Packet Tracer官网安装配置
    docker实战学习2022版本(八)之compose容器编排和轻量级可视化工具Portainer
    Linux系统上搭建Java的运行环境，并且部署JavaWeb程序
    计算机毕业设计之旅游分享网站
    Python3 运算符
  • 原文地址：https://blog.csdn.net/weixin_60737527/article/details/127129363