《算法导论》学习（十六）----一文讲懂红黑树

---

前言

本文将主要讲解红黑树，给出了红黑树复杂的插入删除操作的讲解

---

一、红黑树

1.什么是红黑树？

红黑树是一颗二叉搜索树，它在每个结点上增加了一个存储位来表示结点的颜色，可以是RED和BLACK。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似于平衡的。

想了解一般二叉搜索树的读者可以参考文章：
《算法导论》学习（十五）----二叉搜索树（C语言）

2.为什么需要红黑树？

二叉搜索树各个操作的期望时间复杂度是：
$O(lgn)=O(h),h是二叉搜索树的树高，有h=O(lgn)$

但是随着各个操作的进行，二叉搜索树可能会变得左右两边的树高相差严重，甚至在极端情况下，直接演变成一个链表。那么这时，二叉搜索树的时间复杂度就近似于$O(n)$了。

根据上面的分析，我们可以发现限制二叉搜索树的时间复杂度主要是二叉树左右高度的严重不平衡，我们称这种情况位“二叉搜索树的不平衡”。

那么我们就需要一种平衡的二叉搜索树，来保证运行时间的稳定性。那么红黑树就是这样一个“近似于平衡的二叉搜索树”。

3.为什么要用“近似平衡”而不是“高度平衡”？

一般来讲，高度平衡的二叉搜索树满足：
对每一个结点x，x的左子树与右子树的高度差至多为1。例如：AVL树

但是这种高度的平衡是需要付出额外的很大的代价。

那么我们退一步，采用一种“近似平衡”：
没有一条路径比其它路径长出两倍。例如：红黑树

这种近似的平衡，在不付出很大代价的情况下，可以很好的维持红黑树各项操作$O(lgn)$的时间复杂度。

4.红黑树的性质

一颗红黑树是满足下面红黑性质的二叉搜索树：

• 1.每个结点要么是红色，要么是黑色
• 2.根结点是黑色的
• 3.每个叶子结点是黑色的
• 4.如果一个结点是红色的，则它的两个子结点都是黑色的
• 5.对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

5.哨兵

为了便于处理红黑树代码中的边界条件，使用一个哨兵来代表NULL。对于一颗红黑树T，哨兵$T.null$是一个与树中普通结点有相同属性的对象。它的color属性为BLACK，而其它属性$p，left，right，key$可以设为任意值。

所有指向NULL的指针都指向哨兵$T.null$。同时为了节省空间，我们用让所有NULL指针都指向一个哨兵，即整个红黑树只有一个哨兵。

我们一般画图表示红黑树时，省略哨兵结点。

二、红黑树的运行分析

1.旋转

（1）左旋与右旋

旋转操作是一种指针结构的调整。它被用在保持红黑树的性质，会在插入删除等函数中调用。

旋转分为左旋和右旋，如下图所示：

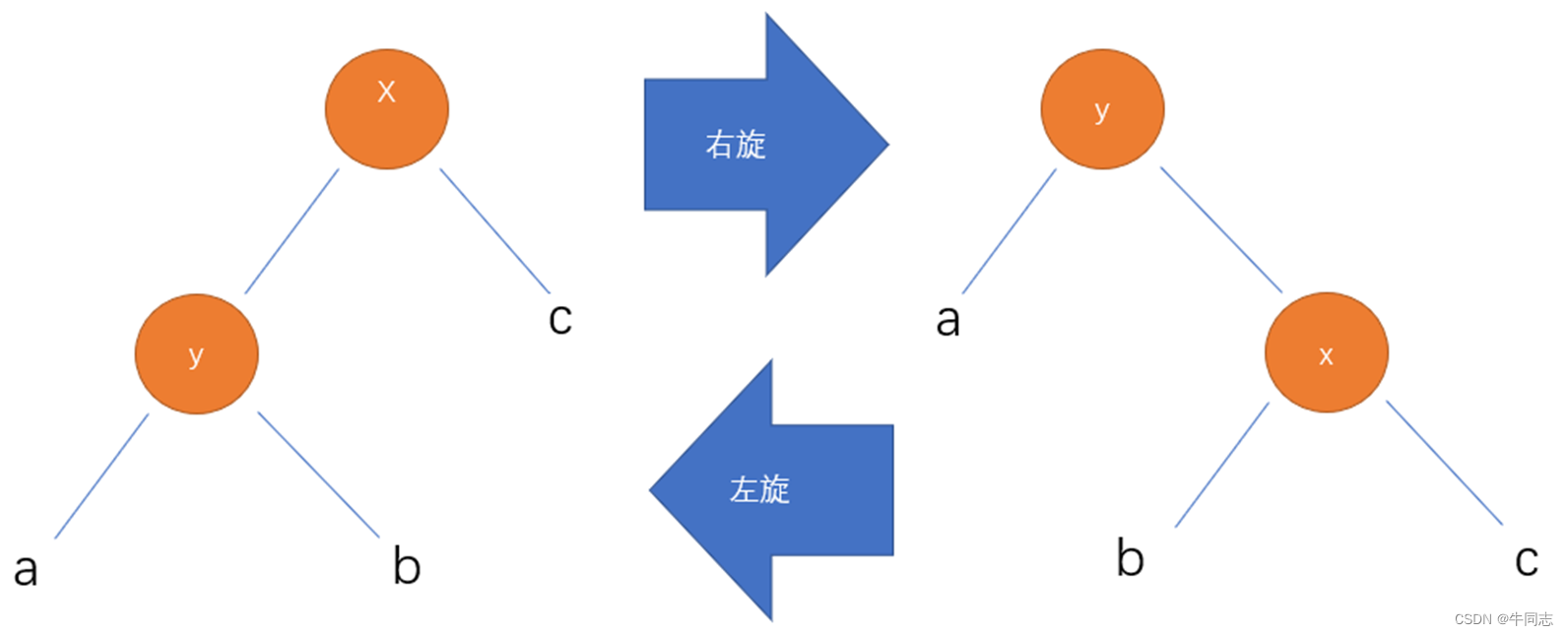
图中的a,b,c都代表着任意是子树。
注意在上面的图例中：

左旋是针对x结点，右旋是针对y结点。即是孩子结点旋转到父亲结点

（2）旋转在红黑树中的作用

旋转在红黑树中常常用来调整红黑树中的结点结构。

当我们把x,y赋予红黑两色时，旋转会有更多的物理意义，我们以上图的右旋为例：

a.x为RED，y为BLACK

根据红黑树的性质，我们可以推论c子树的根结点为BLACK，a子树的根结点可以是RED或者BLACK，b子树的根结点可以是RED或者BLACK

1.经过右旋，可能会破环红黑树的性质4

如果一个结点是红色的，则它的两个子结点都是黑色的

因为右旋后，x连接的b子树的根结点可能是RED，而x本身为RED，那么就会破坏性质4

2.一定会破环红黑树的性质5

对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

因为右旋将BLACK的y结点提至整个子树的根结点，会让左右路径都包含黑色结点y；而没有右旋前只有左边的路径包含黑色结点y

b.x为BLACK，y为BLACK

根据红黑树的性质，我们可以推论c子树的根结点为RED或者BLACK，a子树的根结点可以是RED或者BLACK，b子树的根结点可以是RED或者BLACK

1.经过右旋，不会破环红黑树的性质4

如果一个结点是红色的，则它的两个子结点都是黑色的

因为x与y都是BLACK，无论左旋右旋都不会违反性质4

2.一定会破环红黑树的性质5

对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

因为右旋将后，根结点的BLACK属性没有变，但是左边的BLACK属性结点被换到了右边，造成了黑色结点的不平衡

c.x为BLACK，y为RED

根据红黑树的性质，我们可以推论c子树的根结点为BLACK，a子树的根结点可以是BLACK，b子树的根结点可以是BLACK。

1.经过右旋，不会破环红黑树的性质4

如果一个结点是红色的，则它的两个子结点都是黑色的

2.一定会破环红黑树的性质5

对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

d.x为RED，y为RED

根据红黑树的性质，我们可以推论c子树的根结点为BLACK，a子树的根结点可以是BLACK，b子树的根结点可以是BLACK

1.经过右旋，不会破环红黑树的性质4

如果一个结点是红色的，则它的两个子结点都是黑色的

因为两个结点都是红色，位置改变没有影响

2.不会破环红黑树的性质5

对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

因为两个结点都是红色，位置改变没有影响

2.插入

（1）插入新结点

红黑树插入新结点的方法和普通的二叉搜索树是一样的。新的结点都是在满足性质的情况下，作为叶子结点插入的。
（想了解一般二叉搜索树的读者可以参考文章：）
《算法导论》学习（十五）----二叉搜索树（C语言）

不同之处有如下三个地方：

• 红黑树中，所有的空指针都指向NULL哨兵结点
• 插入的新结点按照规定，为其赋红色
• 插入后需要维护红黑树的性质

（2）插入新结点会导致的问题

a.问题一：性质2被破坏

性质2：

根结点是黑色的

如果插入的红色新结点正好是作为根结点，那么会违反性质2。

那么此时只需要将结点颜色修改为黑色即可。

b.问题二：性质4被破坏

性质4：

如果一个结点是红色的，则它的两个子结点都是黑色的

如果插入的新的红结点为z，那么z的父结点恰好也是红色的话，那它就违反了性质2。

（3）维护红黑树性质

a.情况一：

情况描述：

• 结点y为插入的新的红色结点，将其作为观测节点。
• y结点的父结点x，叔结点u，都是红色的。爷爷结点z是黑色的

那么我们有如下的解决方案：

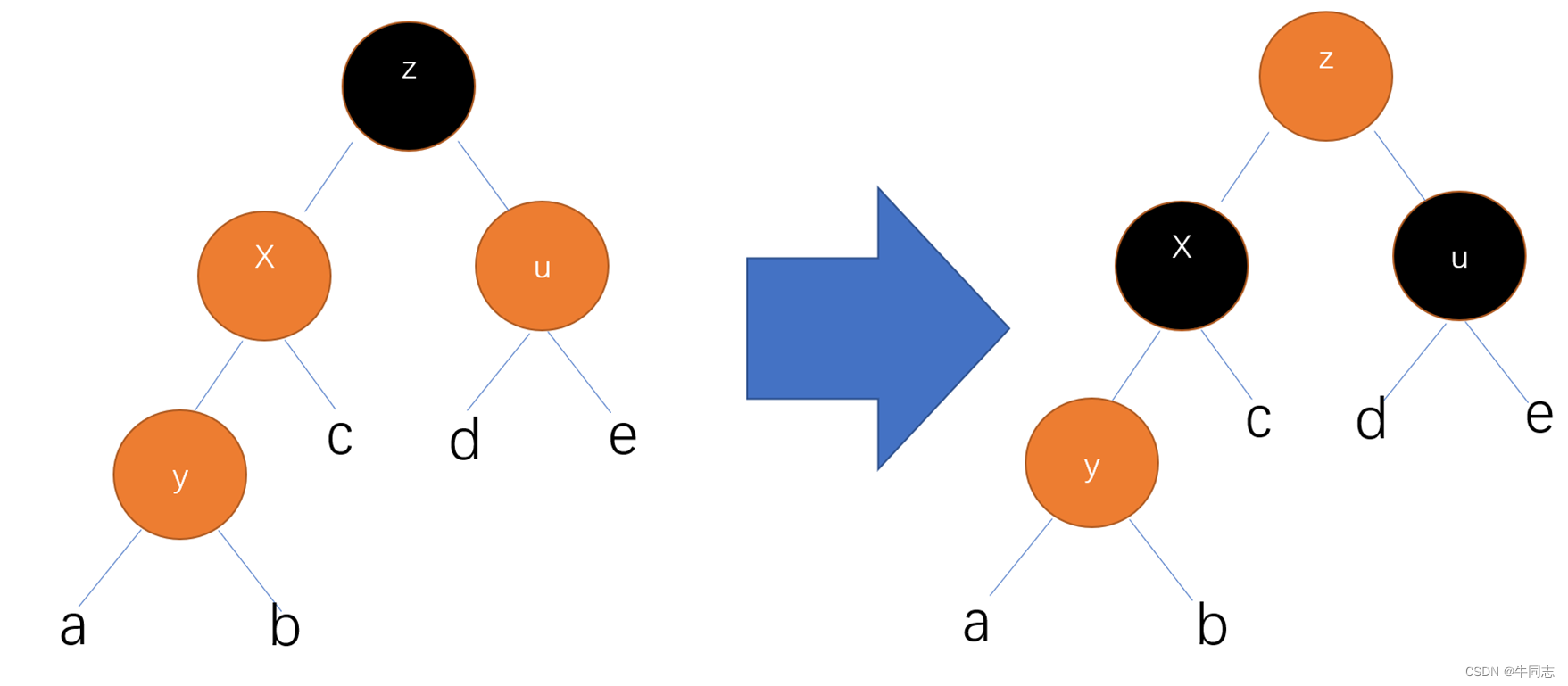
• 不改变结点的位置结构，仅仅将y结点的父结点x，叔结点u着黑色；爷结点z着红色。
• 将调整的观测结点设置为z。

这个操作的功能：

• 将情况1转化为情况2进行解决
• 保证了性质五不被破坏
  
  

b.情况二：

情况描述：

• 观测结点是红色的结点x，它的父结点y是红色的，它的叔结点d是黑色的。
• 观测结点x是父结点的右孩子

我们进行如下操作：

• 以观测结点x的父结点y为轴，进行左旋操作。

该操作的功能：

• 可以将情况2转为情况3处理
• 根据前面对旋转操作的分析，该操作不会破坏红黑树的任何性质
  

c.情况三：

情况描述：

• 观测结点是红色的结点y，它的父结点x是红色的，它的叔结点d是黑色的。
• 观测结点x是父结点的左孩子

我们进行如下操作：

• 将父结点x着黑色，爷结点z着红色
• 然后以z结点为轴，进行右旋操作

该操作的功能：

• 保证了红黑树全部性质的满足
  

3.删除

（1）删除结点

红黑树删除结点的方法和普通的二叉搜索树是一样的。删除的结点而空缺的位置会被它的后继结点填补
（想了解一般二叉搜索树的读者可以参考文章：）
《算法导论》学习（十五）----二叉搜索树（C语言）

不同之处有组要如下：

• 红黑树中，所有的空指针都指向NULL哨兵结点
• 需要在过程中跟踪填补空缺的结点的位置，以便之后的调整
• 需要记录删除结点的颜色
• 最后需要维护红黑树的性质

（2）删除结点会导致的问题

首先要明确问题是出在填补删除结点的空缺上。
比如说：
z结点被删除，y结点代替了z结点的位置，并且着与z结点同样的颜色。那么y结点原来的位置，就由y结点的右子树的根结点c来填补（因为y结点是z结点的后继，不可能有左子树）。
那么问题就来了：

• 如果y是黑色，那么y的缺失就会导致红黑树的性质被破坏
• 如果y是红色，那么不会有性质被破坏

a.问题一：

如果y是黑色，且y是原来的根结点，那么如果y的红孩子成了新的根结点，那么会违反性质2：

根结点是黑色的

b.问题二：

如果y是黑色，且y的父亲结点是红色的，那么如果y的孩子结点也是红色的话，就会违反性质4：

如果一个结点是红色的，则它的两个子结点都是黑色的

c.问题三：

如果y是黑色，那么y的缺失一定会导致包含y的路径上的黑色少1，那么就会违背性质5：

对每一个结点，从该结点到其所有后代叶结点的最短路径上，均包含相同数目的黑色结点

（3）维护红黑树的性质

关键思维：
维护的关键点在于解决性质5的破坏。为此我们需要将两边的黑结点个数保持平衡。

注意：

该部分的图片的结点颜色有一定的问题，具体颜色以文字说明为主

a.情况一：

情况描述：

• x是观测结点，也就是y的孩子结点
• x的兄弟结点y是红色的
• x的父结点z是黑色的，兄弟结点y的孩子结点是黑色的

我们进行操作：

• 将z变为红色，y变为黑色
• 以z为轴进行左旋操作
• v是x的兄弟节点

该操作的功能有：

• 不会再违反红黑树的任何性质
• 将情况1转为情况2，3，4进行处理
  

b.情况二：

情况描述：

• 观测结点是x
• x的兄弟结点y是黑色的，它的两个孩子结点也是黑色的
• x的父结点z是可以为红色也可以为黑色的

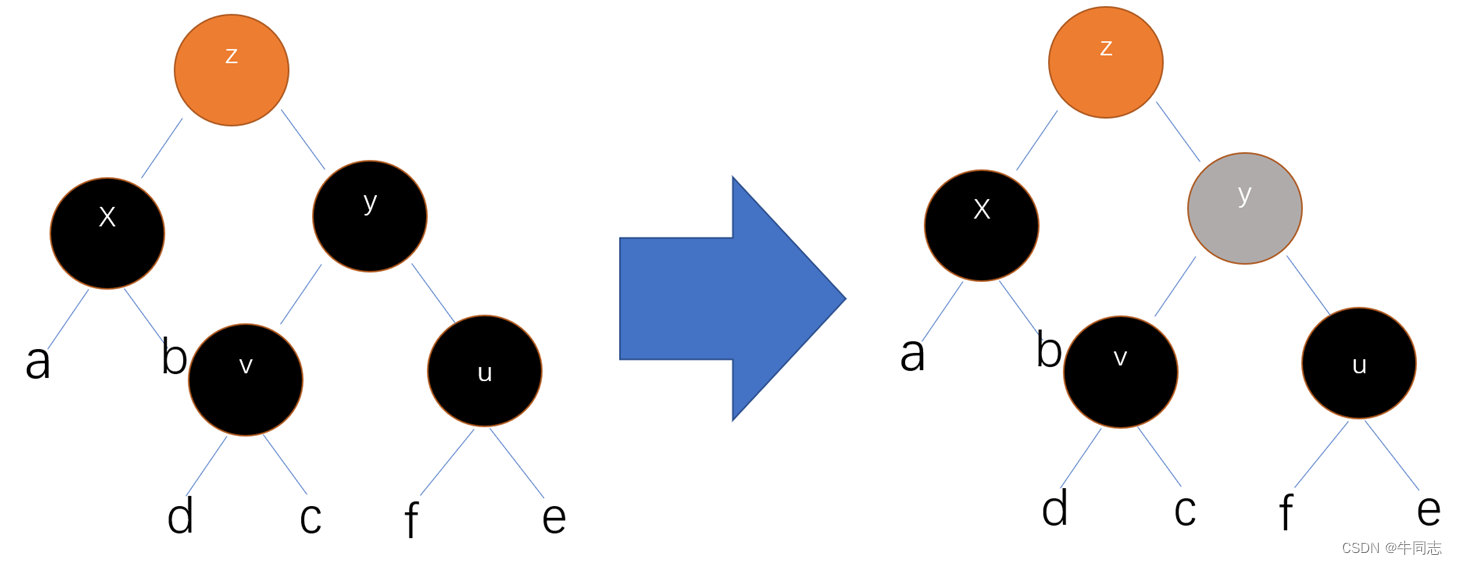
我们进行操作：

• 将x的兄弟结点y着红色
• 将z结点作为新的观测结点
• 如果z结点是红色的话，会将z结点着黑色，完成调整（从情况1变为情况2，就是这种情况）
• 如果z结点是黑色的话，说明性质5还未修复
  该操作的功能有：
• 可以解决一部分情况下的修复工作
  

c.情况三：

情况描述：

• x为观测结点
• x的兄弟结点y为黑色
• y的左孩子v为红色，有孩子u为黑色
• x是父结点可以是黑色也可以是红色

我们进行操作：

• 将v着为黑色，y着为红色
• 以y为轴进行右旋操作
• v是x的新的兄弟结点

该操作的功能有：

• 不在违反红黑树的任何性质
• 将情况3转变为情况4进行处理
  

d.情况四：

情况描述：

• x是观测结点
• y是x的兄弟结点，为黑色
• y的左孩子和x的父结点可以是黑色也可以是红色
• y的右孩子是红色的

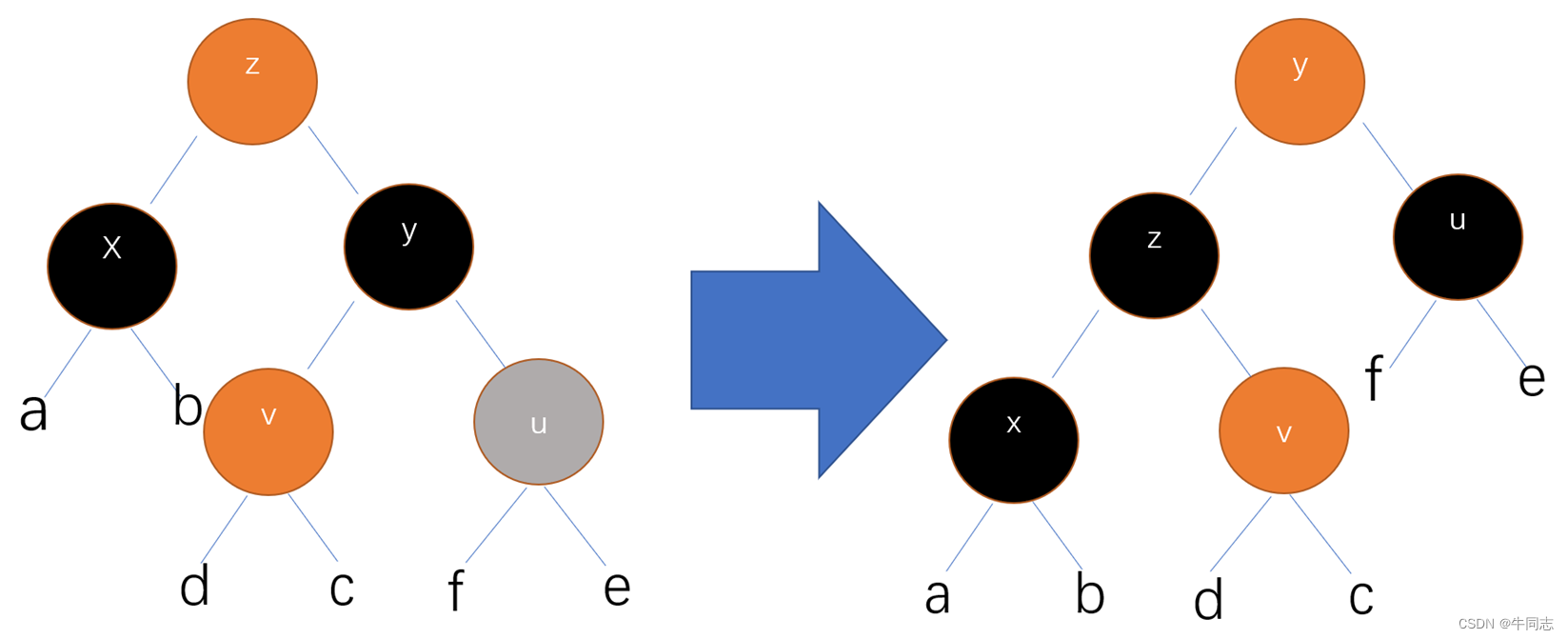
我们进行操作：

• 将z着为黑色，y着为红色，u着为黑色
• 以z为轴进行左旋操作

该操作的功能有：

• 解决了情况2剩余的性质五遭破坏的问题
• 完成整个维护过程
  

三、红黑树的时间复杂度分析

红黑树的调整过程所消耗的循环都是常数级的，因此不会在调整上花过多的时间。
同时又因为其是“近似平衡”的二叉搜索树。
综上：红黑树的所有操作都稳定在$O(lgn)$

---

总结

文章不妥之处请各位读者包涵和指正。
二叉搜索树的相关内容可以参考文章：
《算法导论》学习（十五）----二叉搜索树（C语言）