python数据结构补充——树

定义

• 非线形结构：每个元素都可以有多个前驱或者后继
• 树是n(n>=0)个元素的集合：n=0时，称为空树；树只有一个特殊的没有前驱的元素，称为树的根（Root）；树中除了根节点之外，其他元素只有一个前驱，可以有0个或者多个后继
• 树是非线性结构

树的递归定义

• 树T是n(n>=0)个元素的集合：n=0时，称为空树
• 有且只有一个特殊元素根，剩余元素都可以被划分为m个互不相容的集合T1 、T2、T3 ……Tm，而每一个集合都是树，称为T的子树（Subtree）
• 子树也有自己的根

树中各个名称的概念

• 结点：树中的数据元素（下图中的A、B、C……等元素）
• 结点的度：结点拥有的子树的数目为度，记作d(v)（下图中，对于A来说有两个子树，他的度就是2；对于B来说，只有一个子树，因此度是1）
• 叶子结点：结点的度为0，称为叶子结点leaf，终端结点，末端结点（下图中G、H、I、J、F都是叶子结点）
• 分支结点：结点的度不为0，称为非终端结点或者分支结点（除叶子结点之外的，都是分支结点）
• 分支：结点之间的关系（两个结点的连写就是分支，也叫关系，因此A、B之间的链接叫做分支）
• 内部结点：除根节点之外的分支结点，当然也不包括叶子结点（下图中，B、C、D、E都是内部结点）
• 树的度是树内个结点的度的最大值。下图中D结点度最大为3，树的度树就是3
  
• 孩子(儿子Child)结点：结点的子树的根节点成为该结点的孩子（B、C为A结点的孩子结点）
• 双亲(父Parent)结点：一个结点是它各子树的根节点的双亲（A 是B的父结点，B是D的父结点）
• 兄弟(Sibling)结点：具有相同双亲结点的结点（B和C为兄弟结点；G、H、I也是兄弟结点）
• 祖先结点：从根节点到该结点所以经分支上的所有结点（A、B、D为G、H、I的祖先结点）
• 子孙结点：结点的所有子树上的结点都称为该结点的子孙（A下面所有的结点（B、C……J都是A的子孙结点）
• 结点的层次（Level）：根节点是第一层，根的孩子是第二层，以此类推，记作L(v)（上图的树有4层）
• 树的深度（高度Depth）:树的层次的最大值（上图中，树的深度是4）
• 堂兄弟：双亲在同一层的结点（D和E、D和F就是堂兄弟）
• 有序树：结点的子树是有顺序的（兄弟有大小，有先后顺序），不能交换，（也就是说B子树和C子树不能交换）
• 无序树：结点的子树是无序的，可以交换，但一般情况下遇到问题往往都是有序树
• 路径：树中的k个结点：n1、n2、……nk,满足ni是n(i+1)的双亲，成为n1到nk的一条路径。就是一条线串下来。前一个都是后一个的父结点（例如：A、B、D、G就是一条路径）
• 路径长度：路径上的结点数-1，也就是分支数（A、B、D、G的长度为3）
• 森林：m(m>=0)棵不相交的树的集合。对于结点而言，其子树的集合就是森林。A结点的2棵子树（B和C）的集合就是森林

特点

• 除了空树之外，都有唯一的根
• 没有父节点的节点，为根节点，每一个根节点有且只有一个父节点
• 子树不可相交
• 除了根结点之外，每个元素只能有一个驱动，可以有零个或者多个后继
• 根结点没有双亲结点（前驱），叶子结点没有孩子结点（后继）
• vi是vj的双亲，则L(vi)=L(vj)-1（vi比vj的层次少1）,也就是说双亲比孩子结点的层次小1
• 堂兄弟的双亲不一定是兄弟。上图中I和J是堂兄弟，但是他们的父母D和E并不是兄弟

存储和使用场景

• 树的存储有两种形式：
• • 顺序存书：将数据结构存储在固定的数据中，在遍历上有一定的优势
• • 但是因为所占据的空间太大，是非主流的二叉树
• • 链式存储：二叉树常用的存储方式
• • 每个节点可以指向多个后继的数据，缺陷：指针域中的指针个数不定
• • 解决方案：将多叉树，转换为二叉树
• 顺序存储方式的示例图如下：
• 树的应用场景：
• • xml、html等，怎么让编写这些东西的解析器的时候，不可避免的需要使用
• • 路由协议就是使用了树的算法
• • mysql的数据库索引
• • 文件系统的目录结构

二叉树

• 每个结点最多2棵子树，二叉树不存在度树大于2的结点
• 他是有序树，左子树和右子树是顺序的，不可交换次序
• 即使某个结点只有一棵子树，也要确定它是左子树还是右子树

二叉树的基本形态

• 空二叉树（空树）
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点有左子树和右子树

斜树

• 左斜树：所有结点都只有左子树
• 右斜树：所有结点都只有右子树

满二叉树

• 一个二叉树的所有分支结点都存在于左子树或者右子树，且所有叶子结点只存在于最下面一层
• 同样深度的二叉树中，满二叉树的结点最多
• k为深度(1
• 下图就是一个深度为4的15结点的满二叉树
  

完全二叉树

• 若二叉树的深度为k，二叉树的层数从1到k-1层的结点数都达到了最大个数，在第k层的所有结点都集中在最左边，这就是完全二叉树
• 完全二叉树由满二叉树引出
• 满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树
• k为深度(1

【备注】上图符合完全二叉树

【备注】上图也符合完全二叉树，因为4的左边已经存在子树

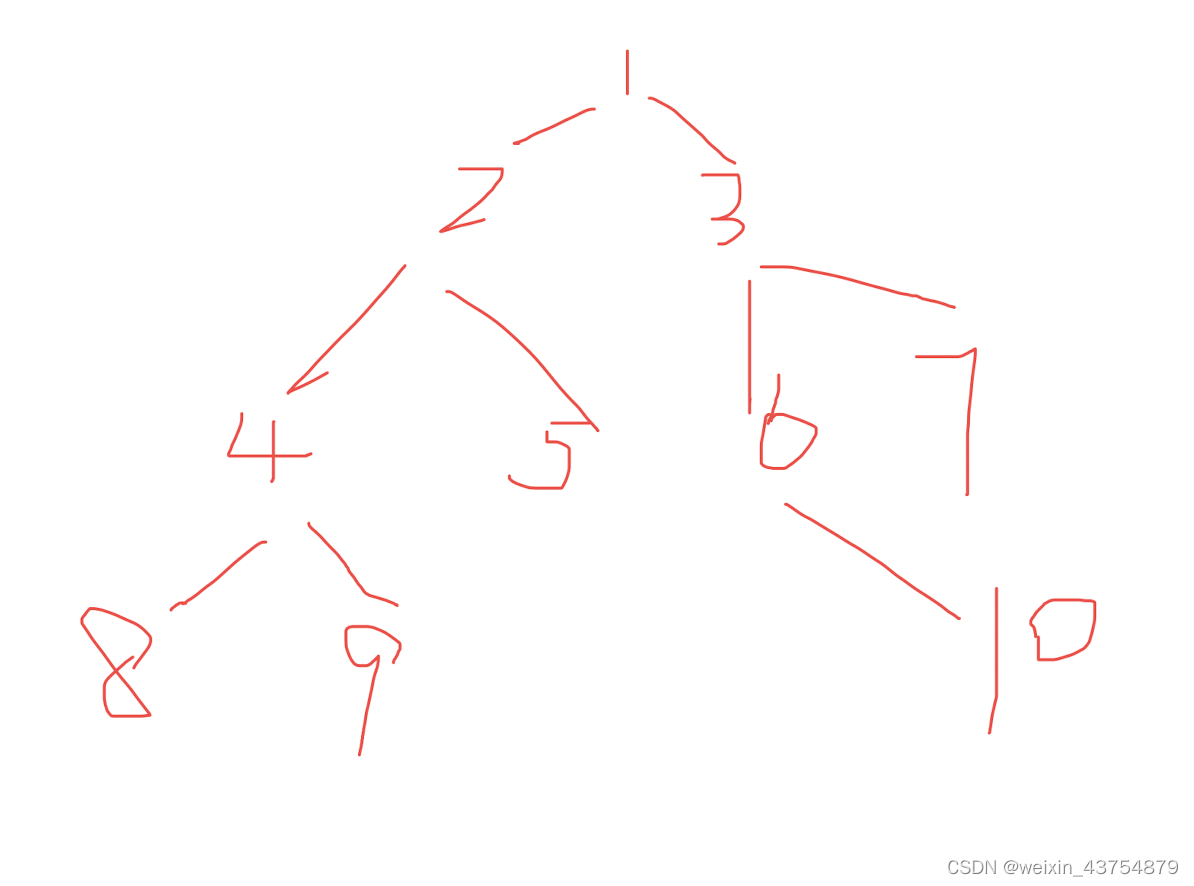
【备注】上图就不是完全二叉树，因为6没有左子树；4和5下面没有子树

【备注】上图就不是完全二叉树，因为4下面没有子树，最后一层子树的顺序应该是4-5-6-7，不能直接在9下面添加子树

二叉树的性质

• 性质1:在二叉树的第i层上至多有 2的(i-1)次方个结点(i>=1)
• 性质2:深度为k的二叉树，至多有（2的k次方）-1个结点(k>=1)
• 一层：2-1=1
• 二层：4-1 = 1+2 = 3
• 三层：8-1 = 1+2+4 = 7
• 性质3：对任何一颗二叉树T，如果其终端结点数为n0，度数为2的结点为n2，则n0=n2+1；换句话说：叶子结点树数-1就等于度数为2的结点数
• 如下图：叶子结点是8，5，6，7，一共四个，度数二2的结点是：1，2，3，一共三个，正好是叶子结点树数-1
  【备注】度数为2指的是，结点下面有两个分支
  
• 其他性质：高度为k的二叉树，至少有k个结点
• 含有n(n>=1)的结点的二叉树高度多为n，最小为math.cell(log2(n+1))，不小于对数值的最小整数，向上取整

【解析】高度为k的二叉树，如果只有一个路径（斜树），就是有k的结点，高度也只多为k；math.cell(log2(n+1))指的是取（n+1）的对数，然后向上取整
例如：如果结点是8，那么计算公式就为log2(8+1)，因为log2(8)=3，所以log2(8+1)肯定大于3，向上取整就是4层

• 性质4具有n个结点的完全二叉树的深度为int(log2n)+1或者math.cell(log2(n+1))
  【备注】int(log2n)指的是取n的对数，然后取整型，小数取整型时时直接去掉小数

• 性质5 有n个结点的完全二叉树（深度为性质4），结点按照层序编号（如下图），各个节点之间的关系如下：
  
  1.如果i=1，则i结点是根结点，无双亲，
  2.i>1，则其双亲时int(i/2)，向下取整。就是子结点的编号整除2得到的度结点的编号。福结点如果时i，那么左侧的编号就是2i，右侧的编号就是2i+1
  3.如果2i>n，则结点i无左侧树，即结点i为叶子结点，否则其左侧子结点的编号就是2i
  4.如果2i+1>n，则结点i没有右结点，注意这里并不能说明i没有左结点，否则有结点的编号就是2i_1

树的遍历/二叉树的遍历顺序

• 遍历：迭代所有的元素一遍
• 树的遍历：对树中所有元素不重复的访问一遍，也可以称作扫描
• 树遍历的方式有以下几种：
• 广度优先遍历：他也叫宽度优先遍历，一次奖一层的元素拿完之后，才能去拿下面的元素，也叫层序遍历
• 深度优先遍历：一次将一支子树中的元素全部拿完之后，再去获取别的子树中的元素。深度优先有三种遍历方式，即：前序遍历，中序遍历，后序遍历
• 遍历序列：将树中所有的元素遍历一遍，得到的元素的序列，将层次结构换成了线性结构

层序遍历

• 按照树的层次，从第一层开始，自左向右遍历元素
• 遍历序列：以下图为例，顺序为A->B->C->D->E->F->G->H->I
• 遍历二叉树的元素时，需要有一个数据结构将二叉树中的结点和节点之间的关系描述出来，然后才能去遍历，因此这种数据结构一般是顺序的，常用列表来表示
  

树的构建，添加及层序遍历的代码

class Node():
    ''' 树的节点'''

    def __init__(self,item):
        self.item = item # 树节点上的数据
        '''树和链表不一样的地方在于：
        树有两个后继节点，链表只有一个'''
        self.l_next = None # 树的左节点指向
        self.r_next = None # 树的右节点指向

class  Tree_data():
    ''' 构造二叉树'''

    def __init__(self):
        ''' 空二叉树的构建'''
        self.root = None

    def add(self,item):
        '''二叉树添加数据，尾部追加'''
        ''' 广度优先的方式追加遍历元素'''
        node = Node(item)# 构造二叉树的节点
        if self.root is None:
            self.root = node
            return
        queue = [self.root] # 二叉树的队列，里面的元素为根节点
        # 需要循环,追要队列不为空，就需要从中弹出元素确认
        while queue:
            # 判断节点的左子树或者右子树是否为空，如果不为空，将其追加到队列中
            cur_node = queue.pop(0)# 当前拿到的节点
            if cur_node.l_next is None:
                cur_node.l_next = node
                return
            else:
                queue.append(cur_node.l_next)

            if cur_node.r_next is None:
                cur_node.r_next = node
                return
            else:
                queue.append(cur_node.r_next)

    def breadth_travel(self):
        '''广度优先遍历'''

        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            print(cur_node.item)
            if cur_node.l_next is not None:
                queue.append(cur_node.l_next)
            if cur_node.r_next is not None:
                queue.append(cur_node.r_next)
if __name__ == '__main__':
    t = Tree_data()
    t.add(10)
    t.add(1100)
    t.add(1000)
    t.add(80)
    t.add(88)
    t.breadth_travel()
*************************run_result***************
10
1100
1000
80
88

深度优先遍历

• 设定树的根结点为D，左子树为L，右子树为R，且要求L一定在R前面，则有以下几种遍历方式
• 前序遍历：也叫先序遍历，也叫先根遍历，DLR
• 中序遍历，也叫中根遍历，LDR
• 后序遍历，也叫后根遍历，LRD

前序遍历

• 从根结点开始，先左子树，后右子树
• 每个子树内部依然是先根结点，再左子树，然后右子树
• 下图的遍历顺序是：A->B->D->G->H->C->E->I->F
• 先遍历根结点，因此第一个元素是A，然后先左子树B，下面还有左子树，因此顺序是D、G；后面没有左子树了，找右子树，因此后面是H；因为D和B都没有右子树，因此下一个右子树就是C，再找左子树E、I，接下来找右子树：F
  

中序遍历

• 从根结点的左子树开始遍历，然后是根结点，再右子树
• 每个子树内部，也是先左子树，然后根节点，再右子树，递归遍历
• 遍历序列，有两种，分别是：G->D->H->B->A->I->E->C->F
• 先遍历最底部的左子树结点，也就是G，然后遍历这个结点的根结点D，然后又结点H，在到上一级的根结点B、A；然后是右子树最下面结点的左子树I、E，然后是是他的根结点C，右子树F
  
• 下图，因为I是E的右子树（E没有左子树，直接去根结点），因此遍历顺序为：G->D->H->B->A->E->I->C->F
  

后序遍历

• 先左子树，后右子树，最后根结点
• 每个子树内部依然是先左子树，后右子树，最后根结点，递归遍历
• 遍历序列是：G->H->D->B->I->E->F->C->A
  

class Node():
    ''' 树的节点'''

    def __init__(self,item):
        self.item = item # 树节点上的数据
        '''树和链表不一样的地方在于：
        树有两个后继节点，链表只有一个'''
        self.l_next = None # 树的左节点指向
        self.r_next = None # 树的右节点指向

class  Tree_data():
    ''' 构造二叉树'''

    def __init__(self):
        ''' 空二叉树的构建'''
        self.root = None

    def add(self,item):
        '''二叉树添加数据，尾部追加'''
        ''' 广度优先的方式追加遍历元素'''
        node = Node(item)# 构造二叉树的节点
        if self.root is None:
            self.root = node
            return
        queue = [self.root] # 二叉树的队列，里面的元素为根节点
        # 需要循环,追要队列不为空，就需要从中弹出元素确认
        while queue:
            # 判断节点的左子树或者右子树是否为空，如果不为空，将其追加到队列中
            cur_node = queue.pop(0)# 当前拿到的节点
            if cur_node.l_next is None:
                cur_node.l_next = node
                return
            else:
                queue.append(cur_node.l_next)

            if cur_node.r_next is None:
                cur_node.r_next = node
                return
            else:
                queue.append(cur_node.r_next)

    def preorder(self,node):
        '''
        前序遍历 /先序遍历
        :param root: 每次遍历子树的根节点
        :return:
        '''
        # 退出递归的条件
        if node == None:
            return
        print(node.item,end=" ") # 打印当前子树的根节点
        self.preorder(node.l_next)# 递归根节点的左子树
        self.preorder(node.r_next)  # 递归根节点的右子树

    def inorder(self,node):
        '''
        中序遍历
        :param root: 每次遍历子树的根节点
        :return:
        '''
        # 退出递归的条件
        if node == None:
            return
        self.inorder(node.l_next)  # 递归根节点的左子树
        print(node.item,end=" ") # 打印当前子树的根节点
        self.inorder(node.r_next)  # 递归根节点的右子树

    def aftorder(self, node):
        '''
        后序遍历
        :param root: 每次遍历子树的根节点
        :return:
        '''
        # 退出递归的条件
        if node == None:
            return
        self.aftorder(node.l_next)  # 递归根节点的左子树
        self.aftorder(node.r_next)  # 递归根节点的右子树
        print(node.item, end=" ")  # 打印当前子树的根节点

if __name__ == '__main__':
    t = Tree_data()
    t.add(0)
    t.add(1)
    t.add(2)
    t.add(3)
    t.add(4)
    t.add(5)
    t.add(6)
    t.add(7)
    t.add(8)
    t.add(9)
    t.preorder(t.root)
    print(" ")
    t.inorder(t.root)
    print(" ")
    t.aftorder(t.root)
*******************run_result***************
0 1 3 7 8 4 9 2 5 6  
7 3 8 1 9 4 0 5 2 6  
7 8 3 9 4 1 5 6 2 0

二叉树之由遍历确认一棵树

• 必须给出中序的顺序序列
• 然后由中序和先序，可推断后序
• 也可以由后序和中序，腿短先序
• 方式：由先序/后序确认根节点，先序在最前面，后序在最后面
• • 然后根据根节点，将中序分为两部分，取两部分的最后一个，为二级根节点
• • 然后在将大于3个元素的子序列，根据二级根节点再分为两部分，取最后一个满3个元素的数值，为三级根节点
• • 然后中序和先序/后序配合，确认树的形状

堆 Heap

• 堆是一个完全二叉树
• 每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆（非叶子结点一定有孩子，要求其一定大于或者等于他的左右孩子，根结点等于左右结点中比较大的，就是大顶堆）
• 每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆非叶子结点一定有孩子，要求其一定小于或者等于他的左右孩子，根结点等于左右结点中比较小的，就是小顶堆）
• 根结点有一定是大顶堆中的最大值，一定是小顶堆中的最小值

大顶堆

• 完全二叉树的每个非叶子结点都要大于或者等于其左右孩子结点的值
• 根结点一定是大顶堆中的最大值
• 如下图
  

小顶堆

• 完全二叉树的每个非叶子结点都要小于或者等于其左右孩子结点的值
• 根结点一定是小顶堆中的最小值