-
2-反对称矩阵及其指数函数
1.反对称矩阵
(1)定义: A为n阶矩阵,如果A的转置等于-A,则称A为“反对称矩阵”.即A'=-A
(2)特征: A主对角线两边对称的数相反,且主对角线的数全为0
(3)性质:
a.设A,B为反对称矩阵,则A±B仍为反对称矩阵
b.设A,B为反对称矩阵, 则A'或bA仍为反对称矩阵
c.设A为反对称矩阵,B为对称矩阵,则AB-BA为对称矩阵
d.幂运算
其中,(V X)为反对称矩阵, v为(V x)的模值.

(4)定理:
a.奇数阶反对称矩阵的行列式必为0
b.反对称矩阵的特征值是0或纯虚数,并且对应于纯虚数的特征向量的实部和虚部形成的实向量等长且互相正交2.反对称阵的矩阵指数函数
(1)实数x的指数函数的展开式

(2)同理,(对称)矩阵A的 指数函数的展开式
知识补充:
1.行列式运算
(1)二阶行列式运算
主对角线的数乘 减去 副对角线的数乘:a11a22 - a12a21
(2)三阶行列式运算

2. 矩阵叉乘和点乘(内积)(1)矩阵叉乘运算
矩阵w=NxM阶,x=nxN阶,w的行数必须等于x的列数
(2)矩阵的点乘
两矩阵阶数相同,点乘为两矩阵个元素相乘

3.向量的叉乘和点乘
(1)向量的叉乘
向量叉乘的运算结果是一个向量,叉乘所得的新“向量"与这两个向量垂直.新向量的模等于:
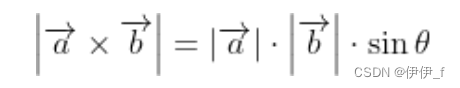
新向量的方向:
与这两个向量所在的平面垂直,且遵循右手定则
(2)向量的点乘
向量的点乘结果是一个标量(数值)
4. 对称矩阵
(1)定义: A为n阶矩阵,如果A的转置等于A,则称A为“对称矩阵”.即A'=A
(2)特征: A主对角线两边对称的数相等5.对角矩阵
(1)对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵。
a.对角线上的元素可以为0或其他值.
b.对角线上元素相等的对角矩阵称为数量矩阵

c.对角线上元素全为1的对角矩阵称为单位矩阵
(2)对角矩阵运算
a.和差运算
b.数乘运算
c.点乘运算
6.实对称矩阵
(1)定义: 如果n阶矩阵A的元素都是实数且其转置等于本身A'=A,则称A为实对称矩阵
(2)性质:
a.实对称矩阵A的不同特征值对应的特征向量是正交的。
b.实对称矩阵A的特征值都是实数。
c.n阶实对称矩阵A必可相似对角化,且相似对角阵上的元素即为矩阵本身特征值。
d.若A具有k重特征值λ0 必有k个线性无关的特征向量,或者说秩r(λ0E-A)必为n-k,其中E为单位矩阵。
e.实对称矩阵A一定可用正交矩阵对角化7.厄米特矩阵
(1)定义:指的是自共轭矩阵
矩阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等.埃尔米特矩阵主对角线上的元素都是实数的
例如A为厄米特矩阵
8.反厄米特矩阵

9.正交矩阵
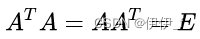
10.酉矩阵

若A是n阶厄米特矩阵,其特征值对角阵为V,则存在一个酉矩阵U,使AU=UV。
11.正规矩阵


12.特征值和特征向量

13.哈密-凯莱(Hamilton-Cayley)定理
(1)定理
定理1(Hamilton-Cayley定理)设A是数域F上的n阶矩阵,f(λ)=|λE-A|是A的特征多项式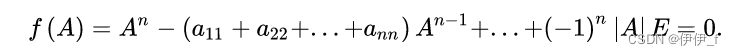
-
相关阅读:
亚马逊国际按关键字搜索商品 API 返回值说明
太全了——用Python操作MySQL的使用教程集锦
【rar密码】WinRAR整理密码,如何使用?
VUE3+vite项目中动态引入组件和异步组件
Spring事务传播机制
从0到1学SpringCloud——10 springboot集成redis缓存
信息系统项目管理师核心考点(五十四)配置项分类、状态与版本
java-php-python-ssm-快递代收系统-计算机毕业设计
电极的制作方法详解
STM32实战总结:HAL之wifi
- 原文地址:https://blog.csdn.net/fanxianchao_2012/article/details/126972574