第三章---堆栈队列 板子

封装栈操作

class Stacks {
public:
	int getTopNum() {//未进行判空，所以使用之前先判空
		return Stack[top];
	}

	bool isEmpty() {
		return top == -1 ? true : false;
	}

	bool pop() {
		if (isEmpty()) {
			return false;//空栈无法弹栈
		}
		top--;
		return true;
	}

	void push(int i) {
		Stack[++top] = i;
	}
private:
	//完整栈操作
	long long Stack[10005];//考试时直接根据题目开足够大的空间
	int top = -1;
};

1、求逆波兰数板子

详细描述见：力扣150. 逆波兰表达式求值

2、括号匹配

1、板子：力扣 20. 有效的括号(这道题是括号问题的大模型)

2、前缀转后缀

处理三个问题
1、操作符(±*/)：入栈
2、右括号：写入结果集+弹一次栈放进结果集
3、其余所有符号：直接写入结果集

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
void function_four() {
	char ans[100];//结果集
	int ans_n = 0;

	string item;
	cin >> item;
	int n = item.size();

	char stacks[100];//栈
	int point = 0;//栈顶指针

	for (int i = 0; i < n; i++) {
		if (item[i] == '+' || item[i] == '-' || item[i] == '*' || item[i] == '/') {
			stacks[point++] = item[i];
		}
		else if (item[i] == ')') {
			ans[ans_n++] = ')';
			ans[ans_n++] = stacks[--point];
		}
		else {
			ans[ans_n++] = item[i];
		}
	}

	for (int i = 0; i < n; i++) {
		cout << ans[i];
	}
}
int main()
{
	function_four();
	return 0;
}

3、中缀转后缀(对"计算公式"进行转化)

1、对相应符号"(#±*/"等先进行优先级的定义

	int priority[200] = {};
	priority['#'] = -1, priority['('] = 0;
	priority['+'] = 1, priority['-'] = 1;
	priority['*'] = 2, priority['/'] = 2;

2、对于非操作符，直接输出
3、遇到操作符：
<1>左括号：直接入栈
<2>右括号：弹栈，直到遇到左括号为止(这里的边界是把左括号也弹出去，所以读取完栈之后马上弹出)
<3>操作符(非左右括号)优先级高于栈顶：直接入栈
<4>操作符(非左右括号)优先级小于等于栈顶：弹栈，直到大于栈顶，再入栈(这里的边界是大于栈顶之后，停止弹栈，所以先读取判断，之后再弹栈)
4、结束，按照要求返回结果

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
void function_two() {
	string s = "";
	cin >> s;
	int n = s.size();

	int priority[200] = {};
	priority['#'] = -1, priority['('] = 0;
	priority['+'] = 1, priority['-'] = 1;
	priority['*'] = 2, priority['/'] = 2;

	stack<char> help;
	help.push('#');
	for (int i = 0; i < n; i++) {//整个过程就是模拟
		if (s[i] >= '0'&&s[i] <= '9') {//遇到数字直接输出
			cout << s[i];//具体怎么处理看题目
		}
		else {//操作符
			if (s[i] == '(') {//遇到左括号直接压栈
				help.push(s[i]);
			}
			else if (s[i] == ')') {//遇到右括号弹栈直到遇到左括号为止
				while (1) {
					char tmp = help.top();
					help.pop();
					if (tmp == '(') {
						break;
					}
					cout << tmp;
				}
			}
			else{//遇到非括号
				char tmp = help.top();
				if (priority[s[i]] > priority[tmp]) {//当前操作符优先级更高，直接压
					help.push(s[i]);
				}
				else {//否则(要加入操作符的优先级小于等于栈顶)弹栈
					while (1) {
						char tmp = help.top();
						if (priority[s[i]] > priority[tmp]) {//直到栈顶优先级小于要加入的操作符
							break;
						}
						help.pop();//后弹栈，防止弹多了
						cout << tmp;
					}
					help.push(s[i]);//把目标压进来
				}
			}
		}
	}
	return;
}

4、前缀和问题

功能

利用前缀和，可以快速获取，一个数组，任意连续的子区间的元素和：

比如：(preSum[]数组是存储前缀和)
获取(l,r)内元素和：preSum[r]-preSum[l-1]

应用

最大子数组和问题

力扣:53. 最大子数组和
1、使用前缀和，因为我这个题就是想获得，大数组上某一段连续的区间，并且区间和最大，那么前缀和就是最快的，O(1)的复杂度就可以知道任意连续子区间的区间和(l到r之间=preSum[r]-preSum[l-1])
2、思路：核心是“控制变量，有序枚举”

1、由于子区间定义问题，一定是从左到右连续的，所以采取控制变量法枚举，不容易混乱
2、从头到尾枚举小区间终点，对于终点是i的小区间，它前面的所有子区间中，为了让子区间和最大，找前缀和最小的位置处(preSum[r]-preSum[l-1]后者越小，整体越大)，所以还需要动态维护一个最小前缀和的值
3、关于前缀和最小值的问题，当第i处完毕i++,相当于把第i处扩充进来，进来一个新元素，就需要看看原本的最小值会不会改变，这样动态维护一个前缀和最小值即可。
4、这样以i处作为结尾的所有子区间和最大值找到了，枚举所有i，在最后把这些所有的最大值中找一个最大的(动态维护ans)

class Solution {
public:
	int maxSubArray(vector<int>& nums) {
		int n = nums.size();
		vector<int> preSum(n + 1, 0);
		preSum[0] = nums[0];
		for (int i = 1; i < n; i++) {
			preSum[i] = preSum[i - 1] + nums[i];//前缀和
		}
		int ans = preSum[0];//如果只有一个元素，那么它本身就是答案
		int minSum = 0;//记录一下最小的前缀和，初始值一定要满足只有一个值，preSum[0]是答案，所以初始值为0(最小前缀和一定<=0)
		for (int i = 0; i < n; i++) {
			ans = max(ans, preSum[i] - minSum);//站在当前位置(子区间终点)，
			minSum = min(minSum, preSum[i]);//为下一个区间找到动态维护一个最小值，看看新进来的元素是不是比原来的还小
		}
		return ans;
	}
};

5、压缩存储对应关系问题

1、把二维数组，按照题意，进行压缩存储，本质上，要找好，二维和一维的对应关系即可
2、思路：计算A(i,j)前面的元素个数，对应到一维数组中的位置
3、注意事项

1、注意主对角线算不算
2、注意i和j是从0开始还是1开始，有很大的不同
3、注意是行优先还是列优先

例子(22计专P81)

本题从0开始，A(i,j)前面有i行j列；列优先(一列一列填充)；上三角且不包含对角线

结果：

6、调和级数

思路：

1、就是模拟，模拟两个分数相加，先通分相加，再分子分母一起约分到最简，这是一次的过程，不断执行上述过程，直到加完
2、初始时候，1/1

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int GCD(int a, int b) {//获得最大公约数
	return b == 0 ? a : GCD(b, a%b);
}
void function_three() {//就是若干个分数相加，为了防止分子分母干越界，所以一边加一边约分，约分就用GCD即可
	int n = 0;
	cin >> n;
	int up = 1;//分子
	int down = 1;//分母
	cout << 1 << "/" << 1 << " + ";
	for (int i = 2; i <= n; i++) {
		if (i != n) {
			cout << 1 << "/" << i << " + ";
		}
		else {
			cout << 1 << "/" << i << " = ";
		}
		up = up * i + down;//通分过程，这个自己随便写一下就知道了
		down *= i;
		int gcd = GCD(up, down);//防止越界，所以一边算一边化简
		up /= gcd;
		down /= gcd;
		if (i == n) {
			cout << up << "/" << down;
		}
	}
	return;
}

7、二维矩阵(已经排好序)快速查找目标元素

1、题目：力扣：74. 搜索二维矩阵

2、思路：利用好二维矩阵的性质，o(m+n)内完成寻找(m为行数,n为列数)

1、从 左下角(或者右上角，这个道理一样，这里不赘述)开始
2、比目标元素大，往上走，i–
3、比目标元素大，往右走，j++
4、边界判定：i>=0,j

3、代码

class Solution {
public:
	bool searchMatrix(vector<vector<int>>& matrix, int target) {
		//因为二维矩阵已经排好序，所以直接利用二维矩阵特点搜索就行
		int m = matrix.size();
		int n = matrix[0].size();
		int i = m - 1, j = 0;//从左上或者右下两个点出发搜索就行，复杂度是O(m+n)
		while (i >= 0 && j < n) {
			if (matrix[i][j] == target) {
				return true;
			}
			else if (matrix[i][j] < target) {//小于目标往右走
				j++;
			}
			else {//大于目标往上走
				i--;
			}
		}
		return false;
	}
};

8、链表问题

链表就是一个单子树的树结构，每个节点就只有一个孩子节点，所以说，所以说又时候，二叉树的一些想法，改一改，就能放到链表里面

1、链表结构

 struct ListNode {
     int val;
     ListNode *next;
     ListNode() : val(0), next(nullptr) {}
     ListNode(int x) : val(x), next(nullptr) {}
     ListNode(int x, ListNode *next) : val(x), next(next) {}
 };

2、从后向前打印链表

因为链表只能从前往后走，但是我想要从后往前打印，递归思想，类似于二叉树的后根遍历

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
 struct ListNode {
     int val;
     ListNode *next;
     ListNode() : val(0), next(nullptr) {}
     ListNode(int x) : val(x), next(nullptr) {}
     ListNode(int x, ListNode *next) : val(x), next(next) {}
 };
 void printList(ListNode* head) {//补充：逆序打印链表
	 if (head == nullptr) {
		 return;
	 }
	 printList(head->next);
	 cout << head->val;
	 return;
 }

3、反转链表(头插法)

1、重新开一个head哨兵，用于头插法
2、正向访问已知链表，头插法进入head新表
3、因为头插法，是从右向左生长，所以得到的就是反过来的链表

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
 struct ListNode {
     int val;
     ListNode *next;
     ListNode() : val(0), next(nullptr) {}
     ListNode(int x) : val(x), next(nullptr) {}
     ListNode(int x, ListNode *next) : val(x), next(next) {}
 };
 	 ListNode* Reverse(ListNode* l) {
		 ListNode* head = new ListNode();//新表用于头插法的哨兵节点
		 ListNode* p = l;
		 while (p != nullptr) {
			 ListNode* tmp = p;
			 p = p->next;
			 tmp->next = head->next;
			 head->next = tmp;
		 }
		 return head->next;
	 }

4、判断回文链表

1、例题：力扣：234. 回文链表
2、思路：直接针对链表操作，空间复杂度O(1),时间O(n),考试实在不会了，就转化成数组做，绝对不可以空着

1、回文链表就是以链表中间为中心点两边对称，所以第一步，快慢指针定位中心
2、因为经观察发现，元素个数为奇数，slow恰好指向单个的回文中心，因为要探讨两边小的串，所以slow=slow->next
3、两边关于中心点，中心对称，所以需要把右面的串倒转过来，再让fast=head，
4、这样就可以从两个小链表的头，一起往后判断，一旦出现不相等，就是false，全相等，为true
5、结束条件:slow指向空

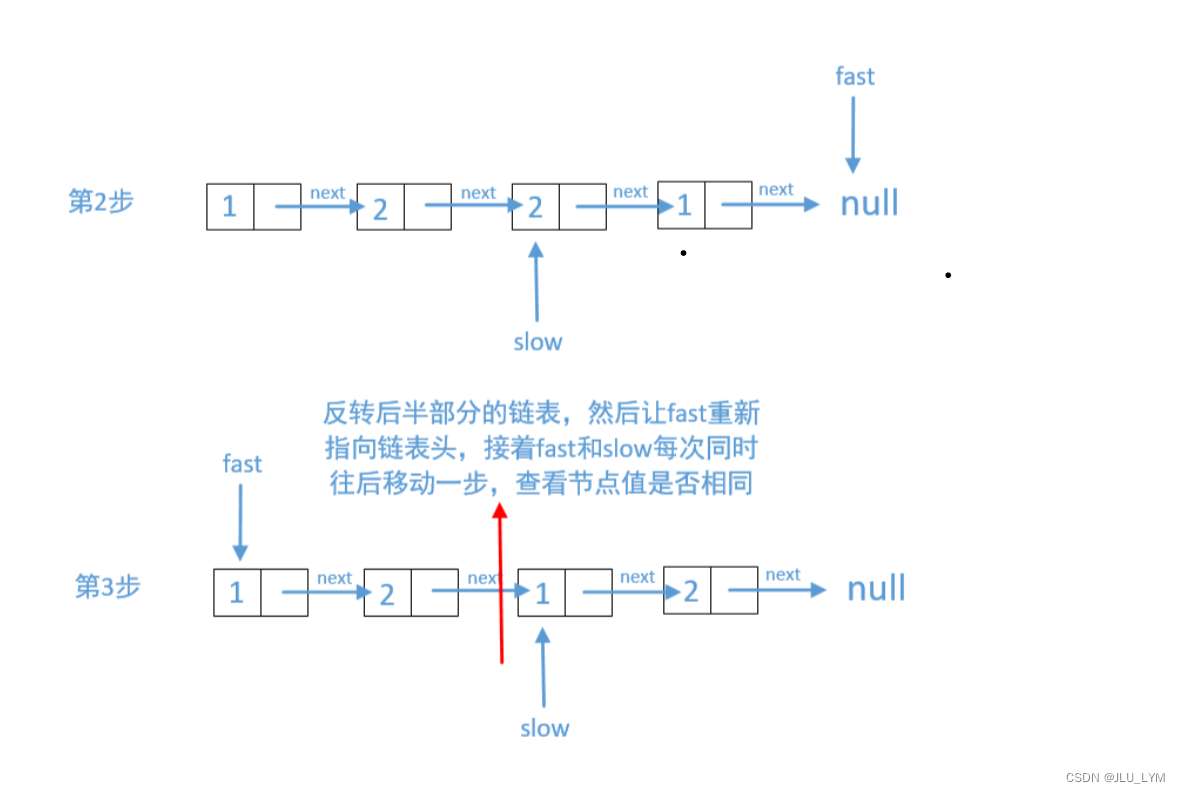
 class Solution {
 public:
	 //这个题实在不会，就得转化成数组，空间复杂度O(n)
	 //1、快慢指针指向中点，把后半段链表标识出来
	 //2、反转后半段
	 //3、从头开始挨个比较
	 bool isPalindrome(ListNode* head) {
		 ListNode *fast = head, *slow = head;
		 while (fast != nullptr&&fast->next != nullptr) {//fast连跳两次,注意边界
			 fast = fast->next->next;
			 slow = slow->next;
		 }
		 //这个自己画一下就可以区别
		 //fast不空，奇数个元素，反之偶数个元素
		 //奇数个元素，slow指的恰好就是回文中心，需要把后面的部分给反转，偶数个元素，指向的恰好就是需要反转的后半部分链表
		 if (fast != nullptr) {
			 slow = slow->next;
		 }
		 slow = Reverse(slow);
		 fast = head;
		 while (slow != nullptr) {//现在还是一个链表，所以slow最后会指空
			 if (fast->val != slow->val) {
				 return false;
			 }
			 slow = slow->next;
			 fast = fast->next;
		 }
		 return true;
	 }
 private:
	 //链表反转,头插法就行
	 ListNode* Reverse(ListNode* l) {
		 ListNode* head = new ListNode();
		 ListNode* p = l;
		 while (p != nullptr) {
			 ListNode* tmp = p;
			 p = p->next;
			 tmp->next = head->next;
			 head->next = tmp;
		 }
		 return head->next;
	 }
 };