【数据结构与算法】时间复杂度和空间复杂度

🔥 本文由 程序喵正在路上 原创，CSDN首发！
💖 系列专栏：数据结构与算法
🌠 首发时间：2022年9月16日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生

前言

我们如何判断一个算法的好坏？我们如何比较不同算法？

算法复杂度

算法的复杂性体现在运行该算法时所有占用计算机资源的多少上，计算机最重要的资源是时间（CPU）和空间（内存），因此复杂度分为时间和空间复杂度

渐进时间复杂度是指执行算法所需要的计算工作量；而空间复杂度是指执行这个算法所需要的内存空间

时间复杂度

时间复杂度最简单的描述就是计算机运行算法时，程序代码被执行的总次数，而程序代码的执行总次数一般与问题规模（需要处理的数据量）有关

一般情况下，算法中基本语句重复执行的次数是问题规模 n 的某个函数 f(n)，算法的时间量度记作 T(n) = O(f(n))，T 表示 time，它表示随问题规模 n 的增大，算法执行时间的增长率和 f(n) 的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度

普通函数

我们来看下面这段代码

int sum(int n)
{
	int value = 0;
	int i = 1;
	while (i <= n) 
	{
		value += i;
		i++;
	}
	return value;
}
1
2
3
4
5
6
7
8
9
10
11

我们假设传入的 n=100，那么程序将会被执行 1+1+100+100+100+1=303 次，也就是 3n+3 次，记作 T(n) = O(3n+3)

时间复杂度关心的是数量级，所以我们要对 f(n) 函数表达式进行简化，具体的原则是：

• 略去常数
• 只保留最高阶的项
• 变最高阶项的系数为 1

也就是说对于普通的函数，我们只需要关心代码中最内层循环的次数就 OK 了

所以前面那段代码的时间复杂度写为 O(n) 即可

常见的时间复杂度按数量级递增排列依次为：常量阶 O(1)、对数阶 O(log₂n)、线性阶 O(n)、线性对数阶 O(nlog₂n)、平方阶 O(n²)、立方阶 O(n³)、… 、k 次方阶 O(n^k)、指数阶 O(2ⁿ) 等等

O(1) < O(log₂n) < O(n) < O(nlog₂n) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

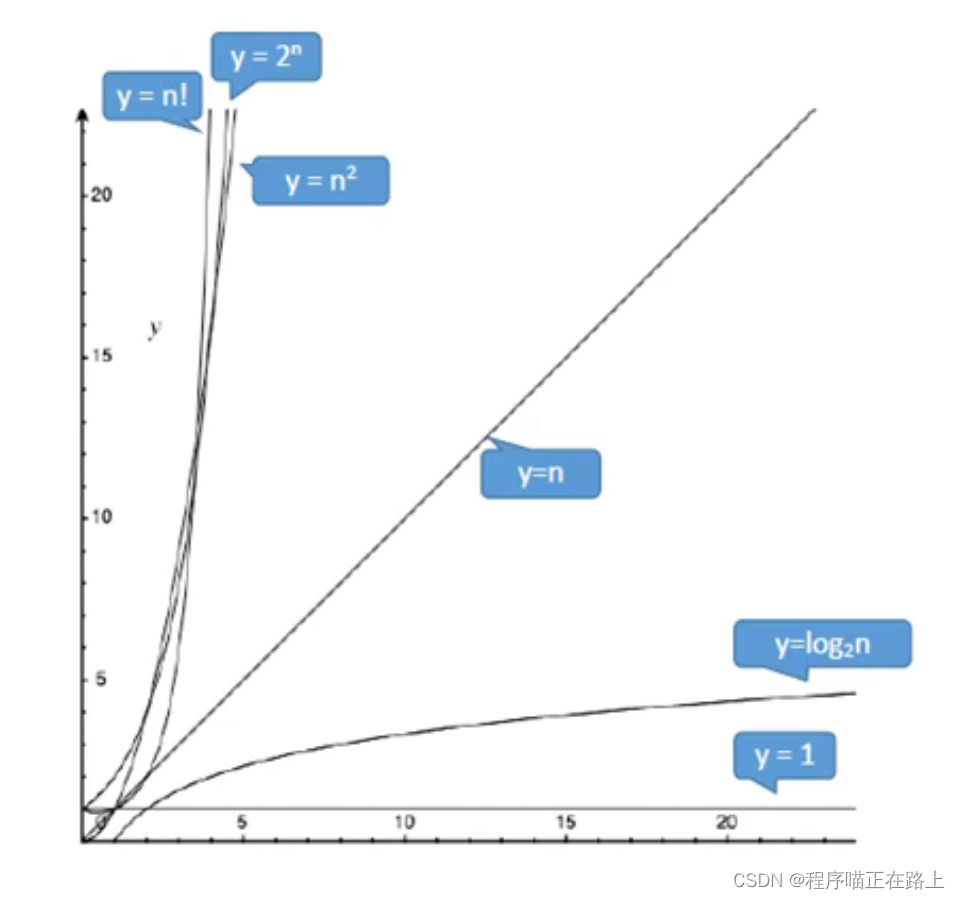
注意：

1. 别把 log₂n 当成系数
2. 如果输入的参数有两个 m 和 n，时间复杂度可以表示为 O(max(m, n))、O(max(m², n²))

时间复杂度有 最好时间复杂度、最坏时间复杂度 和 平均时间复杂度 之分，通常我们只讨论算法在最坏情况下的时间复杂度，即分析在最坏情况下，算法执行时间的上界

递归函数

对于递归函数，我们不仅要关心它最内层循环的次数，还要关心它递归的次数

• 下面这个递归函数的时间复杂度为 O(1) * O(n)，也就是 O(n)

  int sum(int n)
  { 
  	if (n == 0) return 0;
  	return n + sum(n - 1);
  }
  1
  2
  3
  4
  5

• 下面这个递归函数的时间复杂度为 O(n) * O(n/2)，也就是 O(n²)

  int sum(int n)
  {
  	if (n == 0) return 0;
  	
  	int value = 0;
  	int i = 1;
  	while (i <= n) 
  	{
  		value += i;
  		i++;
  	}
  	
  	return value + sum(n - 1);
  }
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14

常见的时间复杂度

• O(1)

  int x = 0;
  int y = 1;
  int temp = x;
  x = y;
  y = temp;
  1
  2
  3
  4
  5

• O(n)

  for (int i = 1; i <= n; i++) {
  	x++;
  }
  1
  2
  3

• O(logN)

  int i = 1;
  while (i < n) {
  	i *= 2;
  }
  1
  2
  3
  4

• O(nlogN)

  for (int i = 1; i <= n; i++) {
  	int x = 1;
  	while (x < n) {
  		x *= 2;
  	}
  }
  1
  2
  3
  4
  5
  6

• O(n²)

  for (int i = 1; i <= n; i++) {
  	for (int j = 1; j <= n; j++) {
  		x++;
  	}
  }
  1
  2
  3
  4
  5

空间复杂度

空间复杂度 S(n) 是指算法消耗的内存空间，也是问题规模（需要处理的数据量）n 的函数，S(n) = O(f(n))，S 表示 space

普通函数

还是这段代码

int sum(int n)
{
	int value = 0;
	int i = 1;
	while (i <= n) 
	{
		value += i;
		i++;
	}
	return value;
}
1
2
3
4
5
6
7
8
9
10
11

不管 n 怎么变，算法所需要的内存空间都是一个固定的常数，空间复杂度为 S(n) = O(1)

然后我们再来看下面这个函数

int sum(int n)
{
	int i;
	int arr[n];

	...
}
1
2
3
4
5
6
7

如果 int 占用的内存是 4B，这个函数所需空间是 4+4+4n，所以 S(n) = O(n)

int sum(int n)
{
	int i;
	int arr1[n];
	int arr2[n][n];

	...
}
1
2
3
4
5
6
7
8

这个函数所需空间是 4+4+4n+4n²，所以 S(n) = O(n²)

递归函数

递归函数嵌套地调用自己，函数的参数和局部变量占用的内存空间在递去的过程中会持续增长，在归来的时候才逐层释放。当递归的深度达到一定量级，可能会造成栈内存空间不足的情况

int sum(int n)
{
	if (n == 0) return 0;
	int i, j, k;
	return n + sum(n - 1);
}
1
2
3
4
5
6

4 个变量，递归的深度为 n，所以空间复杂度为 O(4n)，即 O(n)

再来看一下下面这两个有意思的例子

• 空间复杂度为 O(n)*O(n/2) = O(n²/2)，即 O(n²)

  int sum(int n)
  {
  	if (n == 0) return 0;
  	int arr[n];
  	int value = n + sum(n - 1);
  	return value;
  }
  1
  2
  3
  4
  5
  6
  7

• 空间复杂度为 O(n)+O(n/2) = O(3n/2)，即 O(n)

  int sum(int n)
  {
  	if (n == 0) return 0;
  	int value = n + sum(n - 1);
  	int arr[n];
  	return value;
  }
  1
  2
  3
  4
  5
  6
  7