-
记录:2022-9-15 罗马数字转正数 组合总和 分割回文串 信号量算法代码 文件共享 一致性语义 文件保护 文件系统结构
学习时间:2022-9-15
学习内容
1、leetCode 一道简单题 两道中等回溯题
罗马数字转正数
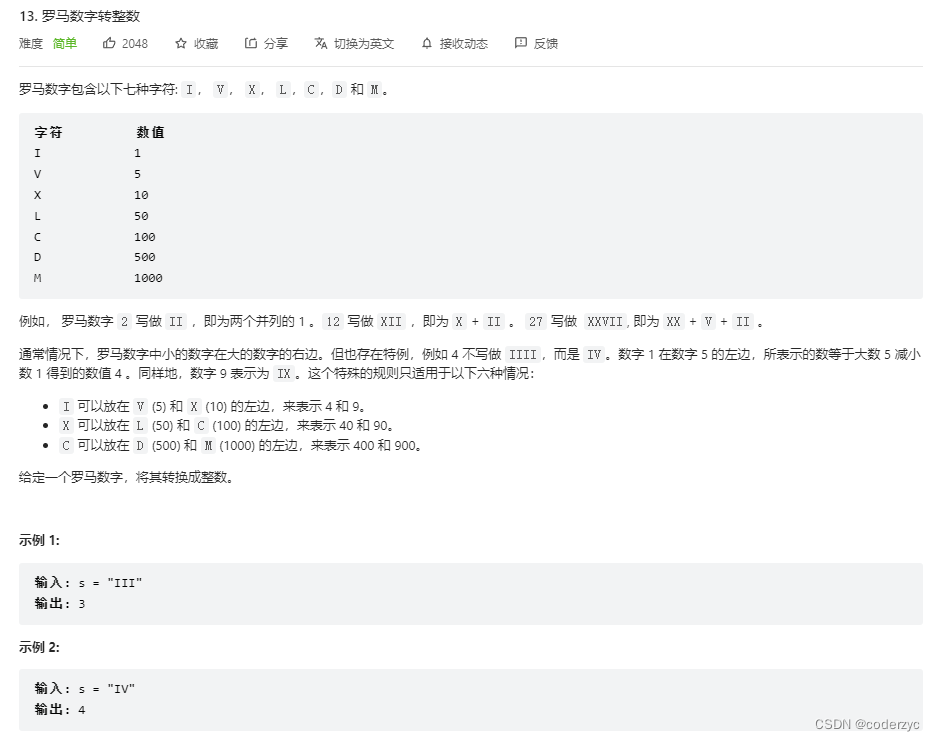
class Solution { public int romanToInt(String s) { int index = s.length()-1; int ans = 0; while(index>=0){ if(index > 0){ String subStr = s.substring(index-1,index+1); if(getCharValue(subStr) != -1){ ans+=getCharValue(subStr); index-=2; }else{ ans+=getCharValue(s.substring(index,index+1)); index--; } }else{ ans+=getCharValue(s.substring(0,1)); index--; } } return ans; } //用表代替hash,节约内存,并且时间按复杂度O1 public int getCharValue(String s){ if(s.equals("I")){ return 1; } if(s.equals("V")){ return 5; } if(s.equals("X")){ return 10; } if(s.equals("L")){ return 50; } if(s.equals("C")){ return 100; } if(s.equals("D")){ return 500; } if(s.equals("M")){ return 1000; } if(s.equals("IV")){ return 4; } if(s.equals("IX")){ return 9; } if(s.equals("XL")){ return 40; } if(s.equals("XC")){ return 90; } if(s.equals("CD")){ return 400; } if(s.equals("CM")){ return 900; } return -1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
代码偏长,原因是为了替换HashMap而使用打表的方式,空间复杂度确实不高,但是时间复杂度高了,原因是因为大量运用substring字符串操作,导致效率较低,可以把String替换成Char的Array,应该可以降低复杂度
组合总和

回溯第二题class Solution { int sum = 0; Stack<Integer> stack = new Stack<Integer>(); List<List<Integer>> result = new ArrayList<List<Integer>>(); public List<List<Integer>> combinationSum(int[] candidates, int target) { //对candidates排序,以便后续剪枝 Arrays.sort(candidates); backtracing(target,candidates,0); return result; } public void backtracing(int target,int[] candidates,int startIndex){ if(sum == target){ //收集结果并弹出 result.add(new ArrayList(stack)); return; } if(sum > target){ return;//超过了,直接弹出 } for(int i = startIndex;i<candidates.length;i++){ //剪枝 if(candidates[i] + sum > target){ break; } sum+=candidates[i]; stack.push(candidates[i]); backtracing(target,candidates,i); sum-=candidates[i]; stack.pop(); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
与昨天的回溯类似的类型,难度不算大,递归终止条件:判断sum是否大于target
分割回文串

这道题对我来说难点在于如何去寻找分割点,看懂了这道题就和前面那个差不多
分割点为:String subStr = s.substring(startIndex,i);
class Solution { int n; boolean[][] part; List<List<String>> list = new ArrayList<List<String>>(); List<String> ans = new ArrayList<String>(); public List<List<String>> partition(String s) { n = s.length(); part = new boolean[n+1][n+1]; for(int i=0;i<n;i++){ Arrays.fill(part[i],true); } for(int i=n-1;i>=0;i--){ for(int j= i+1;j<n;j++){ part[i][j] = (s.charAt(i) == s.charAt(j)) && part[i+1][j-1]; } } dfs(s,0); return list; } public void dfs(String s, int i){ if(i == n){ list.add(new ArrayList<String>(ans)); } for(int j=i;j<n;j++){ if(part[i][j]){ ans.add(s.substring(i,j+1)); dfs(s,j+1); ans.remove(ans.size()-1); } } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
复杂度偏高,附一个低复杂度代码
class Solution { int n; boolean[][] part; List<List<String>> list = new ArrayList<List<String>>(); List<String> ans = new ArrayList<String>(); public List<List<String>> partition(String s) { n = s.length(); part = new boolean[n+1][n+1]; for(int i=0;i<n;i++){ Arrays.fill(part[i],true); } for(int i=n-1;i>=0;i--){ for(int j= i+1;j<n;j++){ part[i][j] = (s.charAt(i) == s.charAt(j)) && part[i+1][j-1]; } } dfs(s,0); return list; } public void dfs(String s, int i){ if(i == n){ list.add(new ArrayList<String>(ans)); } for(int j=i;j<n;j++){ if(part[i][j]){ ans.add(s.substring(i,j+1)); dfs(s,j+1); ans.remove(ans.size()-1); } } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
信号量算法代码
信号量代码示意图如下(按顺序执行):
bread(int dev,int block){ struct buffer_head *bh; ll_rw_block(READ,bh); wait_on_buffer(bh); }- 1
- 2
- 3
- 4
- 5
sys_sem_wait(int sd){ cli(); if(setable[sd].value-- < 0){ 设置自己为阻塞,将自己加入semtable[sd]的queue中; schedule(); } sti();//完成中断,可以被其他进程占用 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
lock_buffer(buffer_head* bh){ cli();//硬件上锁 while(bh->b_lock){ sleep_on(&bh->b_wait);//这里while,每次锁结束后,循环进入sleep_on中,挨个唤醒进程,这样做的目的是为了让每个进程都可以通过优先级的方式被调度,而不单纯是依靠队首pop } bh->b_lock = 1; sti();//完成中断,可以被其他进程占用 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
void sleep_on(struct task_struct **p){ struct task_struct *tmp; tmp = *p; *p = current; current->state = TASK_UNINTERRUPTIBLE; schedule(); if(tmp){ tmp->state = 0; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
void unlock_buffer(struct buffer_head * bh){ bh->b_block = 0; wake_up(&bh->b_wait); }- 1
- 2
- 3
- 4
void wake_up(struct task_struct **p){ if(p&& *p){ (**p).state=0; *p=NULL; } }- 1
- 2
- 3
- 4
- 5
- 6
文件系统:文件共享|一致性语义|保护
文件共享
文件共享需要考虑两个方面:
- 如何共享到多个文件系统
- 如何解决冲突操作
多用户
多用户系统大多数采用用户与组的概念,所有者可以对文件执行所有操作,文件组的成员只能执行这些操作的子集。
远程文件系统
远程共享方式有三种
- 分布式文件系统
- ftp
- fip(匿名访问,如在浏览器上进行文件传输)
客户机-服务器模型
包含文件的机器是服务器,访问文件的机器是客户机(图床服务器是这种结构?)
分布式文件系统
为了更加方便的管理客户机-服务器系统,采用分布式信息系统。
他可以对远程计算信息提供统一访问。
目前可以采用轻量级目录访问协议,这种协议作为安全的分布式命名机制,这种协议的结果是单点登录,一处获得了认证后处处可以使用。一致性语义
一致性语义用于评估文件共享的文件系统
介绍了两种语义:
unix语义- 一个用户对已经打开文件的写入,对于打开同一个文件的其他用户立即可见
- 一种共享模式允许用户共享文件的当前位置指针。一个用户前移指针会影响所有的共享用户
会话语义
- 一旦一个用户对打开文件进行写入,对于其他打开同一文件的其他用户,不是立即可见的
- 一旦文件关闭,对其做的更改只有后来打开的会话可见,已打开的文件实例不反映这些变化
保护
主要有两点保护,一是可靠性,二是非法访问问题
1、操作保护
通过限制用户的操作来进行保护(受控访问)
2、身份控制
根据用户身份控制访问。最普遍的实现方法为:为每个文件和目录关联一个访问控制列表,以指定每个用户的名称以及其允许访问的类型,当请求特定文件时,操作系统将会检查该文件关联的访问列表
3、加密
对文件增加密码文件系统的实现
实现一个文件系统,主要考虑三方面问题:存储,访问,性能
文件系统的结构
文件系统本身可以由很多不同的层分层设计,每层设计可以利用更底层的功能,创建新的功能,用于更高级的服务
下图是一种可实现的分层设计方式: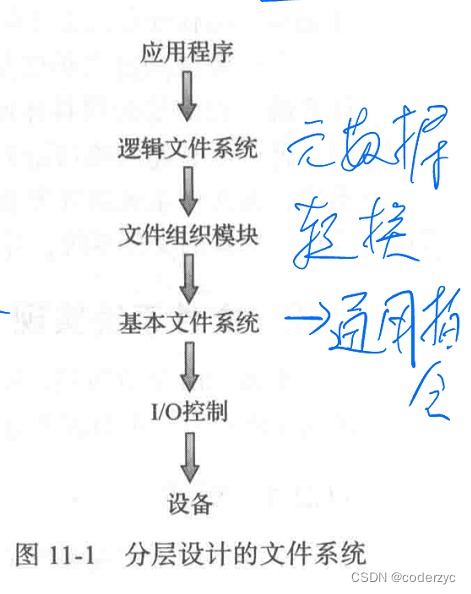
这种设计将逻辑文件与物理文件之间以文件组织模块相隔
逻辑文件系统管理的是元数据信息,包括文件系统的所有结构,而不包括实际数据。逻辑文件管理目录结构,并且逻辑文件系统还负责保护
文件组织模块知道文件及其逻辑块和物理块,该模块可以将逻辑块转换成物理块
基本文件系统负责各种通用指令,以读取和写入磁盘的物理块,也负责管理内存缓冲区和保存各种文件系统、目录和数据块的缓存。
I/O控制包括设备驱动程序和中断处理程序,以在主内存和磁盘系统之间传递信息。 -
相关阅读:
夯实算法-跳跃游戏
最强总结!18个机器学习核心算法模型!!
软件开发中,做好需求管理,这4点很关键。
Motion Plan之搜索算法笔记
国际结算重点知识整理
墨天轮“高可用架构”干货文档分享(含Oracle、MySQL、PG资料124篇)
SaaSBase:什么是有道云笔记?
力扣每日练习3.10
索引生命周期管理ILM看完不懂你锤我
【软件工程】软件工程之道—《人月神话》读后思考
- 原文地址:https://blog.csdn.net/qq_44686225/article/details/126879609
