骑士周游算法（Java）

第9章 骑士周游问题

9.1 马踏棋盘游戏

1）马踏棋盘算法也被称为骑士周游问题

2）将马随机放在国际象棋的8*8棋盘上Board[0~7] [0~7]的某个方格中，马按照走棋规则（马走日字）进行移动。要求每个方格只进行一次，走遍棋盘上全部64各方格

9.2 骑士周游回溯算法简介

1）马踏棋盘（骑士周游问题）实际上是图的深度优先搜索（DFS）的应用

2）如果使用回溯（深度优先搜索）来解决，假如马走了53个点，如图：坐标（1，0）发现已经走到尽头，没有办法继续回退，查看其他路径，就在棋盘上不停的回溯，

3）分析第一种方式的问题，使用贪心算法（greedyAlgorithm）进行优化，解决马踏棋盘问题

后续会用贪心算法优化

9.3 代码实现

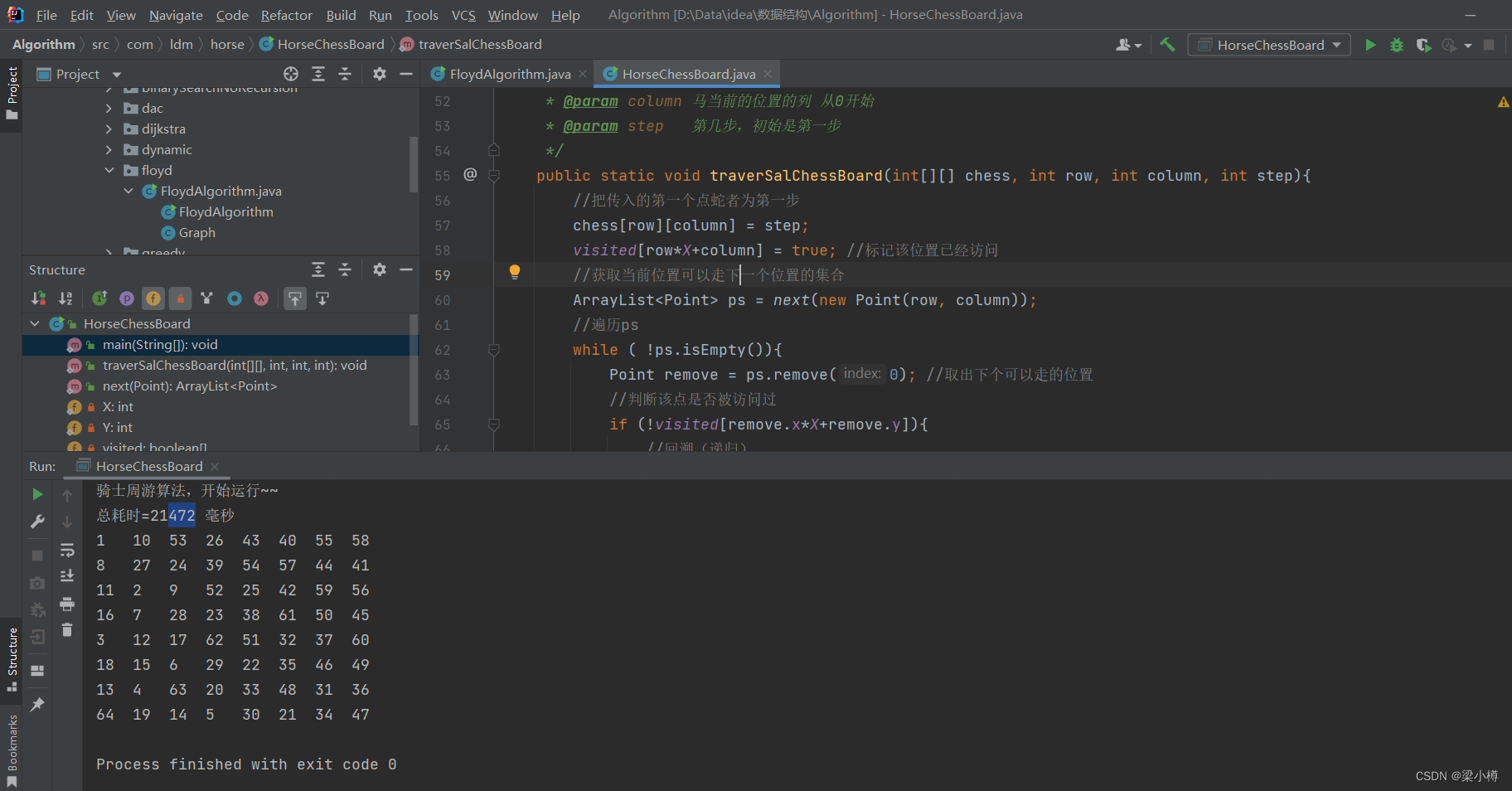
没有使用贪心算法花费21秒走完

package com.ldm.horse;

import java.awt.*;
import java.util.ArrayList;

/**
 * @author 梁东明
 * 2022/9/15
 * 人生建议：看不懂的方法或者类记得CTRL + 点击 看看源码或者注解
 * 点击setting在Editor 的File and Code Templates 修改
 */
public class HorseChessBoard {
    private static int X; //棋盘的列数
    private static int Y; //棋盘的行数
    //创建一个数组，标记棋盘的各个位置是否被访问过
    private static boolean visited[];
    //使用一个属性，标记是否棋盘的所有位置都被访问
    private static boolean finished; // 如果为true,表示成功

    public static void main(String[] args) {
        System.out.println("骑士周游算法，开始运行~~");
        //测试骑士周游算法是否正确
        X = 8;
        Y = 8;
        int row = 1; //马儿初始位置的行，从1开始编号
        int column = 1; //马儿初始位置的列，从1开始编号
        //创建棋盘
        int[][] chessBoard = new int[X][Y];
        visited = new boolean[X*Y];
        //测试一下耗时
        long start = System.currentTimeMillis();
        traverSalChessBoard(chessBoard,row-1,column-1,1);
        long end = System.currentTimeMillis();
        System.out.println("总耗时="+(end-start)+" 毫秒");

        //输出棋盘的情况
        for (int[] rows : chessBoard) {
            for (int step : rows) {
                System.out.print(step +"\t");
            }
            System.out.println();
        }


    }

    /**
     * 骑士周游算法实现
     *
     * @param chess  棋盘
     * @param row    马当前的位置的行 从0开始
     * @param column 马当前的位置的列 从0开始
     * @param step   第几步，初始是第一步
     */
    public static void traverSalChessBoard(int[][] chess, int row, int column, int step){
        //把传入的第一个点蛇者为第一步
        chess[row][column] = step;
        visited[row*X+column] = true; //标记该位置已经访问
        //获取当前位置可以走下一个位置的集合
        ArrayList<Point> ps = next(new Point(row, column));
        //遍历ps
        while ( !ps.isEmpty()){
            Point remove = ps.remove(0); //取出下个可以走的位置
            //判断该点是否被访问过
            if (!visited[remove.x*X+remove.y]){
                //回溯（递归）
                traverSalChessBoard(chess, remove.x, remove.y, step+1);
            }
        }
        //判断马儿是否完成了任务，使用   step 和应该走的步数比较 ，
        //如果没有达到数量，则表示没有完成任务，将整个棋盘置0
        //说明: step < X * Y  成立的情况有两种
        //1. 棋盘到目前位置,仍然没有走完
        //2. 棋盘处于一个回溯过程
        if ( step < X*Y && !finished){
            chess[row][column] = 0;
            visited[row*X+column] = false;
        }else {
            finished = true;
        }
    }
    /**
     * 功能： 根据当前位置(Point对象)，计算马儿还能走哪些位置(Point)
     * 并放入到一个集合中(ArrayList), 最多有8个位置
     * @param curPoint
     * @return
     */
    public static ArrayList<Point> next(Point curPoint){
        //创建一个ArrayList
        ArrayList<Point> ps = new ArrayList<>();
        //创建一个Point
        Point p1 = new Point();
        //表示马儿可以走5这个位置
        if((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y -1) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走6这个位置
        if((p1.x = curPoint.x - 1) >=0 && (p1.y=curPoint.y-2)>=0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走7这个位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走0这个位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走1这个位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走2这个位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走3这个位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走4这个位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));
        }
        return ps;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128

使用贪心算法优化 17毫秒走完

package com.ldm.horse;

import java.awt.*;
import java.util.ArrayList;
import java.util.Comparator;

/**
 * @author 梁东明
 * 2022/9/15
 * 人生建议：看不懂的方法或者类记得CTRL + 点击 看看源码或者注解
 * 点击setting在Editor 的File and Code Templates 修改
 */
public class HorseChessBoard {
    private static int X; //棋盘的列数
    private static int Y; //棋盘的行数
    //创建一个数组，标记棋盘的各个位置是否被访问过
    private static boolean visited[];
    //使用一个属性，标记是否棋盘的所有位置都被访问
    private static boolean finished; // 如果为true,表示成功

    public static void main(String[] args) {
        System.out.println("骑士周游算法，开始运行~~");
        //测试骑士周游算法是否正确
        X = 8;
        Y = 8;
        int row = 1; //马儿初始位置的行，从1开始编号
        int column = 1; //马儿初始位置的列，从1开始编号
        //创建棋盘
        int[][] chessBoard = new int[X][Y];
        visited = new boolean[X*Y];
        //测试一下耗时
        long start = System.currentTimeMillis();
        traverSalChessBoard(chessBoard,row-1,column-1,1);
        long end = System.currentTimeMillis();
        System.out.println("总耗时="+(end-start)+" 毫秒");

        //输出棋盘的情况
        for (int[] rows : chessBoard) {
            for (int step : rows) {
                System.out.print(step +"\t");
            }
            System.out.println();
        }


    }

    /**
     * 骑士周游算法实现
     *
     * @param chess  棋盘
     * @param row    马当前的位置的行 从0开始
     * @param column 马当前的位置的列 从0开始
     * @param step   第几步，初始是第一步
     */
    public static void traverSalChessBoard(int[][] chess, int row, int column, int step){
        //把传入的第一个点蛇者为第一步
        chess[row][column] = step;
        visited[row*X+column] = true; //标记该位置已经访问
        //获取当前位置可以走下一个位置的集合
        ArrayList<Point> ps = next(new Point(row, column));

        //对ps进行排序,排序的规则就是对ps的所有的Point对象的下一步的位置的数目，进行非递减排序
        sort(ps);
        //遍历ps
        while ( !ps.isEmpty()){
            Point remove = ps.remove(0); //取出下个可以走的位置
            //判断该点是否被访问过
            if (!visited[remove.x*X+remove.y]){
                //回溯（递归）
                traverSalChessBoard(chess, remove.x, remove.y, step+1);
            }
        }
        //判断马儿是否完成了任务，使用   step 和应该走的步数比较 ，
        //如果没有达到数量，则表示没有完成任务，将整个棋盘置0
        //说明: step < X * Y  成立的情况有两种
        //1. 棋盘到目前位置,仍然没有走完
        //2. 棋盘处于一个回溯过程
        if ( step < X*Y && !finished){
            chess[row][column] = 0;
            visited[row*X+column] = false;
        }else {
            finished = true;
        }
    }
    /**
     * 功能： 根据当前位置(Point对象)，计算马儿还能走哪些位置(Point)
     * 并放入到一个集合中(ArrayList), 最多有8个位置
     * @param curPoint
     * @return
     */
    public static ArrayList<Point> next(Point curPoint){
        //创建一个ArrayList
        ArrayList<Point> ps = new ArrayList<>();
        //创建一个Point
        Point p1 = new Point();
        //表示马儿可以走5这个位置
        if((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y -1) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走6这个位置
        if((p1.x = curPoint.x - 1) >=0 && (p1.y=curPoint.y-2)>=0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走7这个位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走0这个位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走1这个位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走2这个位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走3这个位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));
        }
        //判断马儿可以走4这个位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));
        }
        return ps;
    }

    //根据当前这个一步的所有的下一步的选择位置，进行非递减排序, 减少回溯的次数
    public static void sort(ArrayList<Point> ps){
        ps.sort(new Comparator<Point>() {
            @Override
            public int compare(Point o1, Point o2) {
                //先获取o1的下一步的位置个数
                int count1 = next(o1).size();
                //再获取o2的下一步的位置个数
                int count2 = next(o2).size();
                if ( count1 < count2 ){
                    return -1;
                }else if ( count1 == count2){
                    return 0;
                }else {
                    return 1;
                }

            }
        });
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153

本次骑士周游算法算法 的教程出自韩顺平的数据结构与算法

数据结构和算法教程，哔哩哔哩详细教程
在 189-194p.

相信有不少朋友是从B站过来的吧！我在弹幕里承诺过会把韩老师的数据结构与算法系列全部更新，2022.8.18开始，中途因为中秋回家休息两天，到2022.9.15结束，每天花5、6个小时看完8个视频左右，跟着老师敲代码。今天终于更新完了。很不舍得，要和大家分别啦！我的数据结构系列文章是按照韩老师的教学基础下，增加了我自己大量的心血，因为教程是三年前的，还是用eclipse写的（我的使用idea）所以韩老师的代码不免在细节上有挺多的瑕疵，我都一一在自己系列文章中加以改正，添加我自己的注解以及建议。以及很多idea快捷键的使用技巧。到现在我都不敢相信我真的坚持下来了，所以很想说一句：希望大家以后在学习的路上能一直坚持，借用韩老师的桌面名言：除非我不想赢，不然没人能让我输

这里是我学习数据结构的全部笔记和代码（使用idea编辑器写的）。大家有兴趣的可以下载来参考

点击下载

最后，认识一下，我是小白。努力成为一名合格的程序员。期待与你的下次相遇