Bresenham直线生成算法详解

基本思想

        比较从理想直线到位于直线上方的像素的距离t和相邻的位于直线下方的像素的距离s，根据距 离误差项的符号确定与理想直线最近的像素，如下图所示：

判断 s-t 的大小

        已知当前的像素的中心点坐标为（xi,yi）,根据 s-t 的值来判断下一步的点所在位置。详细计算推导过程如下：

 设位于s、t之间直线的坐标（x,y），得到  ，

 

   时，真实的直线y值为： ，

 

 m代表直线的斜率(slope)，故,

  在原式两边同时乘上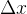，原式 = ，

 我们的目的是判断 s-t 是大于0的还是小于0的，且由于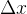恒大于0，所以我们可以令

 ，此时  与s-t 正负方向一致，可以用来代替 s-t 来判断其大小。由于判断的是正负性，所以一些已知项可以当成常数C来看。

 

此时

联立两个式子，注意代入 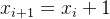，然后求  ，结果得到：

 当我们选择直线上方的点的话，那么  ，，此时

 ；

反之 。

 最终推出以下式子：

此时  就代表了  的正负性，当  ，代表了 s 比 t 大，所以要取上面的一格，即 ; 反之取的格子位置不变，即  。

接下来看一道例题，来体会一下breseham算法的应用。

例题

首先先画好直线段：

接着通过求 三个变量的值来确定像素的坐标位置：

第一个像素点位置就是起点，即(0,0)，

初始的误差值 ，由前面的式子 ，令 i = 1，

得:

 

所以得值  =  = -1。

综上第一个点，三个参数是。

第二个点，x一定往右一格，所以此时。

因为上一格求得的误差，所以此时 ，即。

由于，故 。

综上第二个点，三个参数是。

第三个点，x一定往右一格，所以此时。

因为上一格求得的误差，所以此时 ，即。

由于，故 。

综上第三个点，三个参数是。

依次类推······

结果如图：

 得到的坐标依次为(0,0) (1,0) (2,1) (3,1) (4,2) (5,2)。

根据坐标填充像素：

 此时，breseham算法生成直线像素已完成。

代码描述(C语言伪代码)

//Bresenham
void Bes_line(int x0,int y0,int x1,int y1){
	int dx,dy,h,x,y;
	dx=abs(x0-x1);
	dy=abs(y0-y1);
	h=2*dy-dx;
	x=x0;
	y=y0;
 
	glColor3f(1.0, 0.0, 0.0);
    glBegin(GL_POINTS);  
    glVertex2f(x,y);	
	while (x
	{
		if(h<0)  h+=2*dy;
		else{
			h=+2*(dy-dx);
			y++;
		}
		glVertex2f(x,y);		
		x++;
	}
	glEnd();
}

Bresenham算法的优点

• 不用计算斜率，不涉及到浮点数的运算。 

• 计算中涉及到的全部是整数

• 乘法运算只有乘以2，可以用移位运算来实现。