-
【深度学习】最大熵马尔科夫、CRF、条件随机场、最大匹配法
一 最大熵马尔科夫和CRF
最大熵模型(MaxEnt):指的是多元逻辑回归
由于等概率的分布具有最大熵,所以最大熵的模型通过词性标注问题来描述就是:
- 在没有任何假设的情况下,认为每种词性的概率都是相同的,假设有10中词性,那么每个词性的概率都是1/10
- 如果语料表明,所有的词语出现的词性只有10个中的4个,那么此时,调整所有词的词性为 A : 1 / 4 , B : 1 / 4 , C : 1.4 , D : 1 / 4 , E : 0.... A:1/4 ,B:1/4,C:1.4,D:1/4,E:0.... A:1/4,B:1/4,C:1.4,D:1/4,E:0....
- 当继续增加语料,发现A和B的概率很高,10次中有8次,某个词的词性不是A就是B,那么此时调整词性概率为: A : 4 / 10 , B : 4 / 10 , C : 1 / 10 , D : 1 / 10 A:4/10,B:4/10,C:1/10,D:1/10 A:4/10,B:4/10,C:1/10,D:1/10
- 重复上述过程
寻找一个熵最大的模型,就是要使用多元逻辑回归,训练他的权重w,让训练数据能够似然度最大化
训练数据能够似然度最大化:训练数据是总体的一个抽样,让训练数据尽可能能够代表总体,从而可以让模型可以有更好的表现力
**最大熵马尔科夫模型(MEMM)**是马尔科夫模型的变化版本。在马尔科夫模型中,使用贝叶斯理论来计算最有可能的观测序列,即:
t ^ n = a r g m a x t n P ( t n ∣ w n ) = a r g m a x t n P ( w i ∣ t i ) P ( t i ∣ t i − 1 ) \hat{t}_n = \mathop{argmax}_{t_n}P(t_n|w_n) = \mathop{argmax}_{t_n}P(w_i|t_i)P(t_i|t_{i-1}) t^n=argmaxtnP(tn∣wn)=argmaxtnP(wi∣ti)P(ti∣ti−1)
但是在MEMM中,直接去计算了后验概率P(t|w),直接对每个观测值的状态进行分类,在MEMM中,把概率进行了拆解:
T ^ = a r g m a x T P ( T ∣ W ) = a r g m a x ∏ i P ( t a g i ∣ w o r d i , t a g i − 1 ) \hat{T} = \mathop{argmax}_T P(T|W) = \mathop{argmax}\prod_i P(tag_i|word_i,tag_{i-1}) T^=argmaxTP(T∣W)=argmaxi∏P(tagi∣wordi,tagi−1)
即:使用前一个状态tag和当前的词word,计算当前tag。和隐马尔可夫模型不同的是,在上述的公式中,对于计算当前tag的分类过程中,输入不仅可以是 w o r d i 和 t a g i − 1 word_i和tag_{i-1} wordi和tagi−1,还可以包含其他的特征,比如:词语的第一个字母是否为大写,词语的后缀类型,前缀类型的等等。
所以MEMM的表现力会比HMM要更好。
二 条件随机场
**条件随机场(conditional random field,CRF)**是有输入x和输出y组成的一种无向图模型,可以看成是最大熵马尔可夫模型的推广。
下图是常用于词性标注的线性链 条件随机场的图结构。其中x是观测序列,Y是标记序列

下图是HMM,MEMM,CRF的对比
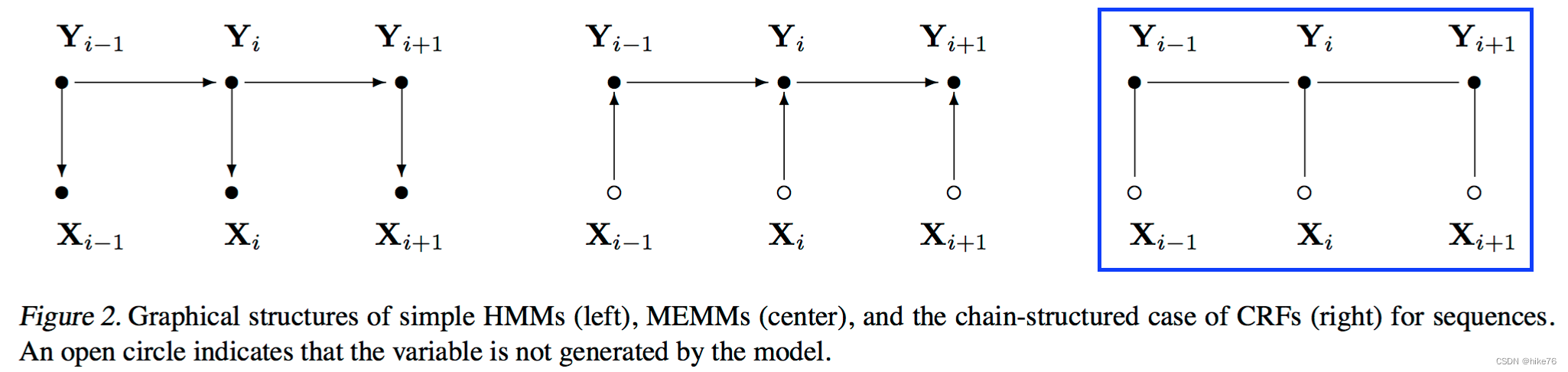
当观测序列为 x = x 1 , x 2 . . . x=x_1,x_2... x=x1,x2... 时,状态序列为 y = y 1 , y 2 . . . . y=y_1,y_2.... y=y1,y2....的概率可写为:
P ( Y = y ∣ x ) = 1 Z ( x ) exp ( ∑ k λ k ∑ i t k ( y i − 1 , y i , x , i ) + ∑ l μ l ∑ i s l ( y i , x , i ) ) Z ( x ) = ∑ y exp ( ∑ k λ k ∑ i t k ( y i − 1 , y i , x , i ) + ∑ l μ l ∑ i s l ( y i , x , i ) ) P(Y=y|x)=\frac{1}{Z(x)}\exp\biggl(\sum_k\lambda_k\sum_it_k(y_{i-1},y_i,x,i)+\sum_l\mu_l\sum_is_l(y_i,x,i)\biggr) \\ Z(x)=\sum_y\exp\biggl(\sum_k\lambda_k\sum_it_k(y_{i-1},y_i,x,i)+\sum_l\mu_l\sum_is_l(y_i,x,i)\biggr) P(Y=y∣x)=Z(x)1exp(k∑λki∑tk(yi−1,yi,x,i)+l∑μli∑sl(yi,x,i))Z(x)=y∑exp(k∑λki∑tk(yi−1,yi,x,i)+l∑μli∑sl(yi,x,i))
其中 Z ( x ) Z(x) Z(x)是归一化因子,类似softmax中的分母,计算的是所有可能的y的和后面的部分由特征函数组成:
转移特征: t k ( y i − 1 , y i , x , i ) t_k(y_{i-1},y_i,x,i) tk(yi−1,yi,x,i) 是定义在边上的特征函数(transition),依赖于当前位置 i 和前一位置 i-1 ;对应的权值为 λ k \lambda_k λk 。
状态特征: s l ( y i , x , i ) s_l(y_i,x,i) sl(yi,x,i) 是定义在节点上的特征函数(state),依赖于当前位置 i ;对应的权值为 μ l \mu_l μl 。
一般来说,特征函数的取值为 1 或 0 ,当满足规定好的特征条件时取值为 1 ,否则为 0 。
对于
北\B京\E欢\B迎\E你\E特征函数可以如下:func1 = if (output = B and feature="北") return 1 else return 0 func2 = if (output = M and feature="北") return 1 else return 0 func3 = if (output = E and feature="北") return 1 else return 0 func4 = if (output = B and feature="京") return 1 else return 0- 1
- 2
- 3
- 4
每个特征函数的权值 类似于发射概率,是统计后的概率。
三 最大匹配法
1 来源
最大匹配法是最简单的分词方法,完全使用词典进行分词,如果词典好,则分词的效果好
2 正向最大匹配法
正向,即从左往右进行匹配
#Maximum Match Method 最大匹配法 class MM: def __init__(self): self.window_size = 4 def cut(self,text): result = [] index = 0 text_lenght = len(text) #研究生命的起源 dic = ["研究","研究生","生命"] while text_lenght >index: #range(3,0,-1) for size in range(min(self.window_size+index,text_lenght),index,-1): piece = text[index:size] print("size:", size,piece) if piece in dic: index = size-1 break index = index+1 #第一次结束index = 3 result.append(piece) print(result) return result- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
逆向最大匹配法
逆向即从右往左进行匹配
#RMM:Reverse Maxmium Match method 逆向最大匹配 class RMM: def __init__(self): self.window_size = 3 def cut(self,text): result = [] index = len(text) #研究生命的起源 dic = ["研究","研究生","生命"] while index>0: for size in range(max((index-self.window_size),0),index): piece = text[size:index] print("size:", size,piece) if piece in dic: index = size+1 print("index:", index) break print("index:",index) index = index - 1 result.append(piece) result.reverse() print(result) return result- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
双向最大匹配法
同时根据正向和逆向的结果,进行匹配
class MCut(): def __init__(self): self.mm = MM() self.rmm = RMM() def cut(self,sentence): """ 1. 词语数量不相同,选择分词后词语数量少的 2. 如果词语数量相同,返回单字数量少的 """ mm_ret = self.mm.cut(sentence) rmm_ret = self.rmm.cut(sentence) if len(mm_ret)==len(rmm_ret): mm_ret_signle_len = len([i for i in mm_ret if len(i)==1]) rmm_ret_signle_len = len([i for i in rmm_ret if len(i)==1]) return mm_ret if rmm_ret_signle_len>mm_ret_signle_len else rmm_ret else: return mm_ret if len(mm_ret)<len(rmm_ret) else rmm_ret- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
-
相关阅读:
详细Spring学习笔记,初识Spring家族
Promise的面试题考点
第十五届蓝桥杯模拟赛【第三期】Java
我的CS Master毕业之路|猿创征文
MyBatis的缓存问题
【HTML5】登录页面制作简易版
牛客网——扫雷
在 Android 应用程序开发期间减少 Android 应用程序大小的 9 种方法
两日总结十三
Linux查找命令
- 原文地址:https://blog.csdn.net/weixin_43923463/article/details/126818100
