浮点数存储规则

二进制小数

首先让我们来看看二进制表示法。二进制表示法使用如下的形式表示：

$b_m{b}_{m-1}\cdots b_1{b}_0.b_{-1}{b}_{-2}\cdots b_{-n}$

其中每个二进制数 $b_i$ 的取值是 0 或 1。

这种表示方法表示的数 $b$：$$\sum _{i=-n}^m{2}^i\times b_i$$

数字的权的定义与二进制小数点符号相关，这意味着小数点左边的数字的权是 2 的正幂，得到整数值；而小数点右边的数字的权是 2 的负幂，得到小数值。

例如，$101.11_2$ 表示数字 $1\times 2^2+0\times 2^1+1\times 2^0+1\times 2^{-1}+2\times 2^{-2}=4+0+1+\frac{1}{2}+\frac{1}{4}=5\frac{3}{4}$

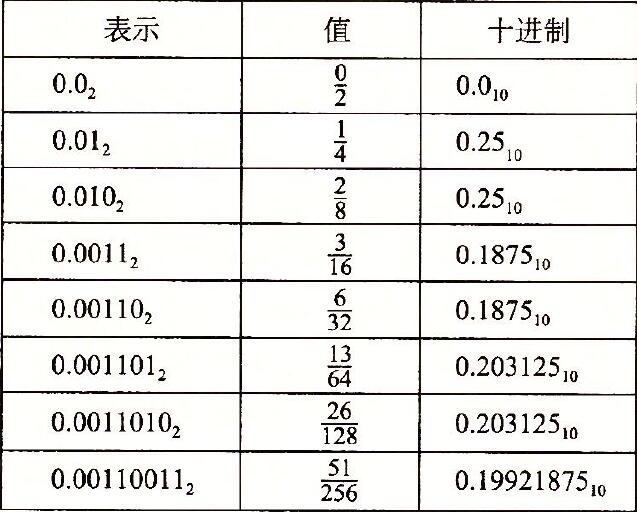
假定我们仅考虑有限长度的编码，那么二进制表示法不能准确地表达像 $\frac{1}{3}$ 和 $\frac{4}{7}$ 这样的数。小数的二进制表示法只能标识那些能被写成 $x\times 2^y$ 的数，其他的值只能被近似的表示。例如，数字 $\frac{1}{5}$ 可以用十进制小数 $0.20$ 精确表示。不过，我们并不能把它准确地表示为一个二进制小数，我们只能近似地表示它，增加二进制表示的长度可以提高表示的精度：

IEEE 浮点表示

IEEE 754 浮点标准用 $V=(-1{)}^S\times M\times 2^E$ 的形式表示一个数：

• 符号 s（sign）决定数的正负
  • 当 s = 0 时是正数
  • 当 s = 1 时是负数
  • 对于数值 0 的符号位解释作为特殊情况处理
• 尾数（significand）M 是一个二进制小数，它的表示范围是 $1\sim 2-ϵ\text{（无穷小）}$
• 阶码（exponent）E 的作用是对浮点数加权，这个权重是 2 的 E 次幂

在单精度浮点格式（C 语言中的 float），s、exp、frac 字段分别为 1 位、k = 8 位和 n = 23 位，得到一个 32 位的表示。

在双精度浮点格式（C 语言中的 double），s、exp、frac 字段分别为 1 位、k = 11 位和 n = 52 位，得到一个 64 位的表示。

有效数字 M

• 前面说过，1 ≤ M < 2，也就是说，M 可以写成 1.xxx 的形式，其中 xxx 表示小数部分
• IEEE 754 规定，在计算机内部保存 M 时，默认这个数的第一位总是 1，因此 1 可以被舍去，只保存后面的 xxx 部分
  • 比如保存 1.01 的时候，只保存 01 ，等到读取的时候，再把第一位的 1 加上去，这样做的目的，是为了节省 1 位有效数字
• 以 32 位浮点数为例，留给 M 只有 23 位，将第一位的 1 舍去以后，相当于可以保存 24 位有效数字

C 语言中 float 和 double 表示的精度

• float 占用 32 位，其中 24 位用于存放尾数，所以 float 有 24 个二进制有效位位数

  • $10^7<2^{24}=16777216<10^8$
  • 所以 C 语言 float 的有效数字位是 $7$ 位
    • 注意是有效位数，不是小数点后的位数

  有时会不足 7 位，这是因为发生舍入导致的。

  有时又会超过 7 位，具体原因可以看：为什么说 32 位浮点数的精度是 7 位有效数

• double 占用 64 位，其中 53 位用于存放尾数，所以 double 有 53 个二进制有效位位数

  • $10^{15}<2^{53}=9007199254740992<10^{16}$
  • 所以 C 语言 double 的有效数字位是 $15$ 位

指数 E

E 为一个无符号整数：

• 这意味着，如果 E 为 8 位，它的取值范围为 $0\sim 255$；如果 E 为 11 位，它的取值范围为 $0\sim 2047$
• 科学计数法中的 E 是可以出现负数的，所以 IEEE 754 规定，存入内存时 E 的真实值必须再加上一个中间数
  • 对于 8 位的 E，这个中间数是 127
  • 对于 11 位的 E，这个中间数是 1023
• 比如，$2^{10}$ 的 E 是 10，所以保存成 32 位浮点数时，必须保存成 $10+127=137$，即 $10001001$

指数 E 从内存中取出还可以再分成三种情况：

E 不全为 0 或不全为 1：

这时，浮点数就采用下面的规则表示，即指数 E 的计算值减去 127（或 1023），得到真实值，再将有效数字 M 前加上第一位的 1。

比如：0.5 的二进制形式为 0.1，由于规定正数部分必须为 1，即将小数点右移 1 位，则为 $1.0\times 2^{-1}$，其阶码为 $-1+127=126$，表示为 $01111110$，而尾数 1.0 去掉整数部分为 0，补齐 0 到 23 位 $00000000000000000000000$，则其二进制表示形式为： $00111111000000000000000000000000$。

E 全为 0：

这时，浮点数的指数 E 等于 $1-127$（或者 $1-1023$），有效数字 M 不再加上第一位的 1，而是还原为 0.xxxxxx 的小数。这样做是为了表示 $\pm 0$，以及接近于 0 的很小的数字。

E 全为 1：

这时，如果有效数字 M 全为 0，表示 $\pm \infty$（正负取决于符号位 s）。如果有效数字 M 不全为 0，结果值被称为 NaN，即不是一个数（Not a Number）的缩写。