用Python进行数学建模（二）

一、微分方程模型

微分方程是描述系统的状态随时间和空间演化的数学工具。物理中许多涉及变力的运动学、动力学问题，如空气的阻力为速度函数的落体运动等问题，很多可以用微分方程求解。微分方程在化学、工程学、经济学和人口统计等领域也有广泛应用。

具体来说，微分方程是指含有未知函数及其导数的关系式。

微分方程的数学建模其实并不复杂，基本过程就是分析题目属于哪一类问题、可以选择什么微分方程模型，然后如何使用现有的微分方程模型建模。

1.微分方程的数值解法

微分方程的数值求解是先把时间和空间离散化，然后将微分化为差分，建立递推关系，然后反复进行迭代计算，得到任意时间和空间的值。

2.SciPy 求解常微分方程（组）

1.一阶常微分方程（组）模型

2.scipy.integrate.odeint() 函数

函数原型

参数解释
func:callable(y, t, …) or callable(t, y, …)
计算y在t点的导数。如果签名是可调用的(t, y，…)，那么参数tfirst必须设置为True。
y0:array
y的初始条件 (可以是vector).
t:array
要解出y的时间点序列。初值点应该是这个序列的第一个元素。这个序列必须是单调递增或单调递减的;允许重复值。
args:tuple, optional
向导数函数 func 传递参数。当导数函数 f ( y , t , p 1 , p 2 , . . ) f(y,t,p1,p2,…)f(y,t,p1,p2,…) 包括可变参数 p1,p2… 时，通过 args =(p1,p2,…) 可以将参数p1,p2… 传递给导数函数 func。

odeint 的主要返回值
y: array
数组，形状为 (len(t),len(y0)，给出时间序列 t 中每个时刻的 y 值。

3.Scipy 求解一阶常微分方程

1.scipy.integrate.odeint() 求解常微分方程初值问题的步骤

2.求微分方程的数值解

from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

def dy_dt(y, t):  # 定义函数 f(y,t)
    return np.sin(t**2)

y0 = [1]  # y0 = 1 也可以
t = np.arange(-10,10,0.01)  # (start,stop,step)
y = odeint(dy_dt, y0, t)  # 求解微分方程初值问题

# 绘图
plt.plot(t, y)
plt.title("scipy.integrate.odeint")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4.Scipy 求解一阶常微分方程组

1.求洛伦兹（Lorenz）方程的数值解

2.洛伦兹（Lorenz）方程问题的编程步骤

3.代码

from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# 导数函数, 求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W, t, p, r, b):
    x, y, z = W  # W=[x,y,z]
    dx_dt = p * (y - x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x * (r - z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x * y - b * z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt, dy_dt, dz_dt])


t = np.arange(0, 30, 0.01)  # 创建时间点 (start,stop,step)
paras = (10.0, 28.0, 3.0)  # 设置 Lorenz 方程中的参数 (p,r,b)

# 调用ode对lorenz进行求解, 用两个不同的初始值 W1、W2 分别求解
W1 = (0.0, 1.00, 0.0)  # 定义初值为 W1
track1 = odeint(lorenz, W1, t, args=(10.0, 28.0, 3.0))  # args 设置导数函数的参数
W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
fig = plt.figure()
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax)
ax.plot(track1[:, 0], track1[:, 1], track1[:, 2], color='magenta')  # 绘制轨迹 1
ax.plot(track2[:, 0], track2[:, 1], track2[:, 2], color='deepskyblue')  # 绘制轨迹 2
ax.set_title("Lorenz attractor by scipy.integrate.odeint")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

4.结果

5.Scipy 求解高阶常微分方程

高阶常微分方程，必须做变量替换，化为一阶微分方程组，再用 odeint 求数值解。
1.求二阶 RLC 振荡电路的数值解

2.二阶微分方程问题的编程步骤

3.代码

from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt


# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2 * a * v - w * w * u]
    return dY_dt


t = np.arange(0, 20, 0.01)  # 创建时间点 (start,stop,step)
# 设置导数函数中的参数 (a, w)
paras1 = (1, 0.6)  # 过阻尼：a^2 - w^2 > 0
paras2 = (1, 1)  # 临界阻尼：a^2 - w^2 = 0
paras3 = (0.3, 1)  # 欠阻尼：a^2 - w^2 < 0

# 调用ode对进行求解, 用两个不同的初始值 W1、W2 分别求解
Y0 = (1.0, 0.0)  # 定义初值为 Y0=[u0,v0]
Y1 = odeint(deriv, Y0, t, args=paras1)  # args 设置导数函数的参数
Y2 = odeint(deriv, Y0, t, args=paras2)  # args 设置导数函数的参数
Y3 = odeint(deriv, Y0, t, args=paras3)  # args 设置导数函数的参数

# 绘图
plt.plot(t, Y1[:, 0], 'r-', label='u1(t)')
plt.plot(t, Y2[:, 0], 'b-', label='u2(t)')
plt.plot(t, Y3[:, 0], 'g-', label='u3(t)')
plt.plot(t, Y1[:, 1], 'r:', label='v1(t)')
plt.plot(t, Y2[:, 1], 'b:', label='v2(t)')
plt.plot(t, Y3[:, 1], 'g:', label='v3(t)')
plt.axis([0, 20, -0.8, 1.2])
plt.legend(loc='best')
plt.title("Second ODE by scipy.integrate.odeint")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

4.结果

二、微分方程边值问题（BVP）

微分方程是指含有未知函数及其导数的关系式。

微分方程是描述系统的状态随时间和空间演化的数学工具。

微分方程分为初值问题和边值问题。初值问题是已知微分方程的初始条件，即自变量为零时的函数值，一般可以用欧拉法、龙哥库塔法来求解。边值问题则是已知微分方程的边界条件，即自变量在边界点时的函数值。

1.常微分方程边值问题的数学模型

2.SciPy 求解常微分方程边值问题

1.BVP 问题的标准形式

2.scipy.integrate.solve_bvp() 函数
可以求解一阶微分方程（组）的两点边值问题（第一类边界条件）。

solve_bvp 的主要参数：
func: callable fun(x, y, …) 　　导数函数 f ( y , x ) f(y,x)f(y,x) ， y 在 x 处的导数，以函数的形式表示。可以带有参数 p。
bc: callable bc(ya, yb, …) 　　边界条件，y 在两点边界的函数，以函数的形式表示。可以带有参数 p。
x: array：　　初始网格的序列，shape (m,)。必须是单调递增的实数序列，起止于两点边界值 xa，xb。
y: array：　　网格节点处函数值的初值，shape (n,m)，第 i 列对应于 x[i]。

solve_bvp 的主要返回值：
sol: PPoly 　　通过 PPoly （如三次连续样条函数）插值求出网格节点处的 y 值。
x: array 　　数组，形状为 (m,)，最终输出的网格节点。
y: array 　　二维数组，形状为 (n,m)，输出的网格节点处的 y 值。
yp: array 　　二维数组，形状为 (n,m)，输出的网格节点处的 y’ 值。

3.一阶常微分方程边值问题

1.标准化

2.编程步骤

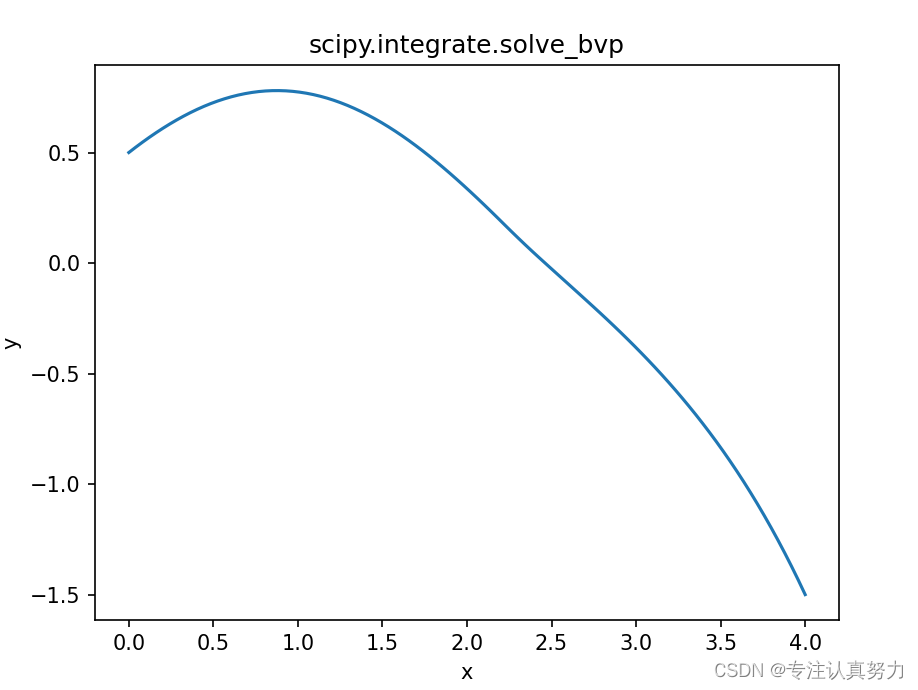
3.代码

from scipy.integrate import odeint, solve_bvp
import numpy as np
import matplotlib.pyplot as plt


# 1. 求解微分方程组边值问题，DEMO
# y'' + abs(y) = 0, y(0)=0.5, y(4)=-1.5

# 导数函数，计算导数 dY/dx
def dydx(x, y):
    dy0 = y[1]
    dy1 = -abs(y[0])
    return np.vstack((dy0, dy1))


# 计算 边界条件
def boundCond(ya, yb):
    fa = 0.5  # 边界条件 y(xa=0) = 0.5
    fb = -1.5  # 边界条件 y(xb=4) = -1.5
    return np.array([ya[0] - fa, yb[0] - fb])


xa, xb = 0, 4  # 边界点 (xa,xb)
# fa, fb = 0.5, -1.5  # 边界点的 y值
xini = np.linspace(xa, xb, 11)  # 确定 x 的初值
yini = np.zeros((2, xini.size))  # 确定 y 的初值
res = solve_bvp(dydx, boundCond, xini, yini)  # 求解 BVP

xSol = np.linspace(xa, xb, 100)  # 输出的网格节点
ySol = res.sol(xSol)[0]  # 网格节点处的 y 值

plt.plot(xSol, ySol, label='y')
plt.xlabel("x")
plt.ylabel("y")
plt.title("scipy.integrate.solve_bvp")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

4.执行结果

4.水滴横截面的形状

from scipy.integrate import odeint, solve_bvp
import numpy as np
import matplotlib.pyplot as plt


# 3. 求解微分方程边值问题，水滴的横截面
# 导数函数，计算 h=[h0,h1] 点的导数 dh/dx
def dhdx(x, h):
    # 计算 dh0/dx, dh1/dx 的值
    dh0 = h[1]  # 计算 dh0/dx
    dh1 = (h[0] - 1) * (1 + h[1] * h[1]) ** 1.5  # 计算 dh1/dx
    return np.vstack((dh0, dh1))


# 计算 边界条件
def boundCond(ha, hb):
    # ha = 0  # 边界条件：h0(x=-1) = 0
    # hb = 0  # 边界条件：h0(x=1) = 0
    return np.array([ha[0], hb[0]])


xa, xb = -1, 1  # 边界点 (xa=0, xb=1)
xini = np.linspace(xa, xb, 11)  # 设置 x 的初值
hini = np.zeros((2, xini.size))  # 设置 h 的初值

res = solve_bvp(dhdx, boundCond, xini, hini)  # 求解 BVP
# scipy.integrate.solve_bvp(fun, bc, x, y,..)
#   fun(x, y, ..), 导数函数 f(y,x)，y在 x 处的导数。
#   bc(ya, yb, ..), 边界条件，y 在两点边界的函数。
#   x: shape (m)，初始网格的序列，起止于两点边界值 xa，xb。
#   y: shape (n,m)，网格节点处函数值的初值，第 i 列对应于 x[i]。

xSol = np.linspace(xa, xb, 100)  # 输出的网格节点
hSol = res.sol(xSol)[0]  # 网格节点处的 h 值
plt.plot(xSol, hSol, label='h(x)')
plt.xlabel("x")
plt.ylabel("h(x)")
plt.axis([-1, 1, 0, 1])
plt.title("Cross section of water drop by BVP")
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

5.带有未知参数的微分方程边值问题

from scipy.integrate import odeint, solve_bvp
import numpy as np
import matplotlib.pyplot as plt


# 4. 求解微分方程组边值问题，Mathieu 方程
# y0' = y1, y1' = -(lam-2*q*cos(2x))y0)
# y0(0)=1, y1(0)=0, y1(pi)=0

# 导数函数，计算导数 dY/dx
def dydx(x, y, p):  # p 是待定参数
    lam = p[0]
    q = 10
    dy0 = y[1]
    dy1 = -(lam - 2 * q * np.cos(2 * x)) * y[0]
    return np.vstack((dy0, dy1))


# 计算 边界条件
def boundCond(ya, yb, p):
    lam = p[0]
    return np.array([ya[0] - 1, ya[0], yb[0]])


xa, xb = 0, np.pi  # 边界点 (xa,xb)
xini = np.linspace(xa, xb, 11)  # 确定 x 的初值
xSol = np.linspace(xa, xb, 100)  # 输出的网格节点

for k in range(5):
    A = 0.75 * k
    y0ini = np.cos(8 * xini)  # 设置 y0 的初值
    y1ini = -A * np.sin(8 * xini)  # 设置 y1 的初值
    yini = np.vstack((y0ini, y1ini))  # 确定 y=[y0,y1] 的初值
    res = solve_bvp(dydx, boundCond, xini, yini, p=[10])  # 求解 BVP
    y0 = res.sol(xSol)[0]  # 网格节点处的 y 值
    y1 = res.sol(xSol)[1]  # 网格节点处的 y 值
    plt.plot(xSol, y0, '--')
    plt.plot(xSol, y1, '-', label='A = {:.2f}'.format(A))

plt.xlabel("hbu")
plt.ylabel("y")
plt.title("Characteristic function of Mathieu equation")
plt.axis([0, np.pi, -5, 5])
plt.legend(loc='best')
plt.text(2, -4, "hao-hbu", color='whitesmoke')
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

三、非线性规划

1.非线性规划问题的描述

2.scipy.optimize.brent() 求解单变量无约束优化问题

非线性规划最简单的形式是一维搜索，一维搜索的常用方法是函数逼近法和区间收缩法。

brent() 函数是 SciPy.optimize 模块中求解单变量无约束优化问题最小值的首选方法。这是牛顿法和二分法的混合方法，既能保证稳定性又能快速收敛。

optimize.brent() 的主要参数：
func: callable f(x,args) 　　目标函数 f ( x ) f(x)f(x)，以函数形式表示，可以通过 *args 传递参数
args: tuple　　可选项，以 f(x,*args) 的形式将可变参数 p 传递给目标函数 f ( x , p ) f(x,p)f(x,p) 。
brack: tuple　　可选项，搜索算法的开始区间（不是指 x 的上下限）

optimize.brent() 的主要返回值：
xmin: 　　返回函数达到最小值时的 x（注意是局部最优，不一定是全局最优）。
fval: 　　返回函数的最优值（默认不返回，仅当 full_output 为 1 时返回）。

optimize.brent() 的使用例程：

import numpy as np
from scipy.optimize import brent
import matplotlib.pyplot as plt


# 1. Demo1：单变量无约束优化问题(Scipy.optimize.brent)
def objf(x):  # 目标函数
    fx = x ** 2 - 8 * np.sin(2 * x + np.pi)
    return fx


xIni = -5.0
xOpt = brent(objf, brack=(xIni, 2))
print("xIni={:.4f}\tfxIni={:.4f}".format(xIni, objf(xIni)))
print("xOpt={:.4f}\tfxOpt={:.4f}".format(xOpt, objf(xOpt)))

x = np.linspace(-10, 10, 500)
plt.plot(x, objf(x))
plt.xlabel("x")
plt.ylabel("objf(x)")
plt.text(xIni, objf(xIni), "Initial")
plt.text(xOpt, objf(xOpt), "Best")
plt.scatter(xIni, objf(xIni))
plt.scatter(xOpt, objf(xOpt))
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

运行结果：

3.scipy.optimize.fmin() 求解多变量无约束优化问题

fmin() 函数是 SciPy.optimize 模块中求解多变量无约束优化问题（最小值）的首选方法，采用下山单纯性方法。下山单纯性方法又称 Nelder-Mead 法，只使用目标函数值，不需要导数或二阶导数值，是最重要的多维无约束优化问题数值方法之一。

from scipy.optimize import brent, fmin, minimize
import numpy as np
​
# 2. Demo2：多变量无约束优化问题(Scipy.optimize.brent)
# Rosenbrock 测试函数
def objf2(x):  # Rosenbrock benchmark function
    fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
    return fx
​
xIni = np.array([-2, -2])
xOpt = fmin(objf2, xIni)
print("xIni={:.4f},{:.4f}\tfxIni={:.4f}".format(xIni[0],xIni[1],objf2(xIni)))
print("xOpt={:.4f},{:.4f}\tfxOpt={:.4f}".format(xOpt[0],xOpt[1],objf2(xOpt)))
1
2
3
4
5
6
7
8
9
10
11
12
13

4.scipy.optimize.minimize() 求解非线性规划问题

minimize() 函数是 SciPy.optimize 模块中求解多变量优化问题的通用方法，可以调用多种算法，支持约束优化和无约束优化。

import numpy as np
from scipy.optimize import minimize


# 定义目标函数
def objf3(x):  # Rosenbrock 测试函数
    fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
    return fx


# 定义边界约束（优化变量的上下限）
b0 = (0.0, None)  # 0.0 <= x[0] <= Inf
b1 = (0.0, 10.0)  # 0.0 <= x[1] <= 10.0
b2 = (-5.0, 100.)  # -5.0 <= x[2] <= 100.0
bnds = (b0, b1, b2)  # 边界约束

# 优化计算
xIni = np.array([1., 2., 3.])
resRosen = minimize(objf3, xIni, method='SLSQP', bounds=bnds)
xOpt = resRosen.x

print("xOpt = {:.4f}, {:.4f}, {:.4f}".format(xOpt[0], xOpt[1], xOpt[2]))
print("min f(x) = {:.4f}".format(objf3(xOpt)))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

5.约束非线性规划问题实例

import numpy as np
from scipy.optimize import minimize


def objF4(x):  # 定义目标函数
    a, b, c, d = 1, 2, 3, 8
    fx = a * x[0] ** 2 + b * x[1] ** 2 + c * x[2] ** 2 + d
    return fx


# 定义约束条件函数
def constraint1(x):  # 不等式约束 f(x)>=0
    return x[0] ** 2 - x[1] + x[2] ** 2


def constraint2(x):  # 不等式约束 转换为标准形式
    return -(x[0] + x[1] ** 2 + x[2] ** 3 - 20)


def constraint3(x):  # 等式约束
    return -x[0] - x[1] ** 2 + 2


def constraint4(x):  # 等式约束
    return x[1] + 2 * x[2] ** 2 - 3


# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)

# 定义约束条件
con1 = {'type': 'ineq', 'fun': constraint1}
con2 = {'type': 'ineq', 'fun': constraint2}
con3 = {'type': 'eq', 'fun': constraint3}
con4 = {'type': 'eq', 'fun': constraint4}
cons = ([con1, con2, con3, con4])  # 3个约束条件

# 求解优化问题
x0 = np.array([1., 2., 3.])  # 定义搜索的初值
res = minimize(objF4, x0, method='SLSQP', bounds=bnds, constraints=cons)

print("Optimization problem (res):\t{}".format(res.message))  # 优化是否成功
print("xOpt = {}".format(res.x))  # 自变量的优化值
print("min f(x) = {:.4f}".format(res.fun))  # 目标函数的优化值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46