【基础教程】Matlab创建三维箱线图

主要介绍箱线图（Box-plot）和利用Matlab绘制箱线图。

1、箱线图介绍

统计指标一般包括：四分位数、均值、中位数、众数、方差、标准差等，箱线图作为一种数据统计的方法，内容包括：最小值，第一分位，中位数，第三分位数，最大值。

箱线图于1977年由美国著名统计学家约翰·图基（John Tukey）发明，能够明确的展示离群点的信息，同时能够让我们了解数据是否对称，数据如何分组、数据的峰度。

箱线图（Box-plot）是一种用于显示一组数据分散情况的统计图，多用于多组数据的比较，相对于直方图，既可以节省空间，还可以展示更多信息（如均值、四分位数等）。

箱线图包含数学统计量，能够分析不同类别数据各层次水平差异，还可以揭示数据间离散程度、异常值、分布差异等。

箱线图内容详细介绍：

【注】图片来自你似乎来到了没有知识存在的荒原 - 知乎

四分位数：
一组数据按照从小到大顺序排列后，把该组数据四等分的数，称为四分位数。第一四分位数 (Q1)、第二四分位数 (Q2，也叫“中位数”)和第三四分位数 (Q3)分别等于该样本中所有数值由小到大排列后第25%、第50%和第75%的数字。第三四分位数与第一四分位数的差距又称四分位距（interquartile range, IQR）。

（1）第一个四分位数Q1：也称作25th百分位数，表示最小数（不是“最小值”）和数据集的中位数之间的中间数。

（2）第二四分位数Q2：也称作中位数Median/50th百分位数，表示数据集的中间值。

（3）第三四分位数Q3：也称作75th百分位数，表示数据集的中位数和最大值之间的中间值（不是“最大值”）。

（4）四分位间距IQR：第25至第75个百分点的距离。

（5）离群值：Outliers

（6）最大值max、最小值min

利用正态分布的箱线图，可以帮助理解箱线图：

【注】图片来自你似乎来到了没有知识存在的荒原 - 知乎

2 完整代码

function boxPlot3D(xx,g1,g2,quantDistribution)
%function boxPlot3D(xx,g1,g2,quantDistribution)
%--------------------------------------------------------------------------
% boxPlot3D(x) creates a three dimensional box plot of the data in x. If x
% is 3D a matrix, boxPlot3D creates one box for each column. Example,
% create a 3D matrix with normal distributions with different means:
%
% xx=randn(50,2,4)+repmat((permute([0 1 2 -2;1 2 3 4],[3 1 2])),[50,1,1]);
% boxPlot3D(xx)
%
% boxPlot3D(x,g1,g2) groups the data of x, with the grouping variables of
% g1, and g2. Example, create a 1D Matrix with different values and the
% corresponding grouping parameters:
%
% xx=randn(500,1)+linspace(0,5,500)';
% g1= [0.1*ones(250,1);0.2*ones(250,1)];
% g2= [3*ones(150,1);4*ones(150,1);5*ones(200,1)];
% boxPlot3D(xx,g1,g2)
%
% boxPlot3D(x,[],[],quantDistribution) allows the selection of the
% quantiles to select, e.g. [0 0.25 0.5 0.75 1]
%    [0 0.25 0.5 0.75 1] (default)  creates a box between 0.25 and 0.75
%                         with a line in 0.5 and two planes at 0 and 1
%                         connected with a dashed line. These values can be
%                         changed.
%    [ 0 1]               creates a box within the extremes of the values
%                          selected. These values can be changed, e.g.
%                          [0.25 0.75]
%    [ 0.25 0.5 0.75]     creates a box and a line, same as the option with
%                         5 values, but will not draw the planes with the
%                         dashed line.
% The colours of the boxes can be changed in the code.
%--------------------------------------------------------------------------
%
%

if nargin <1
    
else
        figure
        hold on;
    if ~exist('quantDistribution','var')
        % Calculate the positions of the edges of the boxplot, and the
        % quantiles at 25,50 75%
        quantDistribution = [0 0.25  0.50  0.75 1 ];
    end
    if ~exist('g1','var')
        % Only one parameter received, the data is in a 3D Matrix with one
        % column per group.
        [rows,columns,levels] = size( xx);
        for counterCols = 1:columns
            for counterLevs = 1:levels
                % Select columns, extract positions, and call display
                % The column is directly extracted from the matrix
                currentColumn = xx(:,counterCols,counterLevs);
                % The positions correspond to the extreme, median and 25%/75%
                % positions of the distribution, these are obtained with
                % quantile
                currentPositions = quantile(currentColumn,quantDistribution);
                display3Dbox(counterCols,counterLevs,currentPositions);
            end
        end
    else
        % Three arguments, the data and two grouping parameters
        % all should be the same size. First, detect the unique cases of
        % each of the grouping parameters
        cases_g1=unique(g1);
        cases_g2=unique(g2);
        % Count how many cases there are for each dimension
        num_g1 = numel(cases_g1);
        num_g2 = numel(cases_g2);
        % The separation may vary and not necessarily be 0,1,2,3...
        width_g1 = min(diff(cases_g1));
        width_g2 = min(diff(cases_g2));
        
        
        for counterCols = 1:num_g1
            current_g1 = cases_g1(counterCols);
            address_g1   = (g1==current_g1);
            for counterLevs = 1:num_g2
                current_g2 = cases_g2(counterLevs);
                address_g2 = (g2==current_g2);
                % Select columns, extract positions, and call display
                % The column is directly extracted from the matrix
                currentColumn = xx((address_g1)&(address_g2));
                % The positions correspond to the extreme, median and 25%/75%
                % positions of the distribution, these are obtained with
                % quantile
                currentPositions = quantile(currentColumn,quantDistribution);
                % Call the display with the extra parameters for width
                display3Dbox(current_g1,current_g2,currentPositions,width_g1,width_g2);
            end
        end
        
        
    end
    view(3)
    rotate3d on
    axis tight
    grid on
    
end

end

function display3Dbox(counterCols,counterLevs,currentPositions,width_g1,width_g2)

if ~exist('width_g1','var')
    width_g1 = 1;
end
if ~exist('width_g2','var')
    width_g2 = 1;
end
if ~exist('colourFace','var')
    colourFace='red';
end
if ~exist('colourFace2','var')
    colourFace2='cyan';
end
lenZStats=length(currentPositions);

% to avoid overlap between boxes, use only 35% to each dimension
x=width_g1 * 0.35*[-1 1 1 -1 -1 1 1 -1]';
y=width_g2 * 0.35*[-1 -1 1 1 -1 -1 1 1]';
% This are the parameters to create the boxes and faces
z=[1 1 1 1]';
face_Mat=[1 2 6 5;2 3 7 6;3 4 8 7;4 1 5 8;4 1 5 8;1 2 3 4; 5 6 7 8];

switch lenZStats
    case 2
        %----- a single box with extremes (.25 .75 / 0 1) to be plotted
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(1)*z;currentPositions(2)*z]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace,'edgecolor','black','linewidth',1);
        
    case 3
        %----- a central box with median (0.25 0.5 0.75)
        delta=0.05*(currentPositions(3)-currentPositions(1));
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(1)*z;currentPositions(2)*z-delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace,'edgecolor','black','linewidth',1);
        
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(2)*z-delta/2;currentPositions(2)*z+delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace2,'edgecolor','black','linewidth',1);
        
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(2)*z+delta/2;currentPositions(3)*z-delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace,'edgecolor','black','linewidth',1);
        
    case 5
        %----- central box with extemes (0 0.25 0.5 0.75 1)
        delta=0.05*(currentPositions(3)-currentPositions(1));
        colourFace3=0.5*[1 1 1];
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(2)*z;currentPositions(3)*z-delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace,'edgecolor','black','linewidth',1);
        
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(3)*z-delta/2;currentPositions(3)*z+delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace2,'edgecolor','black','linewidth',1);
        
        vert_Mat=[counterCols+x counterLevs+y [currentPositions(3)*z+delta/2;currentPositions(4)*z-delta/2]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace,'edgecolor','black','linewidth',1);
        
        vert_Mat=[counterCols+x*(0.5) counterLevs+y*(0.5) [currentPositions(1)*z;currentPositions(1)*z]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace3,'edgecolor','black','linewidth',0.5);
        
        vert_Mat=[counterCols+x*(0.5) counterLevs+y*(0.5) [currentPositions(5)*z;currentPositions(5)*z]];
        patch('Vertices',vert_Mat,'Faces',face_Mat,'facecolor',colourFace3,'edgecolor','black','linewidth',0.5);
        line([counterCols counterCols],[counterLevs counterLevs],[currentPositions(1) currentPositions(2)],'linewidth',0.5,'color','k','marker','.','linestyle','--')
        line([counterCols counterCols],[counterLevs counterLevs],[currentPositions(4) currentPositions(5)],'linewidth',0.5,'color','k','marker','.','linestyle','--')
        
end

end
%delta=0.04;

%alpha(0.5);

%grid on;axis tight;rotate3d on;view(3)
 

3 运行结果

 

 

 

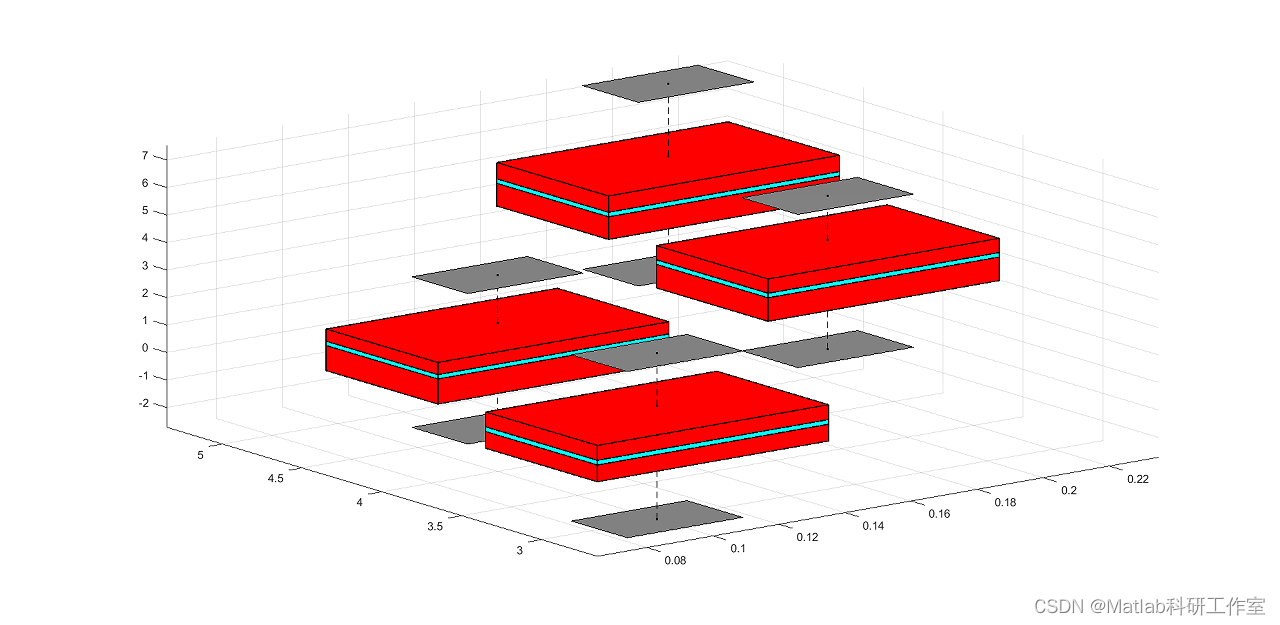
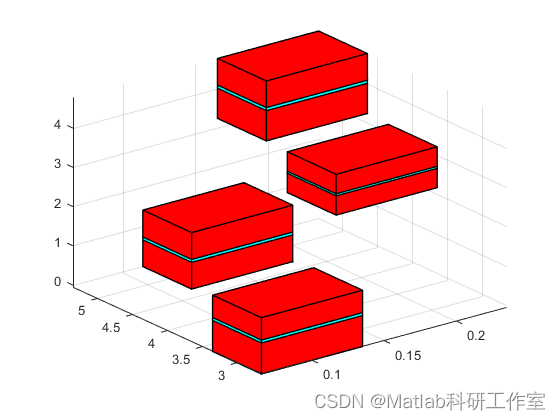
4 参考文献

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机、雷达通信、无线传感器等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。