排序算法大总结

1. 排序的相关概念

1. 稳定性： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
2. 内部排序：数据元素全部放在内存中的排序。
3. 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

为什么要有稳定性？
在例如淘宝的一些网购平台选购商品时，我们有时候会同时选择销量和价格的排序，这时就需要具有稳定性的排序了。

2. 排序的分类

3. 常见排序的实现

3.1 冒泡排序

3.1.1 原理

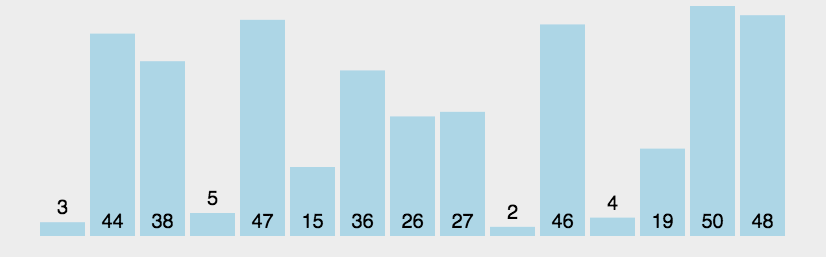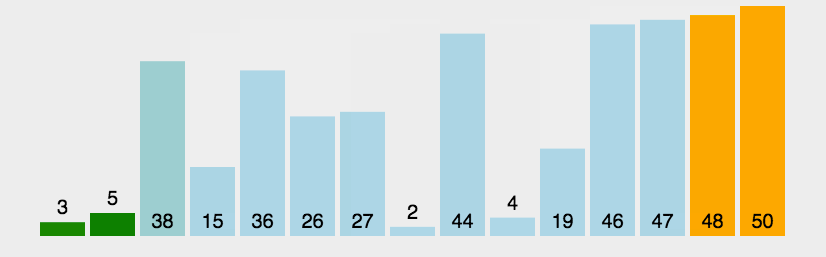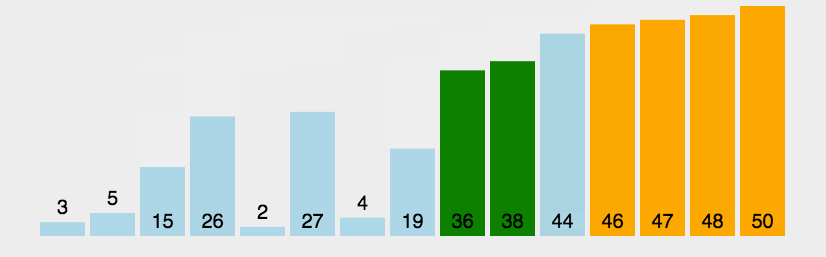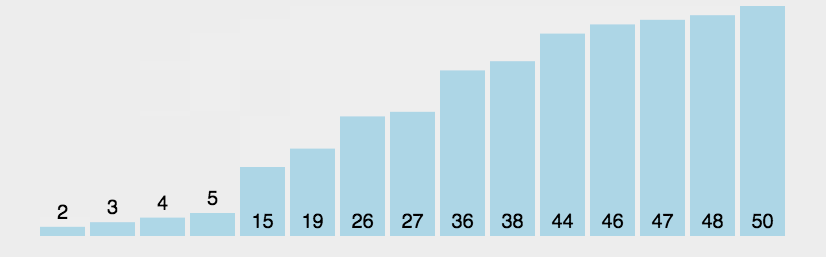
冒泡排序每趟能将一个数据排到正确位置，因此只需要排n-1趟。

3.1.2 代码实现

void Swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void BubbleSort(int a[], int sz)
{
    for (int i = 0; i < sz - 1; i++)
    {
        int flag = 0;
        for (int j = 0; j < sz - i - 1; j++)
        {
            if (a[j] > a[j + 1])
            {
                Swap(a + j, a + j + 1);
                flag = 1;
            }
        }
        if (flag == 0)
            break;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3.2 选择排序

3.2.1 原理

3.2.2 代码实现

void Swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}
void SelectSort(int arr[], int sz)
{
    int begin = 0;
    int end = sz - 1;
    while (begin < end)
    {
        int max = begin;
        int min = begin;
        for (int i = begin + 1; i <= end; i++)
        {
            if (arr[i] > arr[max])
            {
                max = i;
            }
            else if (arr[i] < arr[min])
            {
                min = i;
            }
        }
        Swap(arr + min, arr + begin);
        if (max == begin)
        {
            Swap(arr + min, arr + end);
        }
        else
        {
            Swap(arr + max, arr + end);
        }
        end--;
        begin++;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

3.3 直接插入排序

3.3.1 原理

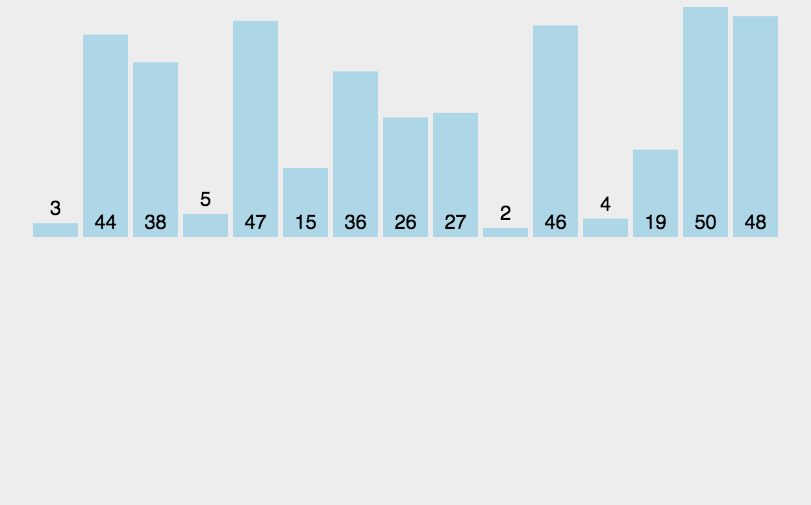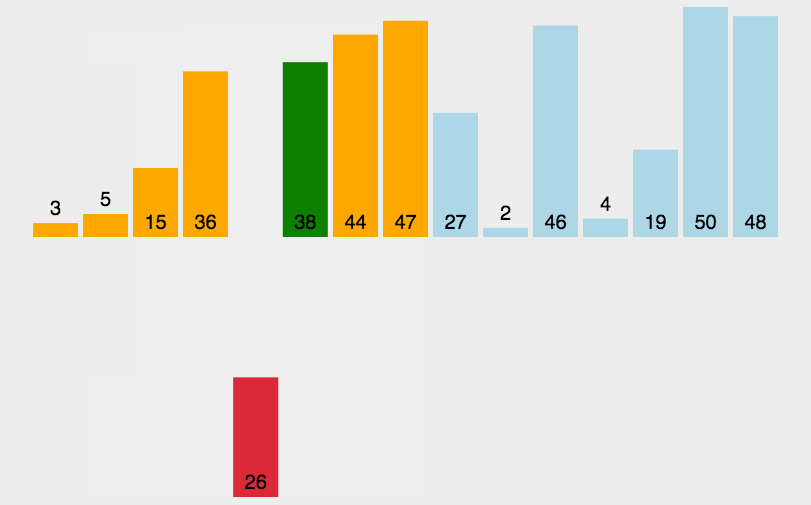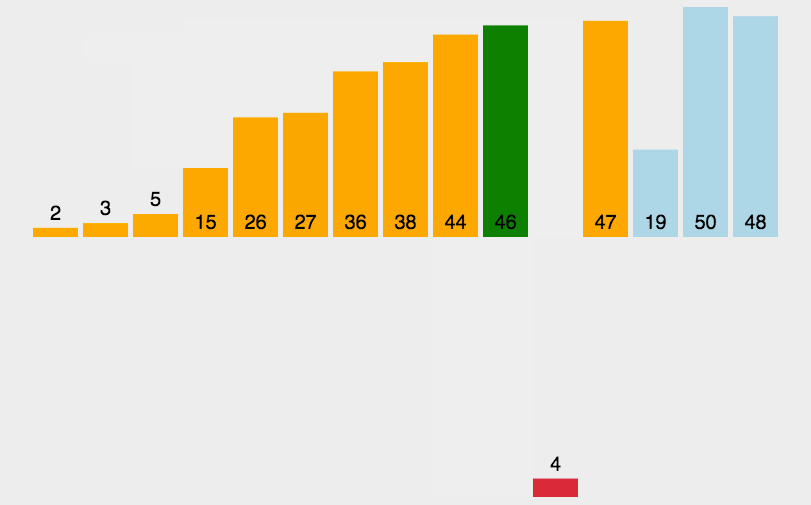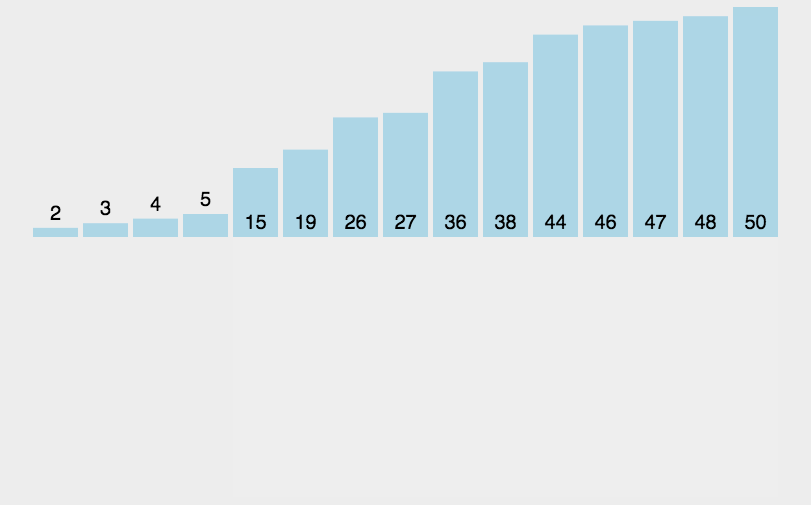
3.3.2 代码实现

void Swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}
void InsertSort(int arr[], int sz)
{
    for (int i = 1; i < sz; i++)
    {
        int tmp = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > tmp)
        {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = tmp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.4 希尔排序

3.4.1 原理

希尔排序是基于插入排序算法的一种排序，该排序设置了一个gap值，gap为一趟插入排序中两个值之间的间隔大小，每一趟插入排序完成后，gap变为原来的二分之一或者三分之一，直到gap变为1，再经历一次插入排序后，就可以完成排序~

3.4.2 代码实现

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap>1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int tmp = a[i + gap];
			int j = i;
			while ( j >= 0&& a[j] > tmp)
			{
				a[j + gap] = a[j];
				j -= gap;
			}
			a[j + gap] = tmp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.5 堆排序

3.5.1 原理

堆是一种具有特殊性质的二叉树，一般用数组实现。

堆分为大根堆和小根堆，大根堆是父亲节点要比两个子节点的值大，小根堆相反。
进行堆排序时，将大根堆或者小根堆的根节点与最后一个节点交换，并重新将根节点进行向下调整。

3.5.2 代码实现

代码实现一般分为两步：

1. 将数组调整为大根堆或者小根堆，如果想排升序则调为大根堆，想排降序则调为小根堆。
2. 将根节点与最后一个节点交换，并对根节点进行向下调整。

在第一步中，将数组调为堆结构有两种方法：

• 从数组第一个数据开始，向上调整建堆
• 从数组(sz-1)/2的数据开始，向下调整建堆：：把数组看作二叉树，则（sz-1）/2即是二叉树倒数第二层的最后一个节点。

两个方案哪个更好呢？
答：方案二更好
因为二叉树的最后一层的节点树几乎占据整个树节点的二分之一，而方案二将最后一层节点的调整省去了，即省去了大量的时间。

void AdjustDown(int* a, int parent, int sz)
{
	int son = parent * 2 + 1;
	if (son + 1 < sz && a[son] < a[son+1])
	{
		son++;
	}
	while (son < sz)
	{
		if (son + 1 < sz && a[son] < a[son + 1])
		{
			son++;
		}
		if (a[parent] < a[son])
		{
			Swap(&a[parent], &a[son]);
			parent = son;
			son = son * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int sz)
{
	for (int i = (sz - 2) / 2; i >= 0; i--)
	{
		AdjustDown(a, i, sz);
	}
	int j = sz - 1;
	while (j)
	{
		Swap(&a[0], &a[j]);
		AdjustDown(a, 0, j);
		j--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

3.6 快速排序

3.6.1 原理

3.6.1.1 hoare法

创建两个变量L和R，R先出发，遇到小于key值的数据或者遇到L停下，L再出发，遇到大于key值的数据或者遇到R停下，交换L和R的的值。

3.6.1.2 挖坑法

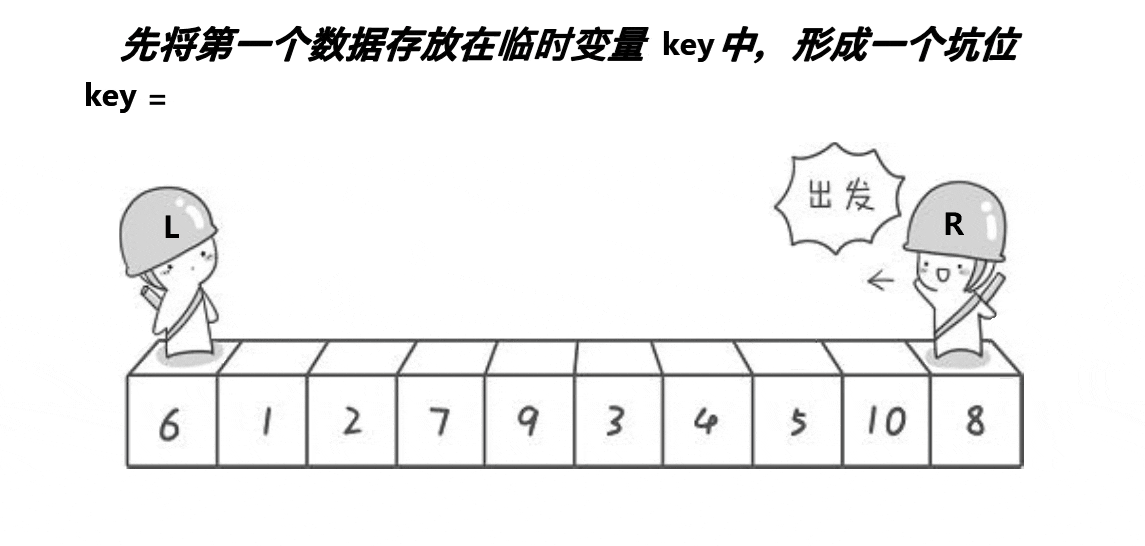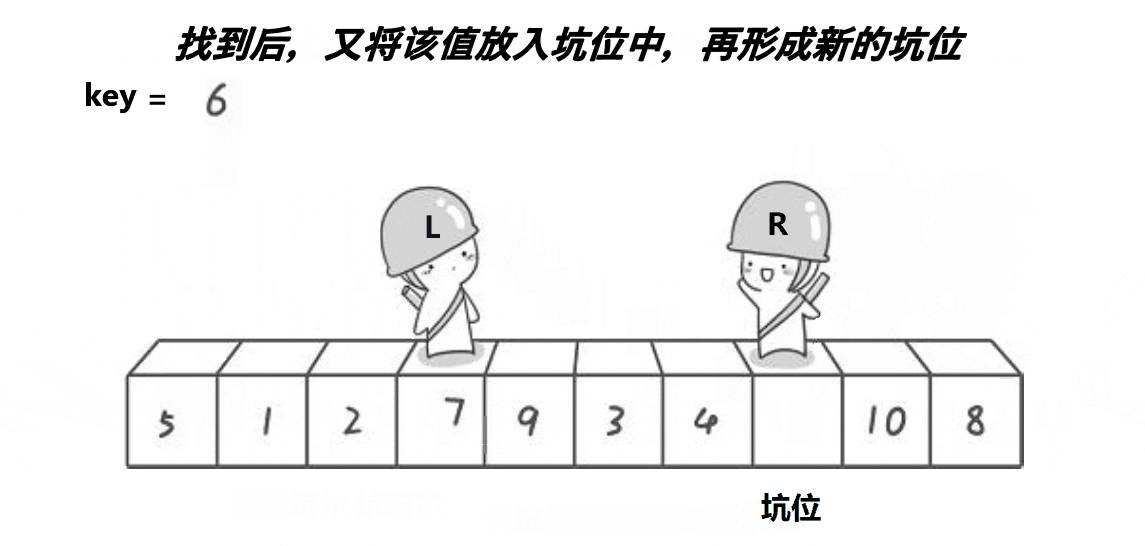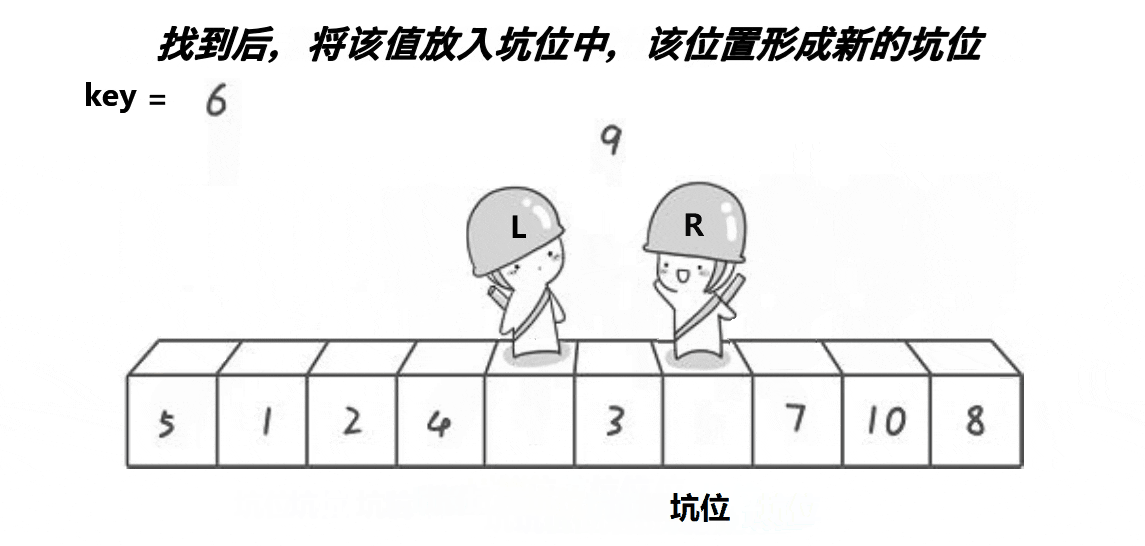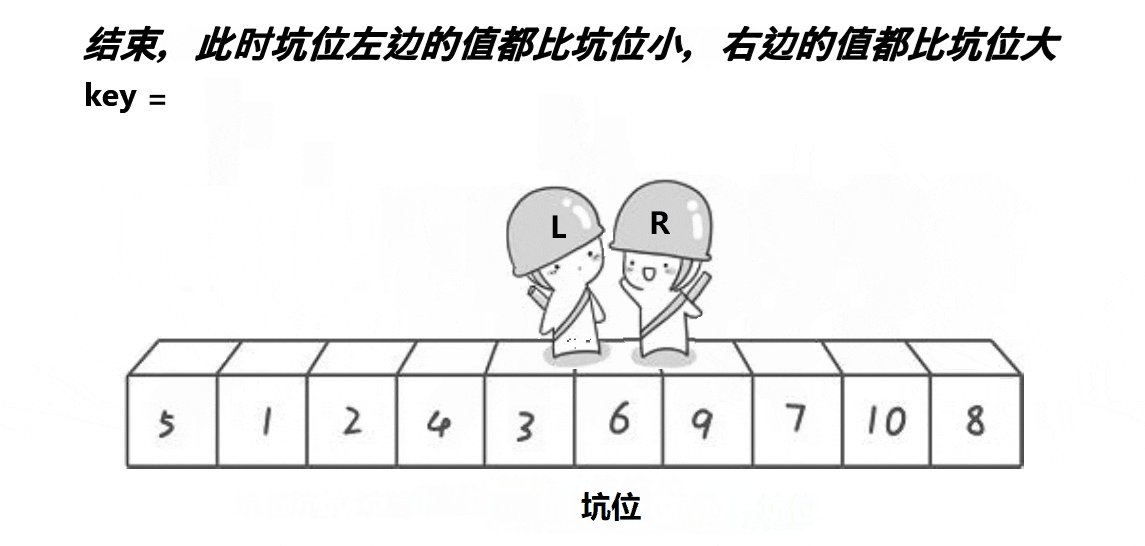
3.6.1.3 前后指针法

3.6.2 代码实现

3.6.2.1 hoare法

int PartSort1(int* a, int left, int right)
{
    int mid = SearchMid(a, left, right);
    Swap(&a[left], &a[mid]);
	int key = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[key], &a[right]);
	return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.6.2.2 挖坑法

int PartSort2(int* a, int left, int right)
{
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.6.2.3 双指针法

int PartSort3(int* a, int left, int right)
{
	int key = left;
	int prev = left;
	int cur = left+1;
	while (cur <= right)
	{
		if (a[cur] < a[key] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		else
		{
			cur++;
		}
	}
	Swap(&a[key], &a[prev]);
	return prev;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.6.2.4 递归实现快排

int SearchMid(int* a,int left,int right)
{
	int mid = left + (right - left) / 2;
	if (a[left] > a[right])
	{
		if (a[right] > a[mid])
		{
			return right;
		}
		else if (left < mid)
		{
			return left;
		}
		else
		{
			return mid;
		}
	}
	else
	{
		if (a[right] < a[mid])
		{
			return right;
		}
		else if (a[mid] > a[left])
		{
			return mid;
		}
		else
		{
			return left;
		}
	}
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int mid = SearchMid(a, left, right);
	Swap(&a[left], &a[mid]);
	int key = PartSort(a, left, right);
	QuickSort(a, left, key - 1);
	QuickSort(a, key + 1, right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

3.6.2.5 非递归实现快排

void QuickSortNonR(int* a, int left, int right)
{
	Stack s;
	StackInit(&s);
	StackPush(&s, left);
	StackPush(&s, right);
	while (!StackEmpty(&s))
	{
		right = StackTop(&s);
		StackPop(&s);
		left = StackTop(&s);
		StackPop(&s);
		if (right > left)
		{
			int key = PartSort1(a, left, right);
			StackPush(&s, key+1);
			StackPush(&s, right);
			StackPush(&s, left);
			StackPush(&s, key-1);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.7 归并排序

3.7.1 原理

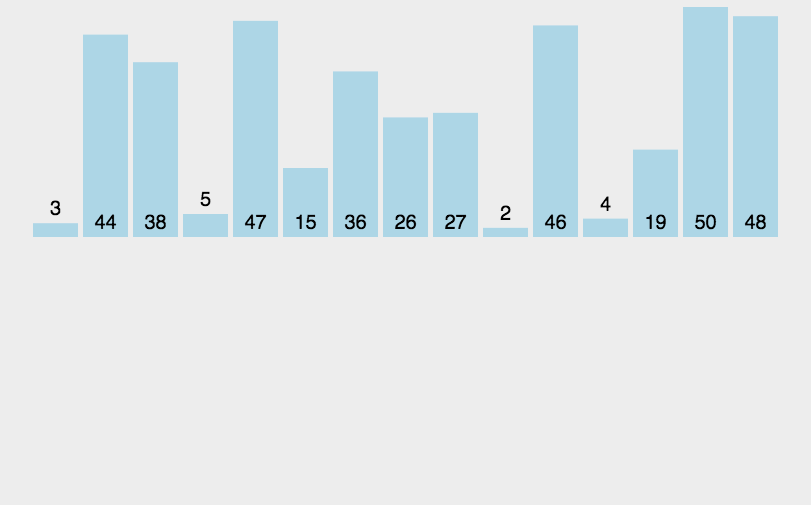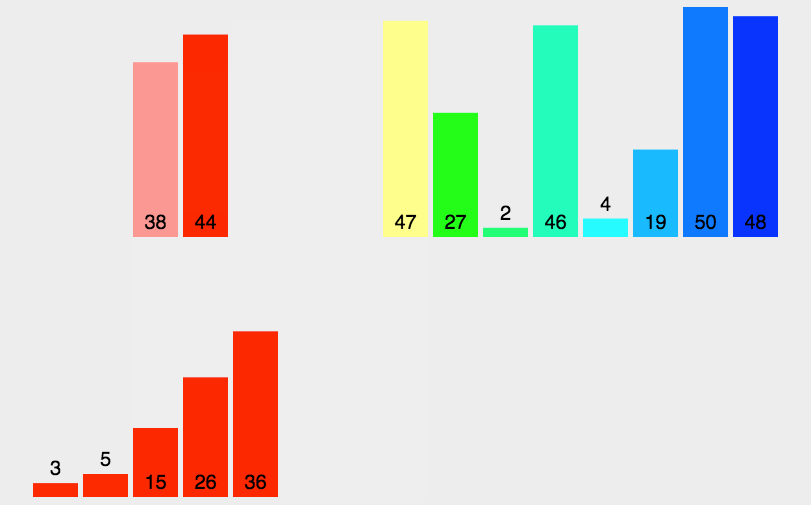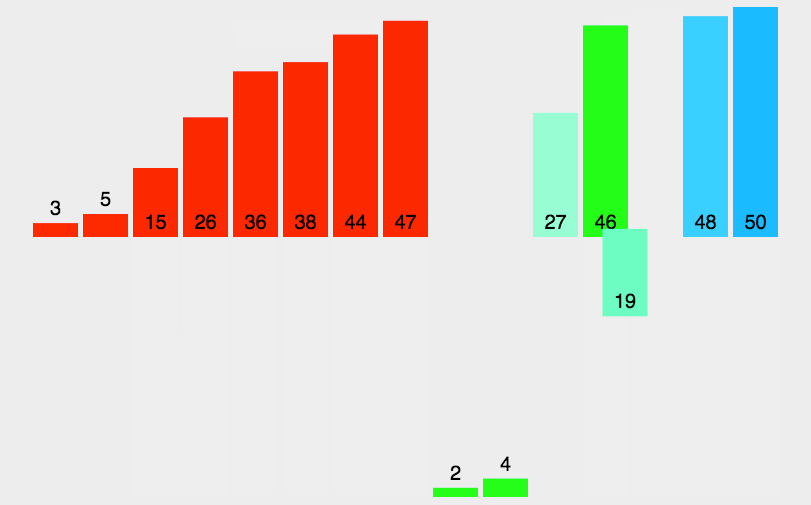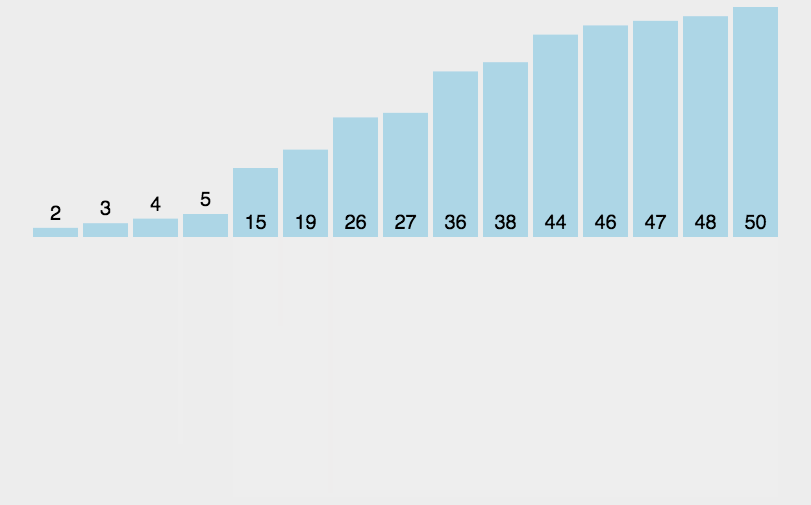
3.7.2 代码实现

3.7.2.1 递归实现归并

void _MergeSort(int a[], int tmp[], int begin, int end)
{
    if (begin >= end)
        return;
    int mid = begin + (end - begin) / 2;
    _MergeSort(a, tmp, begin, mid);
    _MergeSort(a, tmp, mid+1, end);
    int begin1 = begin, end1 = mid;
    int begin2 = mid + 1, end2 = end;
    int i = begin;
    while (begin1 <= end1 && begin2 <= end2)
    {
        if (a[begin1] <= a[begin2])
        {
            tmp[i++] = a[begin1++];
        }
        else
        {
            tmp[i++] = a[begin2++];
        }
    }
    while (begin1 <= end1)
    {
        tmp[i++] = a[begin1++];
    }
    while (begin2 <= end2)
    {
        tmp[i++] = a[begin2++];
    }
    memcpy(a+begin,tmp+begin,(end-begin+1)*sizeof(int));
}
void MergeSort(int a[], int sz)
{
    if (sz == 1)
        return;
    int* tmp = (int*)malloc(sizeof(int) * sz);
    if (tmp == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    _MergeSort(a,tmp,0,sz-1);
    free(tmp);
    tmp = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

3.7.2.2 非递归实现归并

void MergeSortNonR(int a[], int sz)
{
    int* tmp = (int*)malloc(sizeof(int)*sz);
    if(tmp == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    int gap = 1;
    while(gap <= sz)
    {
        int k = 0;
        for(int t = 0; t < sz; t += 2*gap)
        {
            int begin1 = t, end1 = t+gap-1;
            int begin2 = t+gap,end2 = t+gap*2-1;
            if(end1 >= sz-1)
            {
                break;
            }
            if(end2 >= sz)
            {
                end2 = sz-1;
            }
            int i = begin1;
            int j = begin2;
            while (i <= end1 && j <= end2)
            {
                if (a[i] <= a[j])
                {
                    tmp[k++] = a[i++];
                }
                else
                {
                    tmp[k++] = a[j++];
                }
            }
            while (i <= end1)
            {
                tmp[k++] = a[i++];
            }
            while (j <= end2)
            {
                tmp[k++] = a[j++];
            }
        }
        k--;
        while (k >= 0)
        {
            a[k] = tmp[k];
            k--;
        }
        gap *= 2;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

3.8 基数排序

代码实现

#define RADIX 10
#define K 3
int GetKey(int num, int k)
{
	while (k > 0)
	{
		num /= 10;
		k--;
	}
	return num % 10;
}

void RadixSort(int arr[],int sz)
{
	Queue q[RADIX];
	for (int i = 0; i < RADIX; i++)
	{
		QueueInit(q+i);
	}
	for (int i = 0; i < K; i++)
	{
		for (int j = 0; j < sz; j++)
		{
			int num = GetKey(arr[j], i);
			QueuePush(&q[num], arr[j]);
		}
		int k = 0;
		for (int j = 0; j < RADIX; j++)
		{
			while (!QueueEmpty(q + j))
			{
				arr[k++] = QueueFront(q + j);
				QueuePop(q + j);
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

3.9 计数排序

代码实现

void CountSort(int arr[], int sz)
{
	int min = arr[0];
	int max = arr[0];
	for (int i = 1; i < sz; i++)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
		else if (arr[i] < min)
		{
			min = arr[i];
		}
	}
	int* tmp = (int*)calloc(max-min+1, sizeof(int));
	if (tmp == NULL)
	{
		perror("calloc fail");
		exit(-1);
	}
	for (int i = 0; i < sz; i++)
	{
		tmp[arr[i] - min]++;
	}
	int k = 0;
	for (int i = 0; i < max - min + 1; i++)
	{
		while (tmp[i])
		{
			arr[k++] = i + min;
			tmp[i]--;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

3.10 睡眠排序和猴子排序

两个比较有意思的排序~

1. 睡眠排序是将数据的值设置为其睡眠时间的长度，时间到了就会苏醒，然后可以根据苏醒的先后来自动排序。
2. 猴子排序是将数据进行随机打乱，也就是如果运气好，一次打乱就能变为有序数据。所以也被称为欧皇排序。

4. 常见排序算法总结