基于Look-Ahead技术的机器人速度控制策略

基于Look-Ahead技术的机器人速度控制策略

1 背景介绍

机器人导航模块主要由全局规划器与局部规划器组成，其中全局路径规划器计算出一条能避开障碍物的路径，局部路径规划器根据全局规划器计算出的路径进一步对机器人的运行速度进行规划。
TEB（Time Elastic Band）算法将速度规划问题描述成一个多目标优化问题。即将最小化轨迹执行时间、与障碍物保持一定距离并遵守运动动力学约束等目标进行优化。因为优化的大多数目标都是局部的，只与机器人的某几个连续的状态有关，所以该问题为对稀疏模型的优化。
TEB算法对车辆前方的一段轨迹进行优化，具有很强的前瞻性，当前方突然出现障碍物时能及时刹车，具有良好的动态避障效果。然而TEB算法的计算复杂度很高，占用过多的CPU资源。另外TEB算法通过两状态之间的距离和角度差及时间差来计算该控制周期内的速度和角速度，使得在控制过程中速度和角度波动较大。
Look-Ahead 技术又称为速度前瞻控制技术。通过对路径段之间速度衔接及段内速度处理对速度进行规划，其优势在于其计算复杂度很低，而且规划出的速度连续性好，使得车辆在运行过程中表现得更加平稳。

2 速度前瞻技术

2.1 简介

速度控制是运动控制的重要内容。运动控制卡提供段内直线型或S型减速控制功能，导航时只需对每一段赋以进给速度，运动控制卡自动完成加减速处理。运动控制卡可以根据当前加工段和下一段之间夹角的大小进行段间加减速控制，夹角越大，降速越多，衔接点处的速度就越低。这些功能可以满足低速低负载运动控制场合对速度控制的要求。
导航给出的轨迹一般由大量的线段连接组成，当遇到轨迹急转弯等情况时，需要降到很低的速度。若只用运动控制卡提供的功能在相邻两段间进行加减速控制，由于线段很短，将产生巨大的加速度冲击。速度前瞻控制算法，是数控加工领域中的一种新的速度控制方法。它可以提前发现轨迹突变，从而按照安全的加速度提前减速。速度前瞻控制的两个关键问题是减速特征识别和速度整体规划。其中减速特征识别的任务是提前发现拐点，并计算通过该拐点的最大安全速度。整体速度规划处理是根据车子的约束条件，对各段进给速度进行整体规划，再配合运动控制卡提供的段内加减速控制，可以使机床保持高速平稳运行。

2.2 减速特征识别

数学上通常用曲率表示曲线的弯曲变化程度，由多段线段连接成的轨迹在段间连接点处仅仅是0阶连续，不可能直接计算出曲率。任锟等人提出了使用三次多项式曲线拟合离散的点来求出哥哥衔接点处曲率的近似值。但当衔接点处方向变化很大时，这种方法的效果并不好。张得里等人提出在衔接点处假设一个虚拟圆弧，用该虚拟圆弧表示该点的曲率半径。

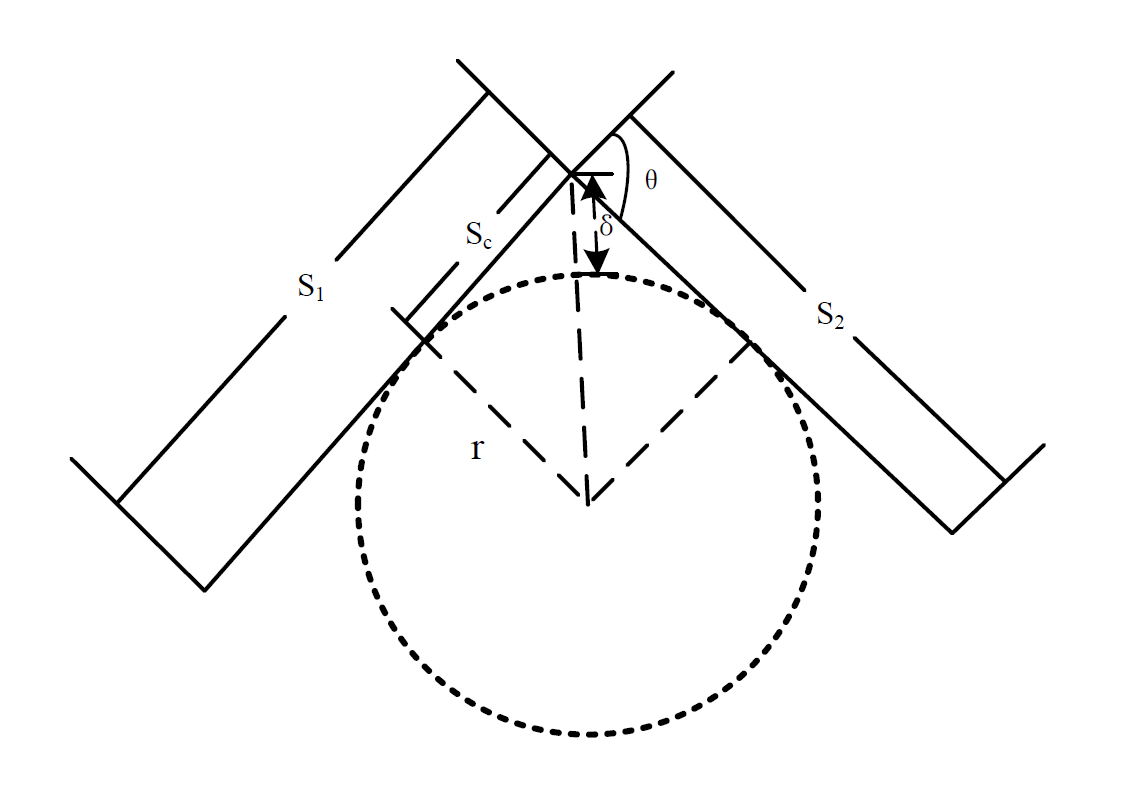
图1 直线段于直线段之间的虚拟圆弧

图1为直线段和直线段连接的情况。虚拟圆弧分别和两端直线相切，$\delta$为最大轮廓误差，可以通过合适的δ控制曲率半径的大小控制曲率半径的大小：
$$\sin (\frac{\pi -\theta }{2})=\frac{r}{r+\delta }$$
则过渡段$S_c$的长度为：
$$S_c=r\times \tan (\frac{\theta }{2})$$
车辆在经过圆弧段时，进给法向加速度$V$和虚拟圆弧半径$r$之间应该满足如下关系：
$$a_n=\frac{V^2}{r}\le a_{Nmax}$$
$$V_{Nmax}=\sqrt{a_{Nmax}\times r}$$
最终车辆的控制速度为：
$$V=\min (V^{\prime },V_{max},V_{Nmax})$$
其中$V_{max}$为最大允许前进速度，$a_{Nmax}$为最大法向加速度。

2.3 整体速度规划

当路径中的某段线段的起点和终点均为高曲率点时，器允许运行速度均很小，若以两者之间的最小速度作为直线段的运行速度，将大大降低车辆的运行速度。以直线加减速为例，按$a_{max}$进行加减速，则该段内能实际达到的最大速度$V_m$为

$$V_m=\min (\sqrt{\frac{V_i^2+V_{i+1}^2+2a_{max}\times S_i}{2}},V_{max})$$
设第$i$段长度为$S_i$则起点速度为$V_i$和终点速度为$V_{i+1}$需满足如下约束：
$$\frac{|V_i^2-V_{i+1}^2|}{2S_i}\le a_{max}$$
如果$V_i>V_{i+1}$, 此段为减速段，则以$V_{i+1}$为基准计算起点的最大进给速度$V_{i,max}$
$$V_{i,max}=\sqrt{V_{i+1}^2+2a_{i,max}{S}_i}$$
取
$$V_i=\min (V_i,V_{i,max})$$
如果$V_i<V_{i+1}$, 此段为加速段，则以$V_{s}i$为基准计算起点的最大进给速度$V_{i+1,max}$
$$V_{i+1,max}=\sqrt{V_i^2+2a_{i,max}{S}_i}$$
取
$$V_{i+1}=\min (V_{i+1},V_{i+1,max})$$
整个算法流程图如图2所示：

图2 进给速度整体规划处理算法示意图

参考文献

[1] 李建华. 基于 Look-Ahead 技术的 CNC 轨迹规划的研究[D]. 哈尔滨工业大学, 2008.
[2] 任锟, 傅建中, 陈子辰. 高速加工中速度前瞻控制新算法研究[J]. 浙江大学学报: 工学版, 2006, 40(11): 1985-1988.
[3] 刘青山, 高霖. 基于运动控制卡的 PC 数控进给速度前瞻控制[J]. 机械科学与技术, 2009, 28(9): 1194-1197.
[4] 游达章, 余炼, 张敏, 等. 嵌入式数控系统速度前瞻规划算法研究[J]. 兵器装备工程学报, 2020.
[5] Wang L, Cao J. A look-ahead and adaptive speed control algorithm for high-speed CNC equipment[J]. The International Journal of Advanced Manufacturing Technology, 2012, 63(5): 705-717.
[6] Hu J, Xiao L, Wang Y, et al. An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead[J]. The International Journal of Advanced Manufacturing Technology, 2006, 28(9): 930-935.