线性代数学习笔记11-1：总复习Part1（CR分解、LU分解、QR分解）

引用：MIT线性代数_2020年更新讲解课程

下面的一系列分解，涉及了线性代数中的各个重要知识点：

关于求解方程组的分解：

• Ch1[矩阵乘法角度] 满秩分解：$\mathbf{A}$=列满秩矩阵$\mathbf{C}$和行满秩矩阵$\mathbf{R}$的乘积
• Ch2[消元解方程组] LU分解
• Ch3[施密特正交化] QR分解：将列向量线性无关的矩阵$\mathbf{A}$，转为正交矩阵$\mathbf{Q}$，且$\mathbf{R}$必为上三角阵

关于特征值/特征向量/奇异值的分解：

• Ch5[相似对角化] 得到特征值和特征向量后，矩阵$\mathbf{A}$相似于以特征值为对角元的对角阵$\mathbf{\Lambda }$
• Ch4[对称矩阵] 对称矩阵$\mathbf{S}$具有正交的特征向量，对角化得到$\mathbf{S}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^T$
• CH6[奇异值分解（“广义对角化”操作）] 任意矩阵可分解为$\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T$，其中$\mathbf{\Sigma }$中左上角的对角阵对应将行空间中的标准正交基映射到列空间的标准正交基（$\mathbf{A}{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i$，这类似于找出特征值和特征向量）；$\mathbf{\Sigma }$中其余部分为0元素，对应$\mathbf{A}$的零空间中的一组正交基

Ch1. 矩阵乘法与CR分解

矩阵向量乘法的理解

• 应该将矩阵向量乘法视为矩阵列向量的线性组合，从整体视角看乘法：$$\left[\begin{array}{lll}1& 4& 5\\ 3& 2& 5\\ 2& 1& 3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=x_1\left[\begin{array}{c}1\\ 3\\ 2\end{array}\right]+x_2\left[\begin{array}{c}4\\ 2\\ 1\end{array}\right]+x_3\left[\begin{array}{c}5\\ 5\\ 3\end{array}\right]$$
• 推论：$\mathbf{Ax}$的结果，一定位于列空间$C(\mathbf{A})$中（视为列向量的线性组合）；
  即使是$\mathbf{ABCx}$，也位于列空间$C(\mathbf{A})$中，因为可以视为$\mathbf{A}(\mathbf{BCx})$
  

应用：
当处理大型矩阵时，我们无法关注矩阵中的每一个元素，此时要做的就是采样
如果希望了解矩阵的列空间，一个自然的想法是直接对矩阵的列向量进行采样；
然而，更好的做法是随机采样：随机生成向量$\mathbf{x}$（其元素值随机），然后将$\mathbf{Ax}$的结果作为对矩阵列空间的一个随机采样（$\mathbf{Ax}$一定是列空间中的向量，并且是随机取的，能够更好的描述列空间）

列空间与秩

对于上述的矩阵向量乘法$\mathbf{Ax}$，尝试所有可能的$\mathbf{x}$，就是在尝试所有可能的列向量线性组合，由此能够得到列空间$C(\mathbf{A})$

• 矩阵$\mathbf{A}$的列空间$C(\mathbf{A})$(也称为值域Range)是矩阵列向量组张成的空间；
  矩阵$\mathbf{A}$的列秩=列空间$C(\mathbf{A})$的维数=列空间基向量个数=$\mathbf{A}$中无关的列向量个数

例如上面的矩阵 A = [ 1 4 5 3 2 5 2 1 3 ] \mathbf A=\left[145325213

\right] A= ​132​421​553​ ​只有一列、二列是无关的，而第三列是前两列之和
因此，$\mathbf{A}$的秩为2，对应$C(\mathbf{A})$是二维平面，列空间只有两个基向量（$\mathbf{A}$的第一、二列是列空间的一组基）；

• $\mathbf{A}$的秩$Rank(\mathbf{A})$=列秩=行秩
• 方阵$\mathbf{A}$不可逆$⟺$$\mathbf{A}$不满秩$⟺$$\mathbf{A}$的列向量组线性相关$⟺\mathbf{Ax}=0$有非零解$⟺$$\mathbf{A}$的零空间维度$n-r>0$
  ps. 向量组${\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_n$线性相关$⟺$$a_1{\mathbf{x}}_1+a_2{\mathbf{x}}_2+...+a_n{\mathbf{x}}_n=0$有非零解

CR分解/满秩分解（求矩阵列向量的最大无关组）

从矩阵$\mathbf{A}$的列向量组中，提取最大无关组，它们给出了矩阵列空间$C(\mathbf{A})$的一组基：
例如，矩阵 A = [ 1 4 5 3 2 5 2 1 3 ] \mathbf A=\left[145325213

\right] A= ​132​421​553​ ​中，前两列构成最大无关组：$\mathbf{C}=\left[\begin{array}{ll}1& 4\\ 3& 2\\ 2& 1\end{array}\right]$
那么，如何找出矩阵$\mathbf{A}$的列向量的最大无关组？或者说，如何找出列空间的一组基？
这需要CR分解

矩阵$\mathbf{A}$的满秩分解：$\mathbf{A}$=列满秩矩阵$\mathbf{C}\times$行满秩矩阵$\mathbf{R}$
$$\mathbf{A}=\mathbf{CR}$$
例如 [ 1 4 5 3 2 5 2 1 3 ] = [ 1 4 3 2 2 1 ] [ 1 0 1 0 1 1 ] \left[145325213

\right]= \left[143221\right]\left[101011\right] ​132​421​553​ ​= ​132​421​ ​[10​01​11​]

其中：

• $\mathbf{C}$有$r$个列向量，即$\mathbf{A}$的列空间（$r$维）的一组基
  $\mathbf{R}$有$r$个行向量，即$\mathbf{A}$的行空间（$r$维）的一组基

注意，上面的$\mathbf{C}$完全取自$\mathbf{A}$中真实存在的列向量，而$\mathbf{R}$则不同：$\mathbf{R}$是行简化阶梯型
将$\mathbf{A}$的各列视为$\mathbf{C}$的列向量的线性组合，$\mathbf{R}$是相应的线性组合系数，则$\mathbf{R}$中必然含有单位阵${\mathbf{I}}_r$ ps. 不考虑列的出现顺序的问题
若希望$\mathbf{R}$也取自$\mathbf{A}$中真实存在的行向量，则需要将式子修正为$\mathbf{A}=\mathbf{CUR}$

• 理解1：$\mathbf{C}$的列向量为列空间的一组基，$\mathbf{R}$对这些列向量线性组合，表出$\mathbf{A}$的所有列（$\mathbf{R}$是行简化阶梯型）
• 理解2：$\mathbf{R}$的列向量为行空间的一组基，$\mathbf{C}$对这些行向量线性组合，表出$\mathbf{A}$的所有行

总结：

• CR分解给出了$\mathbf{A}$列空间/行空间的一组基；
  或者说给出了$\mathbf{A}$的列向量的最大无关组，并指出如何由无关组表出整个$\mathbf{A}$矩阵
• 实际上，CR分解，对应了将$\mathbf{A}$进行行初等变换，得到行简化阶梯型$\tilde{\mathbf{A}}$的过程（行简化阶梯型指出了$\mathbf{A}$的主元列，也即列向量的最大无关组）
• CR分解的推论：任意矩阵的秩=行秩=列秩（行空间的维数=列空间的维数）

证明：
$\mathbf{A}=\mathbf{CR}$中，$\mathbf{C}$可视为保留了$\mathbf{A}$列空间的一组基；$\mathbf{R}$可视为保留了$\mathbf{A}$行空间的一组基，根据矩阵乘法规则，$\mathbf{C}$的列数=$\mathbf{R}$的行数
这就是说，行空间和列空间维数相等，行秩=列秩

CR分解的问题：

• 难以处理，不是大型计算的最佳选择
• 当$\mathbf{A}$为可逆方阵，所有列线性无关（$\mathbf{C}$就是$\mathbf{A}$本身），此时$\mathbf{A}=\mathbf{CR}$变为$\mathbf{A}=\mathbf{AI}$（什么也没得到）

秩1矩阵=列向量乘以行向量

• 秩1矩阵的各行/各列 都是 第一行/第一列 的倍数；
• 秩1矩阵只有一个线性无关列向量，并且必然也只有一个线性无关的行向量（根据“行秩=列秩”的结论，这是显然的）

实际上，秩1矩阵是CR分解的特例：秩1矩阵=列向量$\times$行向量，秩=行秩=列秩=1

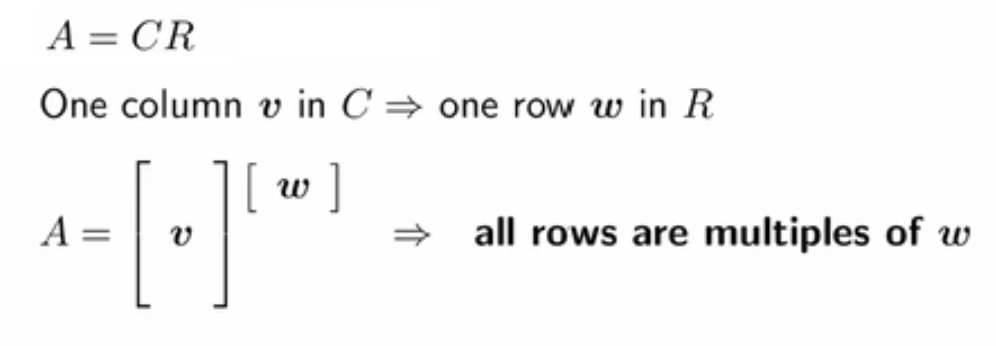
• 可见，列向量乘以行向量（外积），得到一个秩1矩阵

秩1矩阵是线性代数的基石Building Block，复杂的矩阵可以拆解为秩1矩阵

矩阵与矩阵乘法的理解：矩阵=秩1矩阵之和

通常将矩阵乘法理解为行向量乘以列向量

• 从“列向量乘行向量”入手，可将矩阵和矩阵的乘法视为一系列秩1矩阵的叠加
  $$\mathbf{AB}=\sum _{i=1}^n\mathbf{A}的第i列\times \mathbf{B}的第i行$$（求和的每一项为一个秩1矩阵）
  这是看待矩阵和矩阵乘法的全新视角！！！
  

下面介绍五个关键的矩阵分解时，均会使用这种“列向量乘行向量”的视角来进行解释。
后面将看到，这个视角也能解释LU、QR分解中为什么都出现了上三角矩阵

Ch2. 解方程组、LU分解与四个子空间

先研究齐次方程组$\mathbf{Ax}=0$，再研究非齐次方程组$\mathbf{Ax}=\mathbf{b}$

消元法与LU分解

LU分解来源于使用高斯消元法解方程的过程

消元法解方程的过程如下：核心是不断减少某一行方程中的未知量个数

消元的所有操作，都可以用矩阵乘法LU来完美表示，这就是LU分解$\mathbf{A}=\mathbf{LU}$
ps. 如果矩阵可逆的，则消元的过程一切顺利，并且主元不为零
ps. 需要行交换时，变为$\mathbf{PA}=\mathbf{LU}$

上图不仅是消元的过程，也是矩阵分解为一系列秩1矩阵的过程（列向量*行向量），正是因为每次消元“带走”了一行，才导致$\mathbf{A}=\mathbf{LU}$的$\mathbf{U}$为上三角矩阵

四个子空间

对于秩为r的m x n 矩阵$\mathbf{A}\in {\mathbb{R}}_r^{m\times n}$，有四个基本的子空间

• 列空间$C(\mathbf{A})$上面已经介绍过，维度$r$
• 行空间$C({\mathbf{A}}^T)$，维度$r$（因为行秩=列秩，这在CR分解部分证明过）
• 零空间$N(\mathbf{A})$：即$\mathbf{Ax}=0$所有可能的解$\mathbf{x}$构成的空间，维度$n-r$

为何零空间$N(\mathbf{A})$维度是$n-r$？
方程组$\mathbf{Ax}=0$看上去有$m$行方程，但其中真正独立、“起作用”的只有$r$个方程，剩余的$m-r$个方程都是有效方程的线性组合、是多余的；
$\mathbf{x}$有$n$个分量（未知数），这些未知数需要满足$r$个独立约束（有效方程数），可认为$r$个约束确定了$r$个分量，那么剩下的$n-r$个分量是自由变化的，即$\mathbf{Ax}=0$的零空间维度$n-r$
（对应消元后有$n-r$个自由列，即零空间的$n-r$个基向量）

• 左零空间$N({\mathbf{A}}^T)$：维数$m-r$

四个子空间的关系：

• 整个${\mathbf{R}}^n$空间，可拆分为$r$维行空间$C({\mathbf{A}}^T)$和$n-r$维零空间$N(\mathbf{A})$

为何行空间和零空间是一对？
因为对于$\mathbf{Ax}=0$，若$\mathbf{A}$的行向量有$n$个分量，则$\mathbf{x}$必也有$n$个分量（做矩阵向量乘法时维度对齐），故零空间和行空间都是${\mathbf{R}}^n$空间的子空间

• 行空间$C({\mathbf{A}}^T)$与零空间$N(\mathbf{A})$互为正交补

原因：
对于方程组$\mathbf{Ax}=0$，相当于$\mathbf{A}$的每一行与$\mathbf{x}$做点积，结果为0
这就是说，$\mathbf{A}$的任意行向量与$\mathbf{x}$正交，从而行空间与零空间正交

• 列空间$C(\mathbf{A})$与左零空间$N({\mathbf{A}}^T)$的关系和上面类似，等价于讨论${\mathbf{A}}^T$的行空间和零空间

由此，整个${\mathbf{R}}^n$空间和${\mathbf{R}}^m$空间，可以分别拆解为一对子空间；

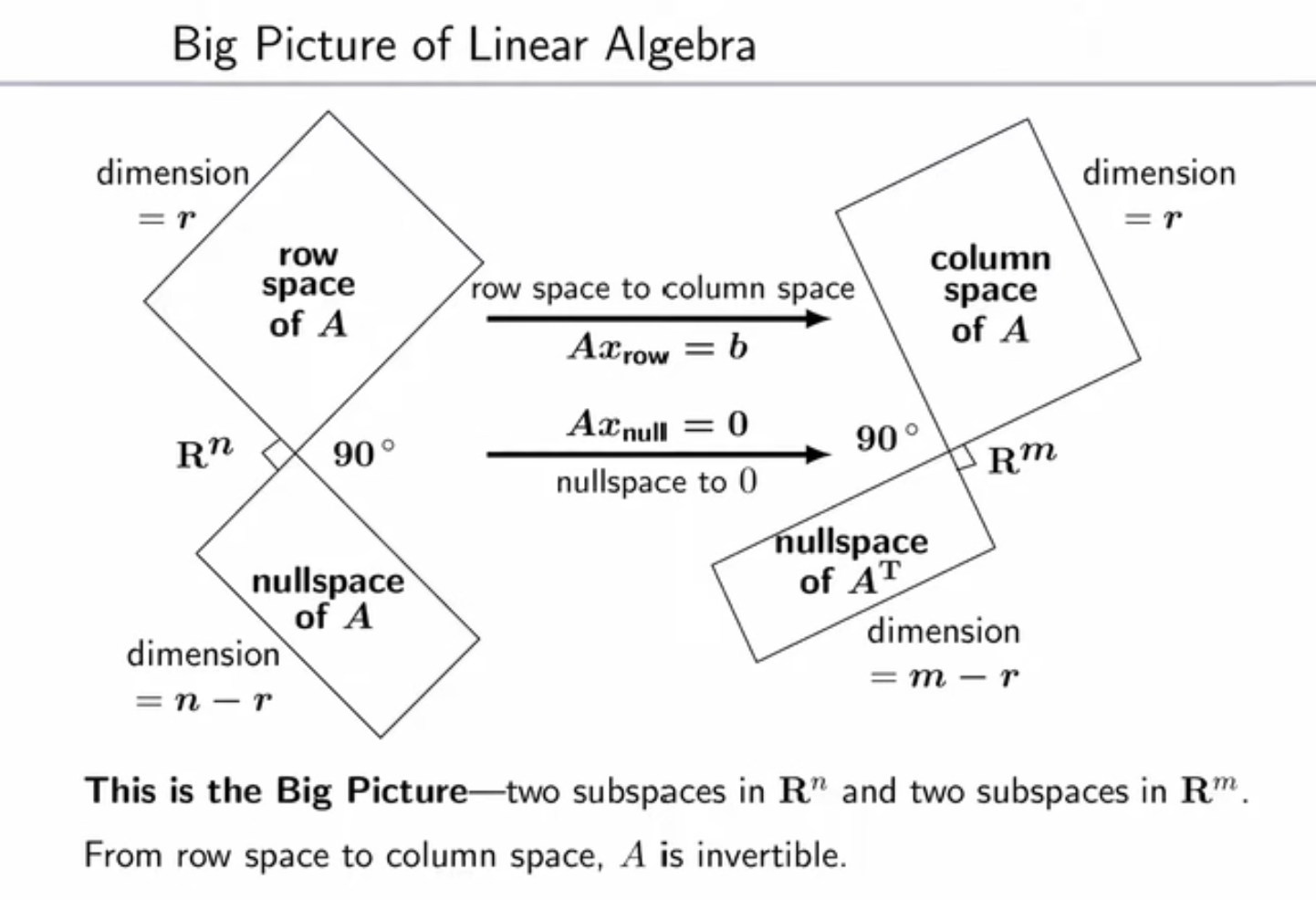
实际上，这两对子空间（行空间与零空间、列空间与左零空间）之间同样有联系：此时需要将$\mathbf{A}$视为一种映射算子，它将$n\times 1$向量$\mathbf{x}$映射为$m\times 1$向量$\mathbf{Ax}$（$\mathbf{Ax}$就是用行空间/零空间的向量${\mathbf{x}}_{row}$对$\mathbf{A}$的列向量做线性组合，结果位于列空间中）

• 对于行空间中的$\mathbf{x}$，$\mathbf{Ax}=\mathbf{b}$，这是将行空间投影到列空间
• 对于零空间中的$\mathbf{x}$，$\mathbf{Ax}=0$，这是将零空间投影到零向量（而不是左零空间）
• 将行空间投影到列空间$\mathbf{Ax}=\mathbf{b}$是可逆的，而$\mathbf{Ax}=0$则不可逆，这就是为什么说“零空间的存在（维度>0）会导致矩阵不可逆”，详见「伪逆」部分的笔记
  ps. 从另一个角度来验证：存在零空间，其维度$n-r>0$，即$n>r$不满秩，也就对应了不可逆

Ch3. 正交化、QR分解和最小二乘法

正交向量

正交Orthogonal可以理解为垂直Perpendicular的高级说法

向量的正交，就是内积为0：${\mathbf{x}}^T\mathbf{y}=0$
${\mathbf{x}}^T\mathbf{x}={\Vert \mathbf{x}\Vert }^2$ 则对应了向量本身模长的平方

正交矩阵

正交矩阵$\mathbf{Q}$的列向量构成一组标准正交基（各个基向量相互正交，模长为1）

正交矩阵$\mathbf{Q}$的性质：

• 正交矩阵$\mathbf{Q}$的逆矩阵${\mathbf{Q}}^{-1}={\mathbf{Q}}^T$
  原因：标准正交基满足${\mathbf{q}}_i^T{\mathbf{q}}_i=1，{\mathbf{q}}_i^T{\mathbf{q}}_j=0$ ，故正交矩阵$\mathbf{Q}$满足${\mathbf{Q}}^T\mathbf{Q}=\mathbf{Q}{\mathbf{Q}}^T=\mathbf{I}$

图中①为正交矩阵，有$\mathbf{Q}$满足${\mathbf{Q}}^T\mathbf{Q}=\mathbf{Q}{\mathbf{Q}}^T=\mathbf{I}$；
而②并不是真正的正交矩阵（只有两列，不是方阵），但由于各个列向量标准正交，仍有${\mathbf{Q}}^T\mathbf{Q}=\mathbf{I}$，而$\mathbf{Q}{\mathbf{Q}}^T\ne \mathbf{I}$
尽管如此，$\mathbf{Q}{\mathbf{Q}}^T$仍为一种投影矩阵（因为多次相乘，仍得到它本身）

• 将正交矩阵$\mathbf{Q}$视为线性变换，则几何意义是对原有基向量的旋转
  进而，两个正交矩阵的乘积${\mathbf{Q}}_1{\mathbf{Q}}_2$仍为正交矩阵
• 正交矩阵与其他向量相乘，不改变其长度
• 正交矩阵$\mathbf{Q}$特征值满足$|\lambda |=1$（可能为复数）

Gram-Schmidt正交化和QR分解

对于矩阵$\mathbf{A}$（前提：各个列向量线性无关），我们希望使其列向量${\mathbf{a}}_1...{\mathbf{a}}_n$变为正交的列向量${\mathbf{q}}_1...{\mathbf{q}}_n$，且各个列向量的模长标准化为1，这就是Gram-Schmidt正交化

用矩阵形式表达，就是QR分解$\mathbf{A}=\mathbf{QR}$，其中$\mathbf{R}={\mathbf{Q}}^T\mathbf{A}$为上三角阵

例如，原来的列向量${\mathbf{a}}_1=r_{11}{\mathbf{q}}_1$（第一个基向量，只需要标准化，$r_{11}=\Vert {\mathbf{a}}_1\Vert$）
而${\mathbf{a}}_2=r_{12}{\mathbf{q}}_1+r_{22}{\mathbf{q}}_2$（原来的第二个基向量，是标准化后的第一个/第二个基向量的线性组合）

仍然可以从秩1矩阵的角度入手，将QR分解进一步分解为若干秩1矩阵

最小二乘法：QR分解的主要应用

当$\mathbf{Ax}=\mathbf{b}$的方程个数过多时（$m>n$，行数大于未知量个数），意味着约束条件过多
此时，$\mathbf{A}$的列空间只是整个${\mathbf{R}}^m$空间中的一个平面，然而$\mathbf{b}$极有可能不在这个平面内，此时方程无解

我们将$\mathbf{b}$投影到$\mathbf{A}$的列空间内，从而寻找最优的近似解$\hat{\mathbf{x}}$（此时误差$\Vert \mathbf{e}{\Vert }^2=\Vert \mathbf{b}-\mathbf{A}\hat{\mathbf{x}}{\Vert }^2$最小）

• 可以体会到${\mathbf{A}}^T$矩阵的重要性：
  同时乘以${\mathbf{A}}^T$，能让$\mathbf{Ax}=\mathbf{b}$变得有解
  乘以${\mathbf{A}}^T$，任意矩阵$\mathbf{A}$变为方阵${\mathbf{A}}^T\mathbf{A}$（至少半正定）
• 若有$\mathbf{A}=\mathbf{QR}$，最小二乘法写为$\mathbf{R}\hat{\mathbf{x}}={\mathbf{Q}}^T\mathbf{b}$
  这就是说，将$\mathbf{A}$的列向量标准正交化后，求解最小二乘变得更加容易